Список терминов «сопротивления материалов»

ПРОГРАММА ПО СОПРОМАТУ

1. Введение. Цель и задачи курса. Основные гипотезы о деформируемом теле.

2. Понятие о напряженном и деформированном состоянии. Метод сечений.

3. Растяжение и сжатие.

3.1. Продольная сила. Напряжения в наклонных и поперечных сечениях.

3.2. Закон Гука. Три рода задач при расчете на прочность.

3.3. Статически неопределимые системы.

3.4. Механические свойства металлов при растяжении и сжатии.

4. Геометрические характеристики плоских сечений.

5. Теория напряженного и деформированного состояния. Обобщенный закон Гука.

6. Сдвиг. Расчет болтовых, заклепочных, шпоночных и сварных соединений на сдвиг, срез, смятие.

7. Гипотезы прочности.

8.1.Эпюры крутящих моментов. Касательные напряжения.

8.2. Расчет на прочность и жесткость при кручении.

9. Изгиб.

9.2. Расчет на прочность по нормальным напряжениям.

9.3. Касательные напряжения при изгибе. Формула Журавского.

10. Общие теоремы об упругих системах. Интеграл Мора и его вычисление по способу Верещагина и методом Симпсона - Карнаухова.

11. Сложное сопротивление.

11.1. Косой изгиб.

11.2 Внецентренное растяжение, сжатие стержня большой жесткости.

11.3. Сочетание изгиба с кручением.

11.4. Общий случай действия сил на брус круглого сечения.

12. Статически неопределимые системы. Метод сил.

13. Продольный изгиб прямого стержня. Формула Эйлера. Формула Ясинского.

14. Напряжения переменные во времени. Усталость. Выносливость.

15. Динамическая нагрузка. Удар. Колебание. Расчеты на прочность.

ВВЕДЕНИЕ

Что такое сопротивление материалов?

Любой студент второго и старших курсов высшего технического учебного заведения скажет, что это один из самых трудных предметов. Более того, процесс изучения и, особенно, сдачи экзамена по этому предмету у многих откладывается как одно из ярчайших воспоминаний всей жизни.

«Сдал сопромат – женись» – эту фразу знает любой студент-«технарь». Испокон века слагаются "правдивые" легенды о необычайной сложности и трудности изучения этого курса, хотя при ближайшем рассмотрении оказывается все не так сложно, если… Если хотя бы чуточку приложить усилия в изучении этой дисциплины, один раз понять и не запускать. Однако, "от сессии до сессии студенту живется весело", и, как правило, изучение "Сопротивления материалов" зачастую вызывает определенные трудности. Почему? Да потому, что курс "Сопротивление материалов" является практически первым прикладным инженерным курсом, с которым студент сталкивается в процессе обучения. Масса новых терминов, формул, понятий, способов и приемов описания состояния конструкций, которые до этого момента никогда не встречались, могут сбить с толка любого человека, какая бы "светлая" голова у него не была. Изучение курса "Сопротивление материалов" на первом этапе сродни с изучением иностранного языка. Именно поэтому курс "Сопротивление материалов" является гарантированным источником неудовлетворительных оценок и многочисленных пересдач экзаменов.

По прошествии многих лет бывшие студенты вспоминают экзамен по Сопромату как одно из самых запоминающихся событий их обучения в институте.

Как же возник курс сопротивления материалов? Прежде чем возводить какое-либо сооружение или строить машину, их надо спроектировать. В процессе проектирования необходимо выбрать материал и размеры каждой детали машины или сооружения так, чтобы при испытании и в эксплуатации она не разрушилась и не исказила сою форму. Для этого предварительно следует выявить характер и величины сил, воспринимаемых каждой деталью конструкции, и всесторонне изучить условия эксплуатации каждой детали для того, чтобы правильно выбрать подходящий материал. Зная характер внешней нагрузки и механические свойства материала, характеризующие деформацию и разрушение его под действием внешних сил, можно обратиться к определению размеров деталей машин или сооружений, которые обеспечили бы надежность в эксплуатации. при этом каждая деталь должна быть сконструирована так, чтобы затрачиваемый материал использовался наиболее рационально, т.е. детали должны быть по возможности легкими и дешевыми.

Требования надежности и наибольшей экономии, предъявляемые практикой к конструктору, противоречат друг другу. Первое требование ведет к увеличению расхода материала, второе – к его снижению.

Эти два противоречивых требования обусловили развитие расчетов на прочность деталей сооружений и машин, которые и составляют предмет сопротивления материалов.

Вначале элементарные расчеты на прочность излагались в курсах "Построение сооружений и машин". Они основывались на методах механики с учетом того, что все твердые тела деформируемы. Необходимость таких расчетов дала толчок к развитию механики деформируемого твердого тела. В дальнейшем, в связи с развитием техники, усложнением конструкций и расчетов, расчеты на прочность выделились в самостоятельный предмет "Сопротивление материалов", который изучается почти во всех высших технических учебных заведениях. Оказалось, что нет нужды говорить отдельно о деформации и прочности болтов, валов и т.п., поскольку элементы конструкций обычно можно схематизировать двумя формами стержня и оболочки (частный случай оболочки - пластина). Таким образом, "Сопротивление материалов" – общетехническая дисциплина, в которой на основе методов механики деформируемого твердого тела рассматриваются необходимые инженерам всех специальностей на жесткость и устойчивость элементов конструкций в форме стержней, пластин и оболочек, т.е. сопротивление материалов – введение в механику деформируемого твердого тела, необходимое инженерам.

В настоящее время в связи с увеличением размеров сооружений, созданием новых конструкций машин, летательных аппаратов, кораблей, повышением мощности агрегатов, увеличением скоростей подвижных частей машин, использованием высоких температур и давлений, применением новых материалов ответственность новых расчетов на прочность, а, следовательно, и важность курса «Сопротивление материалов» повышаются.

Каждый день практика ставит новые задачи и тем самым развивает механику деформируемого твердого тела и курс «Сопротивление материалов». Из года в год он насыщается новым содержанием.

ОБЩИЕ СВЕДЕНИЯ

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ,раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела – элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность, жесткость и устойчивость.

Прочность - свойство элемента конструкции не разрушаться под действием нагрузки.

Жесткость - способность элемента конструкции сопротивляться внешним нагрузкам в отношении деформации. Деформации не должны превышать допустимых величин.

Устойчивость - способность элемента конструкции сохранять под действием нагрузок первоначальную форму равновесия.

Напряжение, создаваемое в твердом теле внешними нагрузками, есть мера (с размерностью силы на единицу площади) интенсивности внутренних сил, действующих со стороны одной, мысленно отсекаемой, части тела на другую, оставшуюся (метод сечений). Внешние нагрузки вызывают деформацию тела, т.е. изменение его размеров и формы. В сопротивлении материалов исследуются соотношения между нагрузками, напряжениями и деформациями, причем исследования ведутся, с одной стороны, путем математического вывода формул, связывающих нагрузки с вызываемыми ими напряжениями и деформациями, а с другой – путем экспериментального определения характеристик материалов, применяемых в строениях и машинах. По найденным формулам с учетом результатов испытания материалов рассчитываются размеры элементов строений и машин, обеспечивающие сопротивление заданным нагрузкам. Сопротивление материалов не относится к точным наукам, так как многие его формулы выводятся на основе предположений о поведении материалов, которые не всегда точно выполняются. Тем не менее, пользуясь ими, грамотный инженер может создавать надежные и экономичные конструкции.

С сопротивлением материалов тесно связана математическая теория упругости, в которой тоже рассматриваются напряжения и деформации. Она позволяет решать те задачи, которые с трудом поддаются решению обычными методами сопротивления материалов. Однако между сопротивлением материалов и теорией упругости нет четкой границы. Хотя почти все задачи о распределении напряжений решены методами математического анализа, при сложных условиях эти решения требуют трудоемких выкладок. И тогда на помощь приходят экспериментальные методы анализа напряжений и созданные на их основе гипотезы (другими словами допущения), применяемые в сопротивлении материалов.

Основные гипотезы сопротивления материалов.Подводя итог данного раздела, перечислим основные гипотезы (принципы) о структуре и свойствах материалов, а также о характере деформаций.

1. Гипотеза о сплошности материала. Предполагается, что материал сплошной.

2. Гипотеза об однородности и изотропности.Предполагается, что материал однороден и изотропен.

3. Гипотеза о совершенной (идеальной) упругости материала. Все тела предполагаются абсолютно упругими. Эта предпосылка справедлива лишь при напряжениях, не превышающих для данного материала определенной. Постоянной величины, называемой пределом упругости σ_у.

4. Гипотеза о малости деформации. Деформации конструкции предполагаются настолько малыми, что можно не учитывать их влияние на взаимное расположение нагрузок и на расстояния от нагрузок до любых точек конструкции. На этом основании уравнения статики составляют для недеформированного тела.

5. Гипотеза о линейной зависимости между деформациями и нагрузками.Предполагается, что для большинства материалов справедлив закон Гука, устанавливающий прямопропорциональную зависимость между деформациями и нагрузками. Закон Гука справедлив лишь при напряжениях, не превышающих некоторого значения (предела пропорциональности σ_пр).

6. Принцип независимости действия и сложения сил (принцип суперпозиции).Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности. Этот принцип применим в случаях, когда могут быть использованы 4 и 5 гипотезы. Это же справедливо и в отношении деформаций.

7. Гипотеза плоских сечений (гипотеза Бернулли). Предполагается, что мысленно проведенные плоские сечения, перпендикулярные к оси стержня, в процессе его деформирования остаются плоскими и перпендикулярными к оси.

НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ

Виды напряжений.Самое важное понятие в сопротивлении материалов – это понятие напряжения как силы, действующей на малую площадку и отнесенной к площади этой площадки. Напряжения бывают трех видов: растяжения, сжатия и сдвига.

Если на металлическом стержне подвешен груз, как показано на рис. 1,а, то такой стержень называется растянутым или работающим на растяжение. Напряжение σ, создаваемое силой P в растянутом стержне с площадью поперечного сечения, равной A, дается выражением:

σ = P/A.

Если вес груза равен 50 000 Н, то растягивающая сила тоже равна 50000 Н. Далее, если ширина стержня равна 0,05 м, а толщина – 0,02 м, так что площадь поперечного сечения составляет 0,001 м², то растягивающее напряжение равно:

σ = 50 000/0,001 = 50 000 000 Н/м² = 50 МПа.

Растянутый стержень длиннее, чем до приложения растягивающих сил.

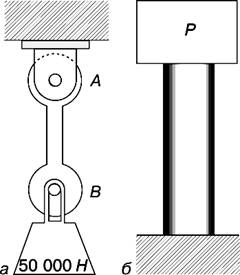
Рис. 1. РАСТЯНУТЫЙ (а) И СЖАТЫЙ (б) СТЕРЖНИ

Рассмотрим короткий цилиндр (рис. 1,б), на верхний торец которого положен груз. При этом во всех поперечных сечениях цилиндра действуют напряжения сжатия. Если напряжение равномерно распределено по всему сечению, то справедлива формула:

σ = P/A.

Сжатый цилиндр короче, чем в отсутствие деформаций.

Напряжение сдвига возникает, например, в болте (рис. 2,а), на котором верхним концом держится растянутый стержень AB с грузом 50 000 Н (рис. 1,а). Болт удерживает стержень, действуя с силой 50 000 Н, направленной вверх, на ту часть стержня, которая расположена непосредственно над отверстием в стержне, а стержень в свою очередь давит на среднюю часть болта с силой 50 000 Н. Силы, действующие на болт, приложены так, как показано на рис. 2,б. Если бы болт был сделан из материала с низким пределом прочности на сдвиг, например из свинца, то он был бы срезан по двум вертикальным плоскостям (рис. 2,в). Если же болт стальной и достаточно большого диаметра, то он не срежется, но в двух его вертикальных поперечных сечениях будут существовать напряжения сдвига. Если напряжения сдвига равномерно распределены, то они даются формулой:

τ_сд = P/A_сд.

Полная сила сдвига, действующая в каждом из поперечных сечений, равна 25 000 Н, и если диаметр болта равен 0,02 м (площадь поперечного сечения равна приблизительно 0,0003 м²), то напряжение сдвига τ_сд будет составлять 25 000 Н/0,0003 м², т.е. немногим более 80 МПа.

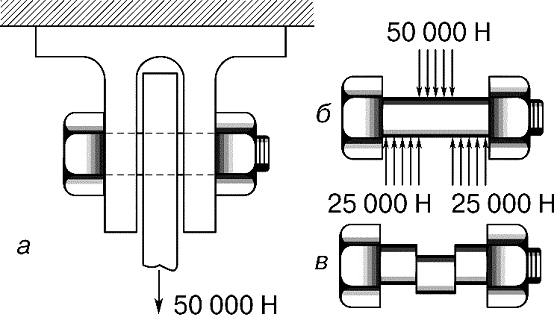
Рис. 2. НАПРЯЖЕНИЯ СДВИГА В БОЛТЕ

Напряжения растяжения и сжатия направлены по нормали (т.е. вдоль перпендикуляра) к площадке, в которой они действуют, а напряжение сдвига – параллельно площадке. Поэтому напряжения растяжения и сжатия называются нормальными, а напряжения сдвига – касательными.

Деформация.Деформацией называется изменение размера тела под действием приложенных к нему нагрузок. Деформация, отнесенная к первоначальному (до деформирования) размеру, называется относительной. Если изменение каждого малого элемента длины тела одинаково, то относительная деформация называется равномерной. Относительную деформацию часто обозначают символом e, а абсолютную (полную) – символом D. Если относительная деформация постоянна по всей длине L, то:

e = D/L.

Например, если длина стального стержня до приложения растягивающей нагрузки равна 2,00 м, а после нагружения – 2,0015 м, то полная деформация D равна 0,0015 м, а относительная – e = 0,0015/2,00 = 0,00075 (м/м).

Почти для всех материалов, применяемых в строениях и машинах, относительная деформация пропорциональна напряжению, пока оно не превысит т.н. предела пропорциональности. Это очень важное соотношение называется законом Гука. Оно было экспериментально установлено и сформулировано в 1678 году английским изобретателем и часовых дел мастером Р.Гуком. Данное соотношение между напряжением и деформацией для любого материала выражается формулой

σ = Ee,

где E – постоянный множитель, характеризующий материал. Этот множитель называют модулем Юнга по имени Т.Юнга, который ввел его в 1802 году, или же модулем упругости. Из обычных конструкционных материалов наибольший модуль упругости у стали; он равен примерно 200000 МПа. В стальном стержне относительная деформация, равная 0,00075, из приводившегося ранее примера вызывается напряжением σ = Ee = 200 000´0,00075 = 150 МПа, что меньше предела пропорциональности конструкционной стали. Если бы стержень был из алюминия с модулем упругости около 70 000 МПа, то, чтобы вызвать ту же самую деформацию 0,00075, достаточно было бы напряжения немногим более 50 МПа. Из сказанного ясно, что упругие деформации в строениях и машинах очень малы. Даже при сравнительно большом напряжении 150 МПа из приведенного выше примера относительная деформация стального стержня не превышает одной тысячной. Столь большая жесткость стали – ее ценное качество.

Чтобы наглядно представить деформацию сдвига, рассмотрим, например, прямоугольную призму ABCD (рис. 3). Ее нижний конец жестко заделан в твердое основание. Если на верхнюю часть призмы действует горизонтальная внешняя сила F, она вызывает деформацию сдвига, показанную штриховыми линиями. Смещение D есть полная деформация на длине (высоте) L. Относительная деформация сдвига g равна D/L. Для деформации сдвига тоже выполняется закон Гука при условии, что напряжение не превышает предела пропорциональности для сдвига. Следовательно, τ_s = G_sg, где G_s – модуль сдвига. Для любого материала величина G_s меньше E. Для стали она составляет около 2/5 E, т.е. приблизительно 80 000 МПа. Важный случай деформации сдвига – деформация в валах, на которые действуют внешние скручивающие моменты.

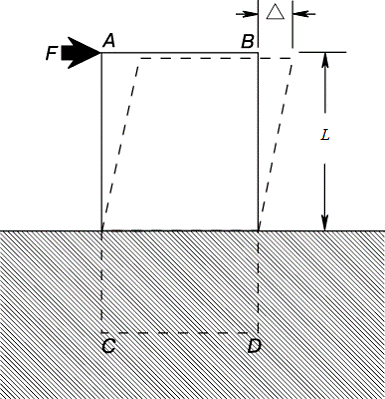
Рис. 3. ДЕФОРМАЦИЯ СДВИГА определяется как смещение Δ, отнесенное к исходной высоте L.

Выше речь шла об упругих деформациях, которые вызываются напряжениями, не превышающими предела пропорциональности. Если же напряжение выходит за предел пропорциональности, то деформация начинает расти быстрее, чем напряжение. Закон Гука перестает быть справедливым. В случае конструкционной стали в области, лежащей чуть выше предела пропорциональности, небольшое увеличение напряжения приводит к увеличению деформации во много раз по сравнению с деформацией, соответствующей пределу пропорциональности. Напряжение, при котором начинается столь быстрый рост деформации, называется пределом текучести. Материал, в котором разрушению предшествует большая неупругая деформация, называется пластичным.

Допускаемые напряжения

Допускаемое (допустимое) напряжение – это значение напряжения, которое считается предельно приемлемым при вычислении размеров поперечного сечения элемента, рассчитываемого на заданную нагрузку. Можно говорить о допускаемых напряжениях растяжения, сжатия и сдвига. Допускаемые напряжения либо предписываются компетентной инстанцией (скажем, отделом мостов управления железной дороги), либо выбираются конструктором, хорошо знающим свойства материала и условия его применения. Допускаемым напряжением ограничивается максимальное рабочее напряжение конструкции.

При проектировании конструкций ставится цель создать конструкцию, которая, будучи надежной, в то же время была бы предельно легкой и экономной. Надежность обеспечивается тем, что каждому элементу придают такие размеры, при которых максимальное рабочее напряжение в нем будет в определенной степени меньше напряжения, вызывающего потерю прочности этим элементом. Потеря прочности не обязательно означает разрушение. Машина или строительная конструкция считается отказавшей, когда она не может удовлетворительно выполнять свою функцию. Деталь из пластичного материала, как правило, теряет прочность, когда напряжение в ней достигает предела текучести, так как при этом из-за слишком большой деформации детали машина или конструкция перестает соответствовать своему назначению. Если же деталь выполнена из хрупкого материала, то она почти не деформируется, и потеря ею прочности совпадает с ее разрушением.

Запас прочности.Разность напряжения, при котором материал теряет прочность, и допускаемого напряжения есть тот «запас прочности», который необходимо предусматривать, учитывая возможность случайной перегрузки, неточностей расчета, связанных с упрощающими предположениями и неопределенными условиями, наличия не обнаруженных (или не обнаружимых) дефектов материала и последующего снижения прочности из-за коррозии металла, гниения дерева и пр.

Коэффициент запаса.Коэффициент запаса прочности какого-либо элемента конструкции равен отношению предельной нагрузки, вызывающей потерю прочности элемента, к нагрузке, создающей допускаемое напряжение. При этом под потерей прочности понимается не только разрушение элемента, но и появление в нем остаточных деформаций. Поэтому для элемента конструкции, выполненного из пластичного материала, предельным напряжением является предел текучести. В большинстве случаев рабочие напряжения в элементах конструкции пропорциональны нагрузкам, а поэтому коэффициент запаса определяется как отношение предела прочности к допускаемому напряжению (коэффициент запаса по пределу прочности). Так, если предел прочности конструкционной стали равен 540 МПа, а допускаемое напряжение – 180 МПа, то коэффициент запаса равен 3.

БАЛКИ

Балка – это длинный стержень с опорами и нагрузками, работающий в основном на изгиб. Поперечное сечение балки обычно одинаково по всей ее длине. Силы, с которыми опоры действуют на балку, называются реакциями опор. Наиболее распространены два вида балок: консольная (рис. 5,а) и балка с двумя опорами, называемая простой (рис. 5,б). Под действием нагрузок балка прогибается. При этом «волокна» на ее верхней стороне сокращаются, а на нижней – удлиняются. Очевидно, что где-то между верхней и нижней сторонами балки имеется тонкий слой, длина которого не изменяется. Он называется нейтральным слоем. Изменение длины волокна, расположенного между верхней (или нижней) стороной балки и ее нейтральным слоем, пропорционально расстоянию до нейтрального слоя. Если справедлив закон Гука, то напряжения тоже пропорциональны этому расстоянию.

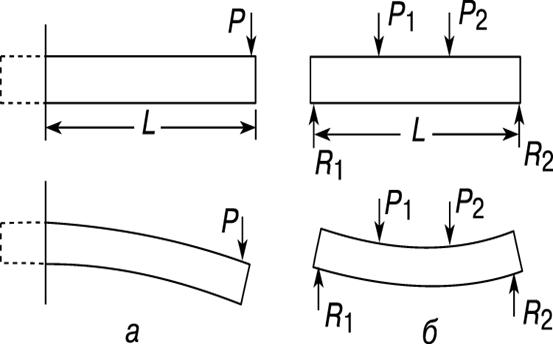
Рис. 5. ДВА ТИПА БАЛОК: а – консольная, б – простая. P, P1 и P2 – сосредоточенные нагрузки; R1 и R2 – реакции опор; L – длина.

Формула изгиба.На основе указанного распределения напряжений, дополненного условиями статики, выведена т.н. формула изгиба, в которой напряжение выражается через нагрузки и размеры балки. Она обычно представляется в виде^

σ = Mc/I,

где σ – максимальное напряжение в рассматриваемом поперечном сечении, c – расстояние от нейтрального слоя до наиболее напряженного волокна, M – изгибающий момент, равный сумме моментов всех сил, действующих по одну сторону от этого сечения, а I – момент инерции поперечного сечения (определенная функция формы и размеров последнего). Характер изменения нормальных напряжений в поперечном сечении балки показан на рис. 6.

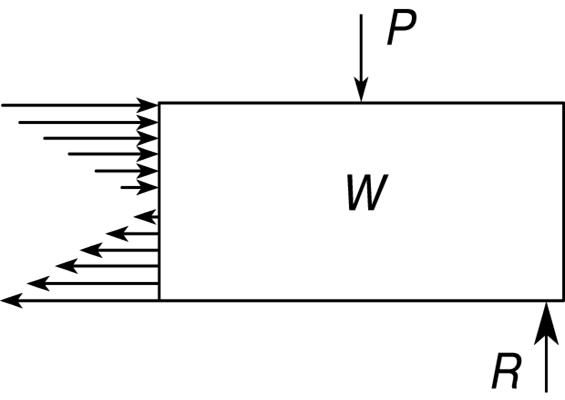
Рис. 6. РАСПРЕДЕЛЕНИЕ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ в поперечном сечении балки. P – нагрузка, R – реакция, W – вес (распределенная нагрузка).

В поперечных сечениях балок действуют также касательные напряжения. Их вызывает равнодействующая всех вертикальных сил, приложенных по одну сторону поперечного сечения горизонтальной балки. Сумма всех внешних сил и реакций, действующих на одну из двух частей балки, называется сдвигом в сечении балки и обычно обозначается через V. Касательные напряжения неравномерно распределены по сечению: они равны нулю на верхнем и нижнем краях сечения и почти всегда максимальны в нейтральном слое.

Прогиб балки.Часто требуется рассчитать прогиб балки, вызванный действием нагрузки, т.е. вертикальное смещение точки, лежащей в нейтральном слое. Это очень важная задача, поскольку прогиб и кривизну балки нужно знать при решении задач, относящихся к широкому кругу т.н. статически неопределимых систем.

Еще в 1757 году Л.Эйлер вывел формулу для кривизны изогнутой балки. В этой формуле кривизна балки выражается через переменный изгибающий момент. Чтобы найти ординату упругой кривой (прогиб), необходимо брать двойной интеграл. В 1868 году О.Мор (Германия) предложил метод, основанный на эпюрах изгибающих моментов. Этот графоаналитический метод имеет огромное преимущество перед прежними методами, так как позволяет свести все математические вычисления к сравнительно простым арифметическим выкладкам. Он дает возможность вычислять прогиб и наклон в любой точке балки при любой нагрузке.

Статически неопределимые балки.Многие балки, используемые в строениях и машинах, имеют более двух опор или только две опоры, но с заделкой одного из концов, исключающей возможность поворота. Такие балки называются статически неопределимыми, поскольку уравнений статики недостаточно для определения реакций в опорах и моментов в заделке. Чаще всего рассматриваются подобные балки трех типов: с одним заделанным (защемленным) концом и одной опорой, с заделанными обоими концами и неразрезные балки, имеющие более двух опор (рис. 7).

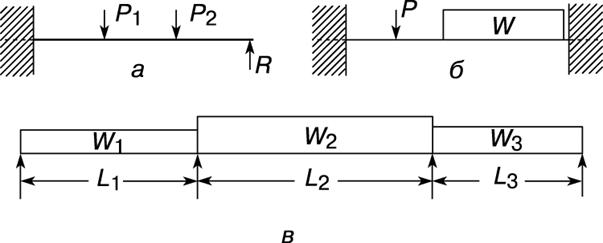
Рис. 7. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ БАЛКИ: а – с одним заделанным концом; б – с двумя заделанными концами; в – неразрезная трехпролетная. P, P₁, P₂ – сосредоточенные нагрузки; R – реакция; L₁, L₂, L₃ – длины; W, W₁, W₂, W₃ – веса (распределенные нагрузки).

Первое решение задачи о неразрезных балках было опубликовано французским инженером Б.Клапейроном в 1857 году. Он доказал т.н. теорему о трех моментах. Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид

M_AL₁ + 2M_B (L₁ + L₂) + M_CL₂ = – (W₁L₁³)/4 – (W₂L₂³)/4,

где - M_A, M_B и M_C – изгибающие моменты в трех опорах, L₁ и L₂ – длины левого и правого пролетов, W₁ – нагрузка на левый пролет, а W₂ – нагрузка на правый пролет.

Нужно написать такое уравнение для каждой пары смежных пролетов, а затем решить полученную систему уравнений. Если число пролетов равно n, то число уравнений будет равно n – 1.

В 1930 году Х.Кросс опубликовал свой метод расчета широкого круга статически неопределимых рам и неразрезных балок. Его «метод распределения моментов» позволяет обходиться без решения систем уравнений, сводя все вычисления к сложению и вычитанию чисел.

НАПРЯЖЕНИЕ ПРИ КРУЧЕНИИ

Если к концам вала приложены равные, но противоположно направленные внешние скручивающие моменты, то во всех его поперечных сечениях существуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. В круговом поперечном сечении вала деформации сдвига и касательные напряжения равны нулю в центре и максимальны на краю; в промежуточных точках они пропорциональны расстоянию от центра тяжести сечения. Обычная формула для максимального касательного напряжения при кручении такова:

τКРКккккКкКккк_кр= Tr/J_P,

где T (М_кр) – скручивающий момент на одном конце, r – радиус вала и J_P – полярный момент сечения. Для круга J = pr⁴/2.

Эта формула применима только в случае кругового поперечного сечения. Формулы для валов с поперечным сечением другой формы выводятся путем решения соответствующих задач методами математической теории упругости с привлечением в некоторых случаях методов экспериментального анализа.

СЛОЖНОЕ СОПРОТИВЛЕНИЕ

Нередко приходится рассчитывать балки, на которые в дополнение к поперечным нагрузкам действуют продольные силы растяжения или сжатия, приложенные к концам. В таких случаях напряжение в любой точке поперечного сечения равно алгебраической сумме нормального напряжения, создаваемого продольной нагрузкой, и изгибного напряжения, создаваемого поперечными нагрузками. Общая формула для напряжения в случае совместного действия изгиба и растяжения-сжатия такова: σ = ± (P/A) ± (Mc/I), где знак «плюс» относится к растягивающему напряжению.

Колонны

Каркасы зданий и фермы мостов состоят в основном из растянутых стержней, балок и колонн. Колонны – это длинные сжатые стержни, примером которых в каркасах зданий могут служить вертикальные стержни, несущие межэтажные перекрытия.

Если длина сжатого стержня более чем в 10–15 раз превышает его толщину, то под действием критических нагрузок, приложенных к его концам, он, потеряв устойчивость, изогнется, даже если нагрузки номинально приложены по его оси (продольный изгиб). Вследствие такого изгиба нагрузка оказывается внецентренной. Если эксцентриситет в среднем поперечном сечении колонны равен D, то максимальное сжимающее напряжение в колонне будет равно:

σ = (P/A) + (PDc/I).

Отсюда видно, что допускаемая нагрузка для колонны должна быть меньше, чем для короткого сжатого стержня.

Формулу для устойчивости гибких колонн вывел в 1757 году Л.Эйлер. Максимальная нагрузка P_кр (критическая сила), которую может нести гибкая колонна высотой L, равна

P_кр=π ²EI_min /(νL)²,

где ν – постоянный множитель, зависящий от конструкции основания (способа закрепления концов колонны), I_min – наименьший осевой момент инерции поперечного сечения.

Кроме критической силы, можно определить критическое напряжение:

σ_кр = π² Еi_min²/(νL)² = π² Е/λ²,

где i_min – минимальный радиус инерции поперечного сечения.

Отношение νL/i_min называется гибкостью λ (при продольном изгибе). Как нетрудно видеть, допускаемая нагрузка быстро убывает с увеличением гибкости колонны. В случае колонн с малой гибкостью формула Эйлера непригодна, и конструкторы вынуждены пользоваться эмпирическими формулами (например, формулой Ясинского).

В строениях часто встречаются внецентренно нагруженные колонны. В результате точного теоретического анализа таких колонн были получены «формулы секанса». Но расчеты по этим формулам весьма трудоемки, а потому часто приходится прибегать к эмпирическим методам, дающим хорошие результаты.

БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ

В задачах, о которых говорилось выше, рассматривались напряжения либо равномерно распределенные, либо линейно меняющиеся с удалением от нейтральной оси, где напряжение равно нулю. Однако во многих случаях закон изменения напряжения более сложен.

В качестве примера задач с нелинейным распределением напряжений можно привести искривленные балки, толстостенные сосуды, работающие под высоким внутренним или наружным давлением, валы некругового поперечного сечения и нагруженные тела с резкими изменениями поперечного сечения (канавками, буртиками и т.д.). Для таких задач рассчитываются коэффициенты концентрации напряжений.

Кроме того, выше речь шла только о статических нагрузках, постепенно прилагаемых и снимаемых. Переменные же и периодически меняющиеся нагрузки, многократно повторенные, могут приводить к потере прочности, даже если они не превышают статического предела прочности рассматриваемого материала. Такие отказы называются усталостными, а проблема их предотвращения приобрела важное значение в наш век машин и механизмов, работающих на необычайно высоких скоростях.

Рис. 1

Внутренние силы упругости определяют взаимодействие между частицами тела, расположенными по разные стороны от мысленно проведенного сечения. В разных сечениях тела возникают разные внутренние силы упругости, но по принципу действия и противодействия они всегда взаимны. Правая отсеченная часть тела действует на левую точно так же, как и левая на правую, а это означает, что равнодействующая внутренних сил может определяться из условий равновесия как левой отсеченной части тела, так и правой.

Из курса теоретической механики известно, что любую произвольную систему сил можно привести к центру тяжести сечения. В результате внутренние силы упругости, действующие в рассматриваемом сечении, приводятся к главному вектору R и главному моменту M. Выберем прямоугольную систему координат OXYZ так, что ось Z будет направлена по нормали к поперечному сечению, а оси Xи Y лежат в плоскости сечения. Проектируя главный вектор R на каждую из осей, а главный момент M на каждую из координатных плоскостей, получим шесть величин - 3 силы и 3 момента, - которые называются внутренними силовыми факторами (рис.2).

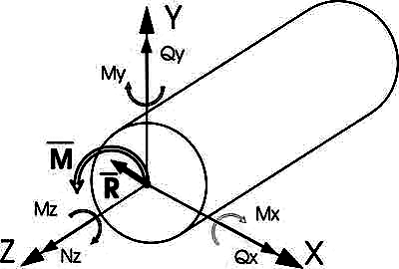Рис. 2

Полученные таким образом 6 внутренних силовых факторов (ВСФ) имеют строго определенные названия:

N_z- продольная (нормальная) сила;

Q_x, Q_y - поперечная (перерезывающая) сила;

M_x, M_y - изгибающий момент;

M_z - крутящий момент.

Иногда обозначение M_z заменяют на M_крили M_к, более точно отвечающие физическому смыслу этой величины.

График, показывающий как меняется внутренний силовой фактор по длине рассматриваемого тела, называется эпюрой.

Правильность построения эпюры обеспечивается, в первую очередь, надлежащим выбором характерных сечений, то есть тех сечений, в которых величина внутреннего силового фактора обязательно должна быть определена.

К характерным сечениям относятся:

1) сечения, расположенные бесконечно близко по обе стороны от точек приложения сосредоточенных сил и моментов;

2) сечения, расположенные в начале и в конце каждого участка с распределенной нагрузкой;

3) сечения, расположенные бесконечно близко к опорам, а также на свободных концах.

Виды сопротивлений

В зависимости от характера внешней нагрузки и от особенностей нагружаемого тела, в поперечных сечениях могут возникать не все шесть внутренних силовых факторов, а какой-либо один или некоторая их комбинация. В соответствии с этим различают следующие виды сопротивлений.

Растяжение (или сжатие) - это вид сопротивления, при котором во всех поперечных сечениях возникает только продольная сила N_z.

Кручение - это вид сопротивления, при котором во всех поперечных сечениях возникает только крутящий момент M_кр.

Чистый изгиб - это вид сопротивления, при котором во всех поперечных сечениях возникает только изгибающий момент M_x(или M_y). Чаще всего изгибающий момент M_x сопровождается наличием поперечной силы Q_y(или момент M_yсопровождается наличием поперечной силы Q_x). В этом случае имеет место поперечный изгиб.

Возможны случаи, когда в поперечных сечениях возникают два и более внутренних силовых фактора одновременно (исключая их комбинации, рассмотренные выше), тогда говорят о сложном сопротивлении..

Все перечисленные виды сопротивлений будут подробно рассмотрены в дальнейших разделах курса.

Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. При формировании расчетной схемы все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых наиболее часто встречаются: шарнирно-подвижная опора (возможные обозначения для нее представлены на рис.3,а), шарнирно-неподвижная опора (рис.3,б) и жесткое защемление, или заделка (рис.3,в).