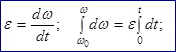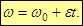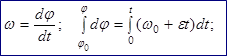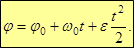Вращательное движение твердого тела. Линейная скорость. Векторная формула Эйлера.

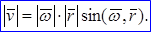Скорость точки при вращательном движении как векторное произведение –определяется выражением , которое описывает и величину, и направление скорости. Величина (модуль) этого векторного произведения: Таким образом:

Векторное произведение угловой скорости и радиус-вектора полностью определяет величину и направление скорости точки при вращательном движении.

Вращательное ускорение точки как векторное произведение –определяется выражением 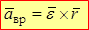, которое описывает и величину, и направление вращательного ускорения.

Величина (модуль) этого векторного произведения: Таким образом: .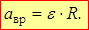

Направление вектора рассматриваемого векторного произведения можно установить по определению векторного произведения или по правилу правой руки.

Формулы Эйлера –с помощью раскрытия векторного произведения для скорости точки можно получить общие аналитические выражения для этой скорости через координаты рассматриваемой точки при произвольной расположении оси вращения в пространстве:

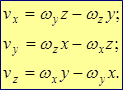
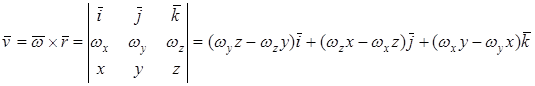
Отсюда получаются аналитические формулы для проекций скоростей точки:

60 Вращательное движение твердого тела. Ускорение точки.

Скорость точки при вращательном движении твердого тела :траектория точки известна (окружность радиуса R – расстояние точки до оси вращения), можно применить формулу для определения скорости точки при естественном задании движения: 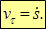. Дуговая координата связана с радиусом окружности: 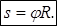.Тогда проекция скорости

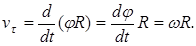на касательную к окружности: . Расчетной формулой является выражение для модуля скорости: .Вектор скорости направлен перпендикулярно радиусу в сторону дуговой стрелки угловой скорости. Как следует из формулы, скорость точки пропорциональна расстоянию ее до оси вращения (радиусу вращения).

Ускорение точки при вращательном движении твердого тела :траектория точки известна, можно применить

формулы для определения ускорений точки при естественном задании движения: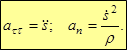

Тогда проекции ускорения на касательную к окружности и нормаль: 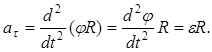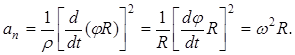. Расчетной формулой является выражение для касательного ускорения: . Вектор этого ускорения, называемого вращательным ускорениемнаправлен перпендикулярно радиусу в сторону дуговой стрелки углового ускорения.

Нормальное ускорение называется осестремительным ускорением 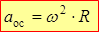, его направляют по радиусу к оси вращениянезависимо от направления дуговой стрелки угловой скорости.

Полное ускорение точки есть векторная сумма этих ускорений: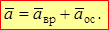

Угол между направлением полного ускорения и радиусом от величины радиуса не зависит и равен: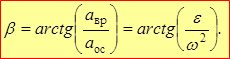

61 Равномерное и равнопеременное вращение.

Равномерное вращение – угловая скорость не изменяется по величине.

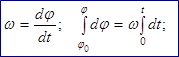
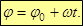
Равнопеременное вращение – угловое ускорение не изменяется по величине.