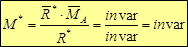Приведение произвольной системы сил к силе и паре сил ( основная теорема статики). Теорема Пуансо.
Пусть дана произвольная система сил (F1, F2,..., Fn). Сумма этих сил F=åFk - главный вектор системы сил. Сумма моментов сил относительно какого-либо полюса - главный момент рассматриваемой системы сил относительно этого полюса. Осн теор статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.
Пусть О — центр приведения, принимаемый за начало координат, r1,r2, r3,…, rn–соответствующие радиусы-векторы точек приложения сил F1, F2, F3, ...,Fn, составляющих данную систему сил (рис. 4.2, а). Перенесем силы F1, Fa, F3, ..., Fn в точку О. Сложим эти силы как сходящиеся; получим одну силу: Fо=F1+F2+…+Fn=åFk, которая равна главному вектору (рис. 4.2, б). При последовательном переносе сил F1, F2,..., Fn в точку О получаем каждый раз соответствующую пару сил (F1, F”1), (F2,F”2),...,(Fn, F"n).Моменты этих пар соответственно равны моментам данных сил относительно точки О: М1=М(F1,F”1)=r1 x F1=Мо(F1), М2=М(F2, F”2)=r2 x F2=Мо(F2), …, Мп=М(Fn, F"n)=rn x Fn=Мо(Fn). На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т. е. равен главному моменту, М0=М1+М2+...+Мn=Мо(F1)+Мо(F2)+…+ Мо(Fn)==åМо(Fk)=årk x Fk. Систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой Fo=åFk и парой сил с моментом M0=åM0(Fk)=årk x Fk.
24. Формулы для определения главного вектора и главного момента в декартовой системе координат.
Выбираем систему координатных осей Oxyz и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:
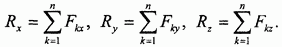
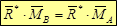
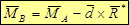По найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R . Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами: 
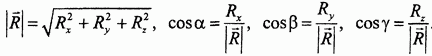Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента: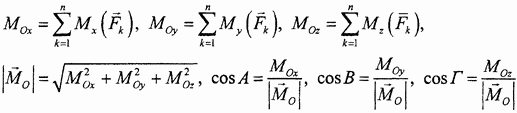 
Главный момент, по определению, есть векторная сумма моментов всех сил центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин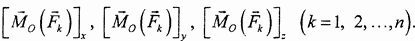 
Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:
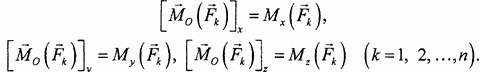
Косинус угла между главным вектором и главным моментом определяется так: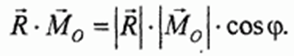 
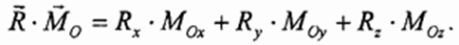Отсюда: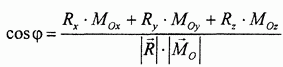 
25. Зависимость главного момента от выбора центра приведения.При переходе от одного центра приведения к другому изменяется момент произвольной силы Fi,выражения для моментов силы относительно каждого из центров: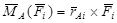 
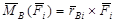
1. Между собой точки приведения A и B связаны радиус-вектором d: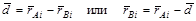 
2. Радиус-вектор rBiв выражение для момента силы MB(Fi):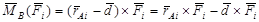 
3. Просуммируем моменты всех сил MB(Fi):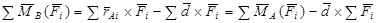 
4. Получили зависимость главного момента сил от выбора центра приведения: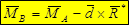 
главный минимальный момент выражается через скалярное произведение: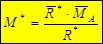 
Главный минимальный момент может быть вычислен как проекция главного момента в любой точке приведения на центральную ось: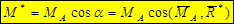 
26. Инварианты статики.
Инварианты системы сил –величины, не зависящие от выбора центра приведения:
Первый (векторный) инвариант – главный вектор системы сил R*: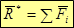 
Главный момент не является инвариантом, поскольку он зависит от выбора центра приведения. Однако существует величина, связанная с главным вектором, не зависящая от выбора центра приведения:
1. Запишем зависимость для главного момента системы от выбора точки приведения:
2. Умножим левую и правую части этого выражения скалярно на главный вектор и раскроем скобки:
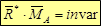
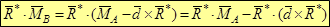3. Второе слагаемое в правой части обращается в ноль, т.к. главный вектор R* перпендикулярен вектору векторного произведения в скобках. Отсюда получаем тождество: Таким образом, скалярное произведение главного вектора R* на вектор главного момента MAесть второй (скалярный) инвариант: Отсюда, главный минимальный момент M* также является инвариантной величиной
