Главные оси и главные моменты инерции

Из формул (6.22) – (6.25) следует, что при повороте осей моменты инерции изменяются, но сумма осевых моментов остается постоянной.

Следовательно, если относительно одной оси значение момента инерции будет наибольшим, то относительно другой – наименьшим. В этом случае центробежный момент относительно этих осей оказывается равным нулю.

Главными центральными осями называются оси, проходящие через центр тяжести и относительно которых центробежный момент равен нулю, а осевые моменты относительно них (осей) обладают свойствами экстремальности и называются главными центральными моментами инерции. Относительно одной главной оси момент инерции имеет наименьшее значение – 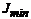, относительно другой – наибольшее .

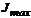Будем обозначать эти оси буквами u и v. Докажем приведенное утверждение. Пусть оси x и y – центральные оси несимметричного сечения (рис. 6.12).

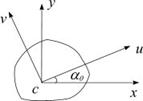
Рис.6.12

Определим положение главных осей путем поворота центральных осей на угол 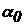, при котором центробежный момент становится равным нулю.

.

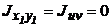Тогда из формулы (6.25)

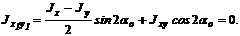
Откуда

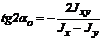. (6.26)

Формула (6.26) определяет положение главных осей, где 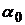– угол, на который нужно повернуть центральные оси, чтобы они стали главными. Отрицательные углы 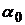откладываются по ходу часовой стрелки от оси x.

Теперь покажем, что относительно главных осей осевые моменты инерции обладают свойством экстремальности. Вычислим производную от выражения 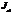(формула 6.22) и приравняем ее к нулю:

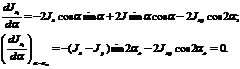(6.27)

Сравнивая выражения (6.27) с (6.25) устанавливаем, что

.

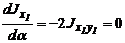Отсюда следует, что производная 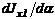обращается в нуль, когда 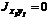, а это значит, что экстремальные значения имеют моменты инерции относительно главных осей u и v. Тогда по формулам (6.22) и (6.23):

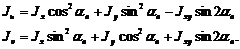(6.28)

По формулам (6.28) определяются главные центральные моменты инерции.

Если сложить почленно формулы (6.28), то, очевидно, 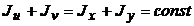. Если исключить из формул (6.28) угол 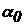, то получим более удобную формулу для главных центральных моментов инерции:

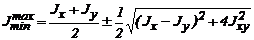. (6.29)

Знак «+» перед вторым слагаемым в (6.29) относится к 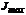, знак «-» – к .

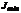Полезно иметь в виду частные случаи:

Если фигура имеет две оси симметрии, то эти оси являются главными центральными осями.

2. Для правильных фигур – равносторонний треугольник, квадрат, круг и т.п., имеющих более двух осей симметрии, все центральные оси являются главными, а моменты инерции относительно них равны между собой.

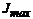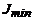Умение находить положение главных центральных осей и вычислять и необходимо для определения плоскости наибольшей жесткости сечения (след которой совпадает с осью 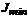) при расчетах на изгиб (глава 7).

35. Общий порядок определения главных центральных

Моментов.

Пусть требуется найти положение главных центральных осей и вычислить относительно них моменты инерции для плоского сечения, состоящего из швеллера и полосы (рис. 6.13):

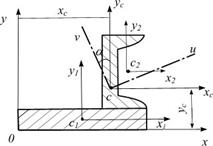
Рис. 6.13

Проводят произвольную систему координат xOy.

Разбивают сечение на простые фигуры и по формулам (6.5) определяют положение центра тяжести С.

Находят моменты инерции простых фигур относительно собственных центральных осей, используя сортамент или по формулам.

Через точку С проводят центральные оси x_c и y_c параллельно осям простых фигур.

Определяют моменты инерции простых фигур относительно центральных осей сечения, используя формулы параллельного переноса (6.13).

Определяют центральные моменты инерции всего сечения как сумму соответствующих моментов простых фигур, найденных в пункте 5.

Вычисляют угол 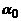по формуле (6.26) и, поворачивая оси x_c и y_c на угол 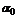, изображают главные оси u и v.

По формулам (6.29) вычисляют 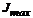и .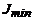

Делают проверку:

а) ;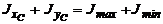

б) 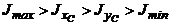, если ;

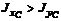в) .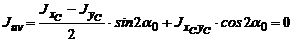

36) Общий прядок определения главных центральных моментов инерции. Пример:

1. Если фигура имеет две оси симметрии, то эти оси и будут ГЦО.

2. Для правельных фигур ( у которых больше 2- х оссей) все оси будут главными

3. Проводим вспомогательные оси(Х’ O’ Y’)

4. Разбиваем данное сечение на простые фигуры и показываем их собственные ЦО.

5. Находим положение ГЦО по формуле(21)

6. Вычисляем значения ГЦМ по формуле (23)

· Imax + Imin = Ix + Iy

· Imax >Ix>Iy>Iminесли Ix>Iy

· Iuv = Ix-Iy/2 sin2a + Ixycos2a +0

Формула 21:Tg2a = - 2Ixy/Ix - Iy

Формула23: Imax, Imin = *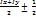

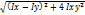
37) Изгиб. Классификация видов изгиба. Прямой и чистый изгиб. Картина деформирования балки. Нейтральный слой и ось. Основные допущения.

Изгиб – деформирование при котором в поперечном сечении возникает изгибающий момент Мх. Брус, который работает на изгиб-балка

Виды изгиба:

Чистый изгиб имеет место, если в сечении возникает только изгибающий момент

Поперечный изгиб- если одновременно с моментом возникает поперечная сила

Плоский - все нагрузки лежат в одной плоскости

Пространственный - если все нагрузки лежат в разных продольных плоскостях

Прямой - если силовая плоскость совпадает с одной из главных осей инерции

Косой - если силовая плоскость не совпадает ни с одной из главных осей

В результате деформирования на участке чистого изгиба можно видеть:

- продольные волокна искривляются по дуге окружности: одни- укорачиваются, другие-удлиняются; между ними есть слой волокон, которые не меняют своей длины- нейтральный слой (н.с.), линию его пересечения с плоскостью поперечного сечения называют нейтральной осью (н.о.)

-расстояние между продольными волокнами не меняется

-поперечные сечения, оставаясь прямыми, поворачиваются на некоторый угол

Допущения:

1.Оненадавливании продольных волокон друг на друга, т.е. каждое волокно находиться в состоянии простого растяжения или сжатия, что сопровождается возникновением нормальных напряжений Ϭ

2.О справедливости гипотезы Бернули, т.е. сечения балки, плоские и нормальные к оси до деформации, остаются плоскими и нормальными к ее оси после деформации