Последовательное соединение элементов

При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I= I₁=I₂

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: U= U₁+U₂+ U₃+U₄

А сопротивление R= R₁+R₂+R₃+R₄

U= U₁+U₂+ U₃+U₄= I₁R₁+ I₁R₂+ I₁R₃+ I₁R₄=I₁(R₁+R₂+R₃+R₄) = I₁R_экв .

P= I²R_экв

Смешанное соединение проводников— это такое соединение, при котором некоторые проводники соеденины последовательно, а некоторые — параллельно:

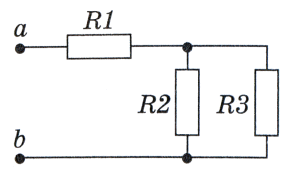
Чтобы найти силу тока, напряжение и сопротивление при смешанном соединении, нужно разбить его на простые участки, и найти силу тока, напряжение и сопротивление в них по вышеприведённым правилам, при этом схема упростится и найти в ней необходимые параметры не составит труда:

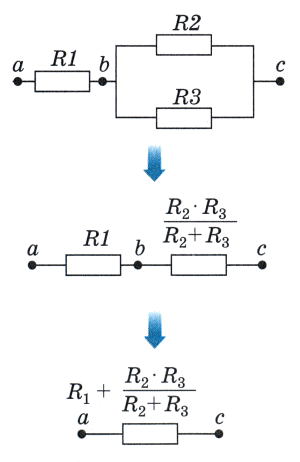
7. Метод эквивалентных преобразований (Метод свертки)

Суть метода : при последовательном соединении резисторов их сопротивления складываются R=R1+R2, при параллельном - складываются их проводимости g=g1+g2 (g1=1/R1,g2=1/R2). Источники э.д.с. с последовательно соединенными резисторами, заменяются на источники тока с параллельно соединенными резисторами согласно формулам:

Iрез.=E/R , Rрез.=R.

Верны и обратные преобразования,:

Ерез.=I*R , Rрез.=R.

Метод непосредственного применения законов Кирхгофа

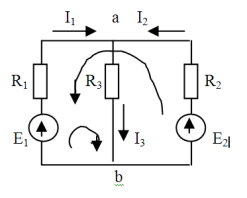
Задаемся условно положительным током в ветвях, затем составляем систему уравнений, равную числу неизвестных токов. По первому закону Кирхгоффа составляем (n-1) число уравнений, где n-число узлов, недостающее число уравнений составляем на основе 2го закона Кирхгоффа

I1 + I2 = I3

E1 = I1R1+ I3R3

E2 – E1 = I2R2 – I1R1

решая полученную систему, получим исходные токи

Метод наложения

В основе метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.

При расчете схемы, содержащей несколько ЭДС поочередно полагают равную нулю всей ЭДС кроме одной.

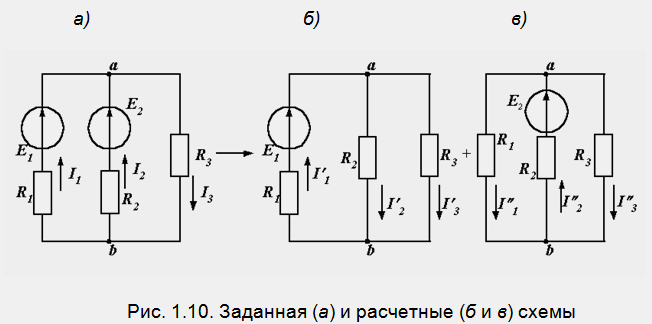
Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.

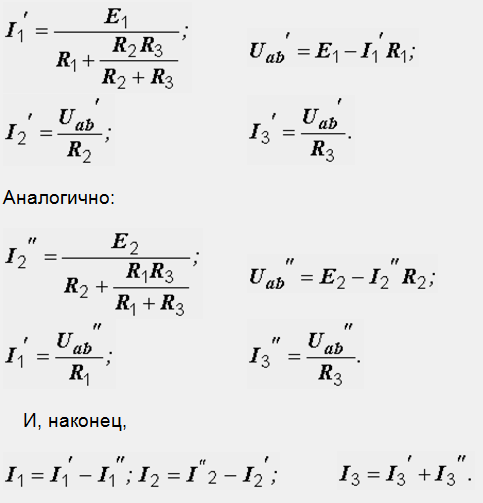
Метод контурных токов

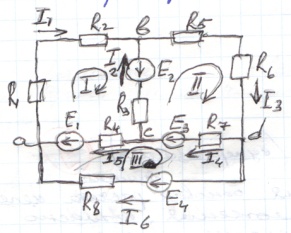При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа, тем самым ,сократив общее число совестно решаемых уравнений. Суть метода рассмотрим на примере:

Разбиваем схему на 3 смешных независимых контуров.Выбираем условно (+) направление обхода в них. В ветвях яв-ся общ для 2-х смежных контуров протекающие токи равны алгебр.сумме 2-х контурных токов. Применим для каждого контура в отдельности 2 закон Кирхгофа и получим систему уравнений равную числу контурных токов.

E₁+E₂=I_к1(R₁+R₂)+(I_к1-I_к2)R₃+(I_к1-I_к3)R₄

E₃-E₂=(I_к2-I₁)R₃+I_к2(R₅+R₆)+(I_к2-I_к3)R₇

E₄-E₁-E₃=I_к3R₈+(I_к3-I_к1)R₄+(I_к3-I_к2)R₇

Входящие в эти уравнения контурные токи удовлетворяют 1З.К. во всех точка разветвления. Полученные ур-я можно представить в виде более удобном для совместного решения:

E₁+E₂=I_к1(R₁+R₂+R₃+R₄)-I_к2R₃-I_к3R₄

E₃-E₂=-I_к1R₃+I_к2(R₃+R₅+R₆+R₇)-I_к3R₇

E₄-E₁-E₃=-I_к1R₄-I_к2R₇+I_к3(R₄+R₇+R₈)

Решая полученную систему рекомендуется метод Крамера. Найдем контурные токи по которым определим токи в ветвях

I₁=I_k1

I₂=I_k2-I_k1

I₃=I_k2

I₄=I_k2-I_k3

I₅=I_k1-I_k3

I₆=I_k3