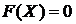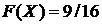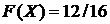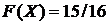Случайные величины и законы их распределения

Дискретные случайные величины

Ряд распределения и интегральная функция распределения дискретной случайной величины

С помощью интегральной функции распределения можно задать

1. дискретную случайную величину
2. непрерывную случайную величину
3. случайное событие
4. интервальную величину

	интервальными
	непрерывными
2. Случайные величины могут быть	дискретными
	точечными

3. Дискретные случайные величины:

1. число попаданий в мишень при десяти независимых выстрелах;
2. отклонение размера обрабатываемой детали от стандарта;
3. число нестандартных изделий, оказавшихся в партии из 100 изделий;
4. число очков, выпавших на верхней грани при одном подбрасывании игральной кости

4. Закон распределения вероятностей числа попаданий в мишень при двух независимых выстрелах, если вероятность попадания при каждом выстреле равна 0.8, имеет вид:

A.

X
p	0,14	0,16	0,64

B.

X
p	0,32	0,64

C.

X
p	0,8	0,16	0,8

D.

X
p	0,04	0,32	0,64

Монета подбрасывается 2 раза. Закон распределения случайной величины – числа появления орла.

A.

X
p	1/4	1/4	1/2

B.

X
p	1/2	1/4

C.

X
p	1/2	1/2

D.

X
p	1/4	1/2	1/4

6. Возможные значения случайной величины таковы: x₁=2, x₂=5, x₃=8. Известны вероятности первых двух возможных значений: p₁=0,4; p₂=0,15. Вероятность p₃:

A. 0,5

B. 1

C. 0,45

D. 0,4

7. В коробке 3 карандаша, из них 1 красный, 2синих. Извлекаются 2 карандаша. Закон распределения числа синих карандашей среди извлеченных:

A.

X
p	1/3	1/3	1/3

B.

X
p	2/3	1/3

C.

X
p		1/2	1/2

D.

X
p	1/3	1/3

8. Законы распределения дискретной случайной величины имеют вид:

A.

X
p	0,1	0,2	0,3

B.

X
p	0,2	0,4	0,3

C.

X
p	0,5	0,1	0,4

9. Дан закон распределения дискретной случайной величины:

X
p	0,3	0,1	P3

P₃ =…………

10. Способы задания дискретной случайной величины:

1. таблица распределения
2. многоугольник распределения
3. функция распределения вероятности
4. плотность распределения вероятности

С помощью ряда распределения можно задать

1. дискретную случайную величину
2. непрерывную случайную величину
3. случайное событие
4. интервальную величину

С помощью функции распределения можно задать

1. дискретную случайную величину
2. непрерывную случайную величину
3. случайное событие
4. интервальную величину

Закон распределения случайной величины X задан рядом распределения

Xi
Pi	9/16	6/16	1/16

Функция распределения при 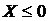примет значение

1. 
2. 
3. 
4. 
5. 

Закон распределения случайной величины X задан рядом распределения

Xi
Pi	9/16	6/16	1/16

Функция распределения при 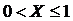примет значение

1. 
2. 
3. 
4. 
5. 

15. Дан закон распределения дискретной случайной величины:

X
p	P1	0,35	0,4	0,1

P₁ =…

16. Дан закон распределения дискретной случайной величины:

X
p	0,4	P2	0,15	0,1

Найти P₂ =…

17. Дан закон распределения дискретной случайной величины:

X
P	0,35	0,28	0,22	P4	0,01

P₄ =…

Ряд распределения дискретной случайной величины

xi
Pi	0,1	0,3	0,5

Недостающее значение равно….

19. Дан закон распределения дискретной случайной величины:

X
P	0,35	0,28	0,22	0,14	P5

P₅ =…

Пропущенное значение

Значения хi:
Вероятности р(хi)		1/6	1/6	1/6	1/6	1/6

1. 1/2
2. 1/4
3. 1/6
4. 1/8