Графиком функции называется множество точек плоскости с координатами (x, f(x))

Графиком функции называется множество точек плоскости с координатами (x, f(x))

Способы задания функции:

· аналитический способ (с помощью математической формулы);

· табличный способ (с помощью таблицы);

· описательный способ (с помощью словесного описания);

· графический способ (с помощью графика)

Функция называется четной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = f(x)

График четной функции симметричен относительно оси 0y

Функция называется нечетной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = –f(x)

График нечетной функции симметричен относительно начала координат.

Множество значений x называется областью определения функции (обозначается D(f))

Классы основных элементарных функций:

· Степенная функция ( 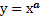, где а- действительное число)

· Показательная функция ( 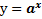, где a- положительное число, не равное 1)

· Логарифмическая функция (у= 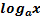, где а-положительное число, не равное 1)

· Тригонометрические функции (у=sinx, y=cosx, y=tgx,y=ctgx)

· Обратные тригонометрические функции( y= arcsinx, y=arccosx)

Производная функции в точке и на интервале, ее алгебраический, механический и геометрический смысл.

Если существует предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента 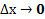, то он называется значением производной функции f(x) в точке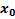

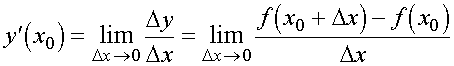
Если в точке x0 существует конечная производная функции y=f(x), то эта функция называется дифференцируемой в точке x0.

Если функция y=f(x) дифференцируема в каждой точке некоторого промежутка, то она дифференцируема на промежутке.

Алгебраический смысл: производная функции в точке есть угловой коэфициент касательной к графику этой функции

Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y=f(x) в точке x0 равен значению производной функции в этой точке.

Механический смысл: скорость тела равна первой производной координаты по времени:

V(t)=x / (t).

Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:

a(t)= V / (t)=x // (t).

Правила нахождения производных. Таблица производных. Производная

Сложной функции.

Правила нахождения производных

1. (с*u) ′=с*u′, с=const (постоянный множитель можно выносить за знак производной)

2. Производная суммы двух дифференцируемых функций равна сумме их производных:

(u 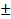v) ′ =u′ 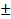v′

3. Производная произведения двух дифференцируемых функций вычисляется по следующему правилу: (uv) ′=u′v+uv

4. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:

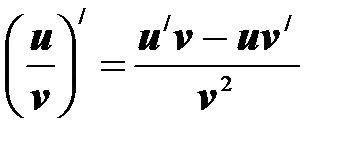
Таблица производных

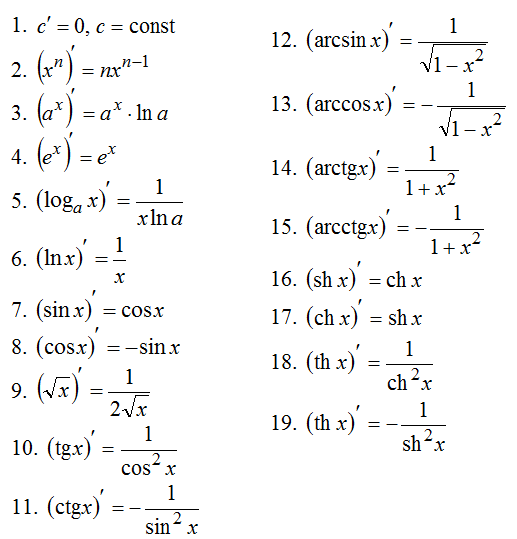
Производная сложной функции

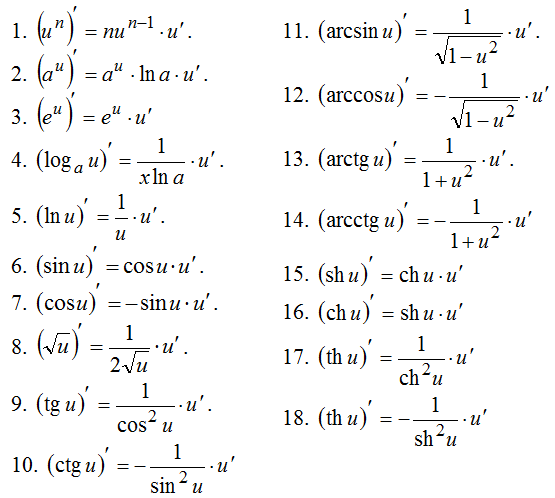
Дифференциал функции, его алгебраический и геометрический смысл.

Свойства дифференциала.

Горизонтальные асимптоты

Функции

Кривая называется выпуклой на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая называется вогнутой на интервале (а, b), если все ее точки лежат выше любой ее касательной на этом интервале

Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Схема исследования функции

1) Область определения функции.

Критические точки.

Построение графика.

Область значения функции.

Неопределенный интеграл, его свойства. Методы вычисления неопределенного интеграла: непосредственное интегрирование. Примеры.

Множество всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x)

Свойства:

1) Производная от неопределенного интеграла равна подынтегральной функции:

2) Дифференциал неопределенного интеграла равен подынтегральному выражению:

D ( ∫ f(x)dx)=f(x)dx

3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого С:

∫ df(x)=f(x)+C

Методы вычисления неопределенного интеграла: интегрирование методом подстановки. Примеры.

Основан на применении свойств интеграла F( 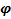(x))

Если функция f(t) имеет первооборазнуюF(t), а функция t= 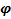(x) дифференцируема, то функция f(φ(x)) также имеет первообразную:

∫ f(φ(x))d(φ(x))-F(φ(x)+C

Примеры применения определенного интеграла для решения задач физики,

Химии, биологии

Стр. 73-77

Постоянными коэффициентами.

Дифференциальные уравнения в биологии, физике, химии. Примеры.

Cтр.105-109

Случайные события, их классификация. Примеры.

Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти.

Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие 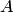— выпадание трех очков на первой игральной кости, событие 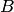— выпадание трех очков на второй кост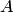и. и 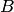— совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие 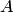— наудачу взятая коробка окажется с обувью черного цвета, событие 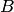— коробка окажется с обувью ко

ричневого цвета, 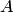и 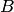— несовместные события.

Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.

Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.

Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.

События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.

Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. 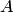— появление красного шара при одном извлечении, 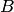— появление белого шара, 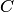— появление шара с номером. События 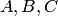образуют полную группу совместных событий.

Введем понятие противоположного, или дополнительного, события. Под противоположным событием 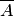понимается событие, которое обязательно должно произойти, если не наступило некоторое событие 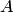. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие 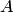, либо бракованным — событие .

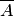20.Вероятность случайного события. Классическое определение вероятности. Свойства вероятности.

Свойства вероятности

Свойство 1. Если все случаи являются благоприятствующими данному событию 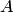, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления 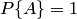, так как в этом случае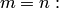

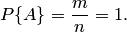
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию 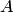, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления 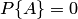, так как в этом случае :

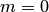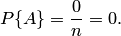
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.

Свойство 4. Вероятность наступления противоположного события 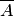определяется так же, как и вероятность наступления, события :

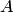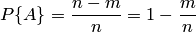
где 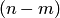— число случаев, благоприятствующих появлению противоположного события 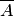. Отсюда вероятность наступления противоположного события 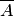равна разнице между единицей и вероятностью наступления события :

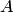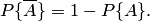
(1.2)

Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.

Формула Байеса

При выводе формулы полной вероятности предполагалось, что вероятности гипотез известны до опыта. Формула Байеса позволяет производить переоценку первоначальных гипотез в свете новой информации, состоящей в том, что событие произошло. Поэтому формулу Байеса называют формулой уточнения гипотез.

Теорема (Формула Байеса).Если событие может происходить только с одной из гипотез 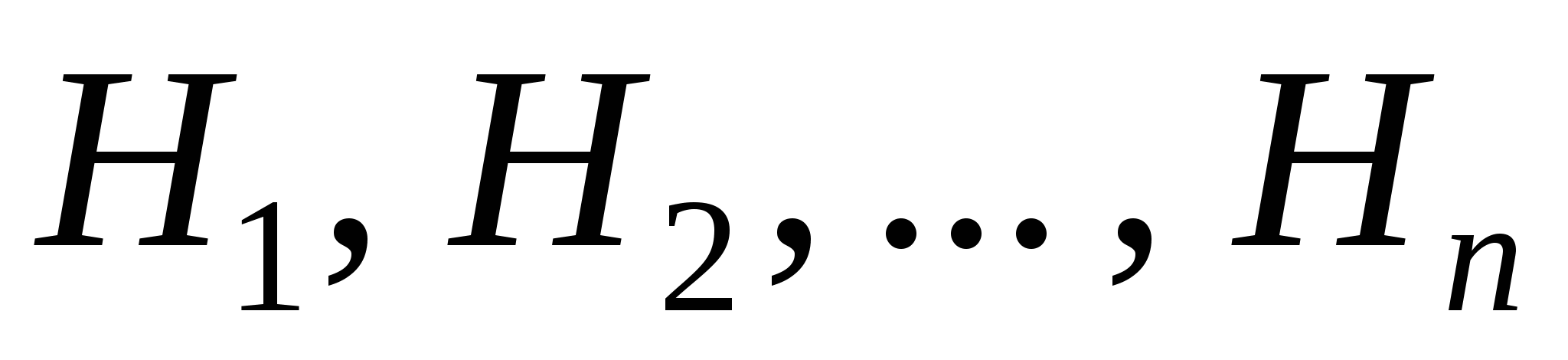, которые образуют полную группу событий, то вероятность гипотез при условии, что событие произошло, вычисляется по формуле

, .

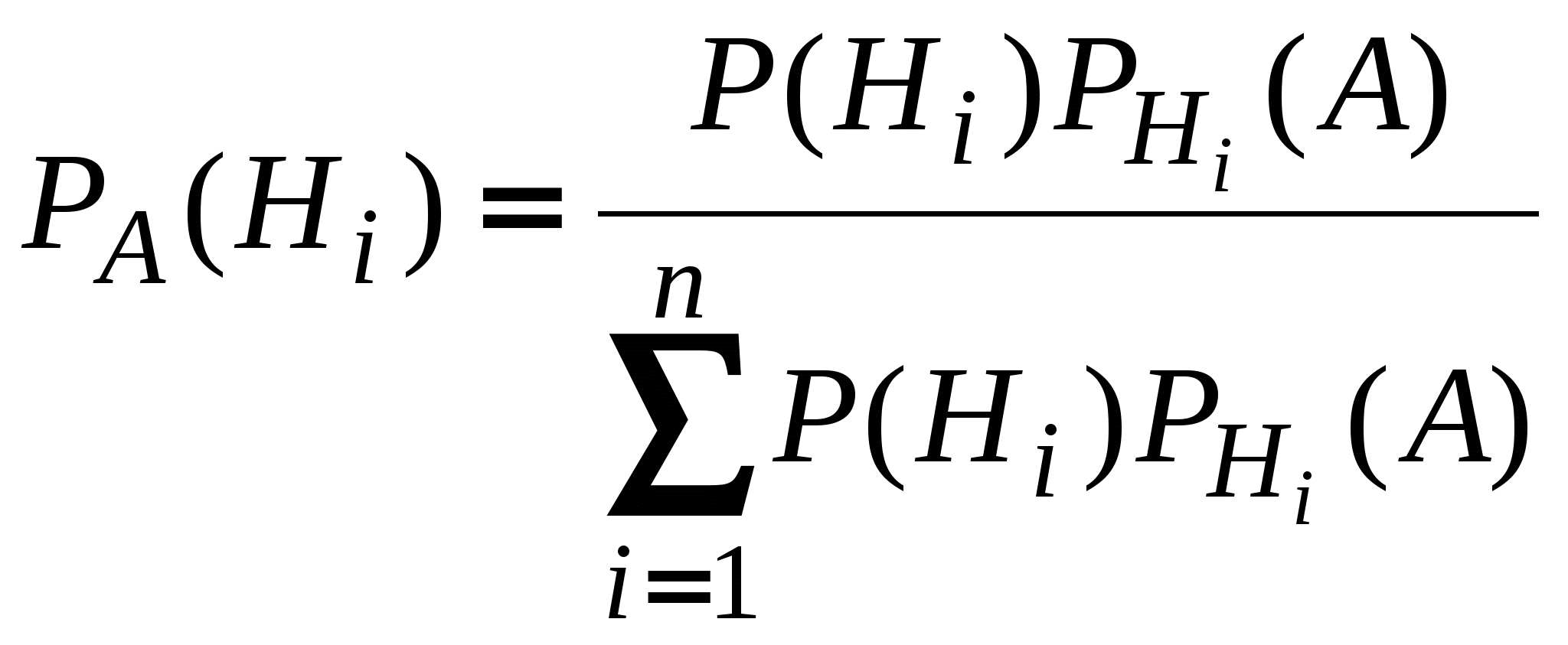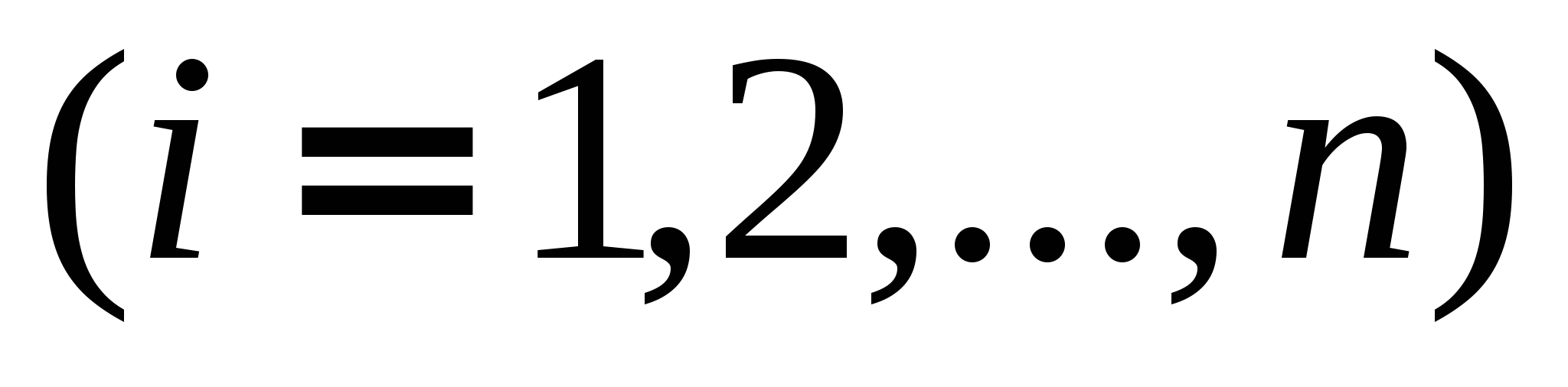Доказательство.

Формула Байеса или байесовский подход к оценке гипотез играет важную роль в экономике, т.к. дает возможность корректировать управленческие решения, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и.т.п.

Пример.Электролампы изготовляются на двух заводах. Первый завод производит 60% общего количества электроламп, второй – 40%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%. В магазин поступает продукция обоих заводов. Лампочка купленная в магазине оказалась стандартной. Найти вероятность того, что лампа изготовлена на первом заводе.

Запишем условие задачи, вводя соответствующие обозначения.

Дано:событие состоит в том, что лампа стандартная.

Гипотеза 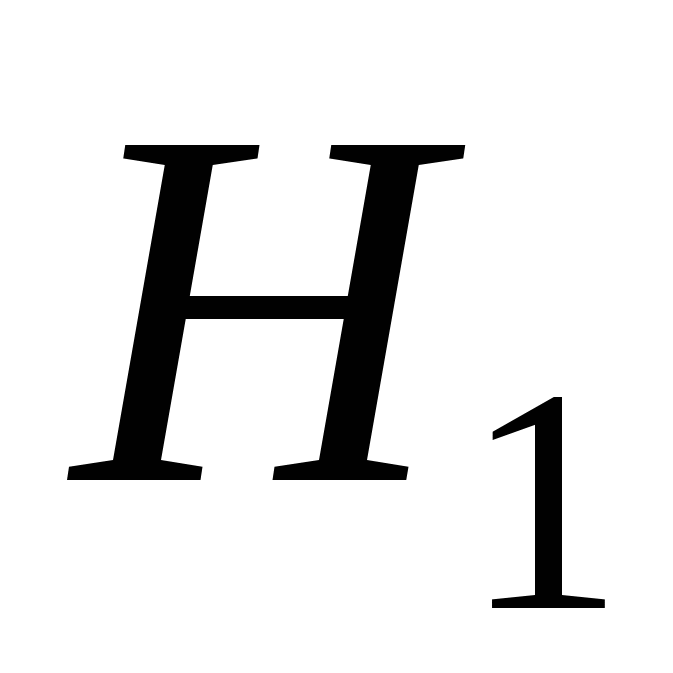состоит в том, что лампа изготовлена на первом заводе

.

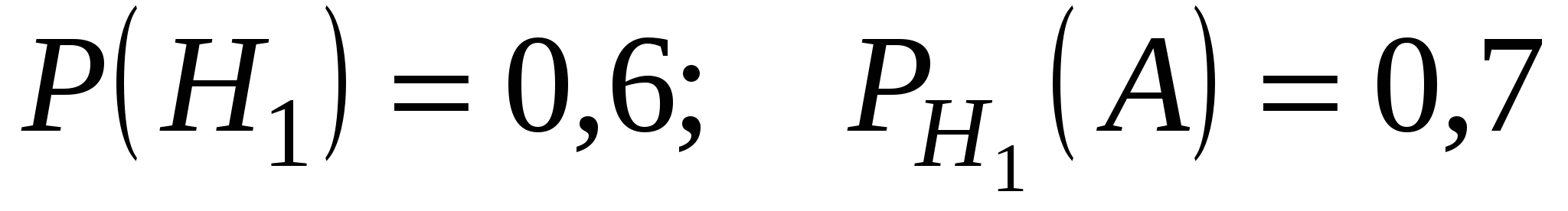Гипотеза 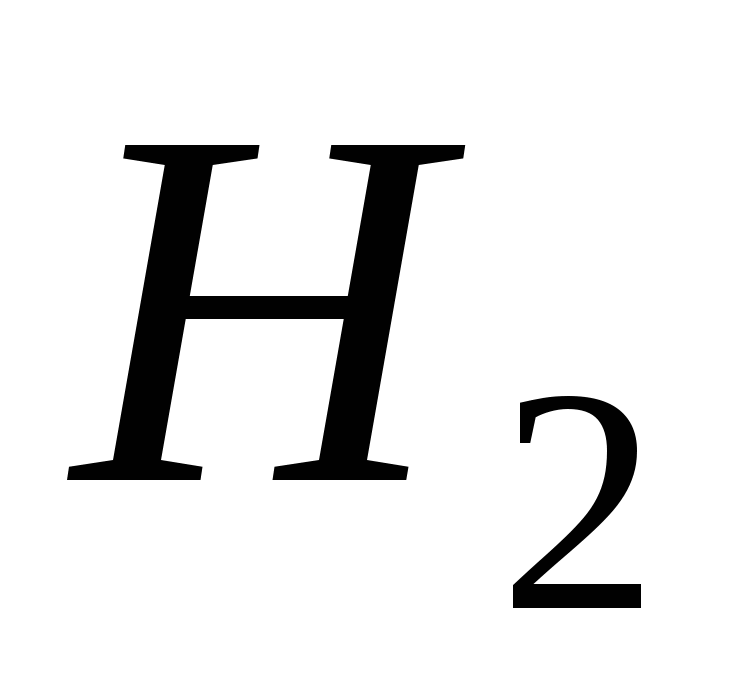состоит в том, что лампа изготовлена на втором заводе

.

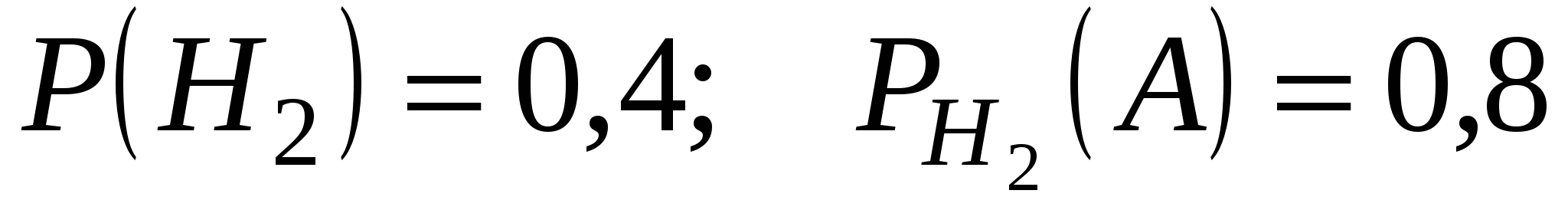
Формула Бернулли

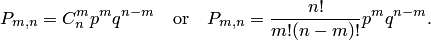
, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события, называютиспытаниями Бернулли, илисхемой Бернулли.

Графиком функции называется множество точек плоскости с координатами (x, f(x))

Способы задания функции:

· аналитический способ (с помощью математической формулы);

· табличный способ (с помощью таблицы);

· описательный способ (с помощью словесного описания);

· графический способ (с помощью графика)

Функция называется четной, если

– область определения функции симметрична относительно нуля

– для любого х из области определения f(-x) = f(x)