Монотонность функции. Достаточное условие возрастания (убывания) функции.

Убыв. и возраст. ф-ии назыв. монотонностью.

Достаточное условие возрастания(убывания): f(x) – возвраст. на Х, если для любых х1, х2 принадлеж. Х, х1<x2=>f(x1)<f(x2). f(x) – убыв. на Хó для любых х1,х2 принадлеж. Х, х1<x2=>f(x1)>f(x2).

Локальные экстремумы функции. Необходимое условие экстремума. Достаточное условие экстремума.

хо назыв. т. локального max f(x) если сущ. некот. окрестность Ve(xo), то для любых. х принадлеж. Ve(xo) x≠xo, f(xo)>f(x)

f(xo)<f(x), то xo – т. лок. min

Эти точки назыв. точками лок. экстремума, значение ф-ии в этих точках назыв экстремумами.

Необходимый признак экстремума: ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.

Достаточный признак: точка х₀ является точкой экстремума, если ее производная в этой точке меняет знак:

- если с “+” на “-”, то х₀- т. max

- если с “-” на “+”, то х₀- т. min

Наибольшее и наименьшее значение функции на отрезке.

Глобальный экстремум –наиб. и наим. знач. ф-ции на огран. замкнутом мн-ве.

1.Нахождение производной f’(x).

2.Решаем уравнение f’(x)=0, находим критические точки, в которых производная=0, или не существует.

3.Критическими точками разбиваем область определения на интервалы и определяем знак производной на каждом интервале. Если f’(x) меняет знак с + на - , то это точка max, если с – на +, то это точка min. Если производная не меняет знак, то функция f(x) в этой точке экстремума не имеет.

Выпуклость, вогнутость и точки перегиба графика функции.

Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках.

Линия наз-ся вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.

Признаки точки перегиба: чтобы X₀ была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х₀.

Асимптоты графика функции.

Прямая, к которой приближается график ф., но никогда не пересечёт её, называется асимптотой графика ф. Пусть y=kx+b называется асимптотой графика ф. f(x), при 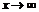, если 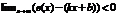. Коэффициент k и b вычисляются

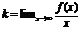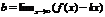; . Таким образом определяются горизонтальные и наклонные асимптоты. Чтобы определить вертикальную асимптоту, необходимо исследовать функцию в точке разрыва. Прямая x=a называется вертикальной асимптотой графика функции f(x), если 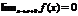или .

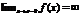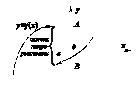
разрыв ф-ции первого вида

Свойства неопределенного интеграла.

1. (òf(х)dх)'= f(х)

2.dòf(х)dх)'=f(х)dх

3. òdF(х)=F(х)+С

4. òkf(х)dх=kòf(х)dх, k¹0.

5. ò(f(х)±g(х))dх= òf(х)dх±òg(х))

Таблица основных неопределенных интегралов.

1. ò0dх=С.

2. 2.òхdх= х+С.

3. 3. òх^adх= 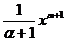+С, a¹1.

4. òсоsхdх=sinх+С; 5. òsinхdх= –соsх+С;

6. ò 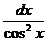=tgх+С; 7. ò 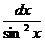=-сtgх+С;

8. ò 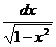= 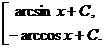; 8а. ò = ;

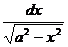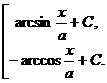9. ò 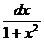= 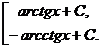; 9а. ò = ;

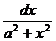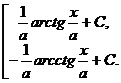10. òа^хdх= а^х/lnх+С; 10а. òе^хdх= е^х + С;

11. ò 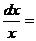ln|х|+С;12. ò 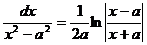+С; 13 ò 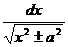=ln|х+ 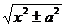|+С