Напряжение как мера внутренних сил.

Аксиомы статики

Аксиома инерции. Под действием уравновешенной системы сил материальная точка (тело) находится в состоянии покоя или движется равномерно и прямолинейно.

Аксиома равновесия двух сил. Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

Аксиома присоединения и исключения уравновешивающихся сил. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать от него уравновешенную систему сил.

Аксиома параллелограмма сил. Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту точку и равную их геометрической сумме.

Аксиома равенства действия и противодействия. Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

Аксиома о сохранении равновесия сил, приложенных к деформируемому телу. Равновесие деформируемого тела не нарушится, если это тело отвердеет.

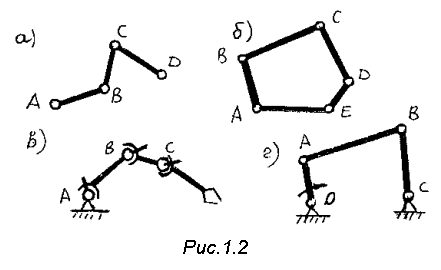
3.Кинематическая цепь - это система звеньев, образующих между собой кинематические пары. В зависимости от того, какие кинематические пары присутствуют в цепи и как они расположены, различают плоские и пространственные кинематические цепи. В плоской кинематической цепи все звенья движутся в одной или параллельных плоскостях (рис.1.2а.). Кинематическая цепь, звенья которой образуют замкнутый контур, называется замкнутой (рис.1.2б), если контур не замкнут, цепь называется незамкнутой или открытой (рис.1.2в). В традиционных механизмах обычно используются замкнутые кинематические цепи, незамкнутые цепи находят применение только в манипуляторах. Механизм – это кинематическая цепь, в которой указаны стойка, входные и выходные звенья.

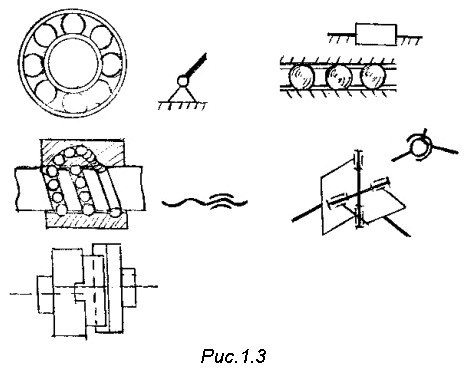
На основе кинематических цепей можно получать не только механизмы, но и устройства, заменяющие некоторые кинематические пары, так называемые кинематические соединения (рис.1.3). Шарико- или роликоподшипник эквивалентен вращательной паре. Роликовые направляющие заменяют поступательную пару. Винтовая пара качения заменяет обычную винтовую пару. Карданный шарнир, он же называется шарниром Гука или универсальным шарниром, заменяет сферическую пару с пальцем. Если вилку снабдить еще одной вращательной парой получим аналог сферической пары. Крестовое соединение допускает два поступательных движения без вращения.

Перемещения и деформации.

Под действием внешних сил реальное тело деформируется. При этом первоначальное положение его сечений изменяется. Перемещения сечений вдоль прямой линии называются линейными, а перемещения, вызывающие поворот линий и плоскостей, - угловыми.

Деформация – характеристика интенсивности изменения линейных и угловых перемещений. Коэффициент податливости численно равен удлинению (упрочнению) бруса, вызванному силой, равной единице силы (1 Н или 1 кН). Если деформации тела исчезают после его разгрузки, их считают упругими, а неисчезающие деформации называют остаточными или пластическими.

На поверхности тела некоторой точки прямой l, образующей отрезки АВ и ВС, после нагружения тела силами F1, F2, F3, деформируются, изменяются, а отрезки удлиняются на .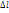

Предел отношения приращения длины отрезка его первоначальной длине называется относительной линейной деформацией.

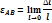
Деформация направляющих координатных осей обозначается соответствующими индексами( )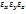

Предел разности углов ABC и A’B’C’

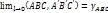- угловая деформация(угол сдвига) в т.В плоскости АВС.

В координатных плоскостях углы сдвига: ,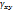

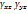
Т.о. в общем случае в точке имеют место 3 линейных и 3 угловых деформации.

Совокупность линейных и угловых деформаций по различным плоскостям, проходящих через данную точку, характеризуют деформирование состояния тела в этой точке.

Профильные соединения.

Профильные соединения прим для передачи вращ М от вала к ступице. В профильных соединениях контакт вала и ступицы осущ по некруглой поверхности. Профсоед имеют в поперечном к оси соединения сечении плавный некруглый профиль поверхности контакта вала и ступицы. Чаще прим равноосныесоедтреуг профиля. Прим-ый профиль обладает св-ом равноосности – постоянством диаметрального размера. Профсоед в осевом направлении могут быть цилиндрическими или коническими (фасонно-профсоед-ия: а — по цилиндр пов, б — по коничпов.).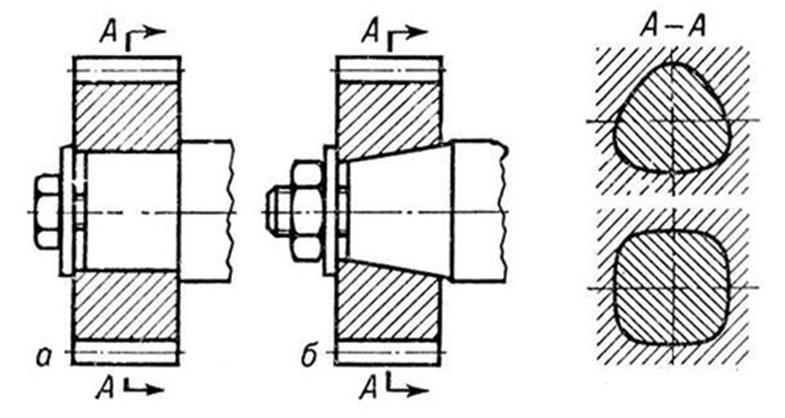

Достоинства профильных соединений: 1) отсутствие концентраторов напряжений кручения; 2) хорошее центрирование деталей соед; 3) повышенная надежность по критерию прочности соед по сравнению с соединениями с натягом.

профильных соединений: 1) сложность изготовления профпов; 2) при передаче соед-ямивращ М возникают знач распорные силы, деформирующие ступицы.

Виды прочностных расчетов

Различают проектировочные и проверочные расчёты.

Проектировочный расчёт выполняется, когда по ожидаемым нагрузкам, с учётом свойств материала определяются геометрические параметры деталей.

Проверочный расчёт выполняют, когда известна вся "геометрия" детали и максимальные нагрузки, а с учётом свойств материала определяются максимальные напряжения, которые должны быть меньше допускаемых.

Всегда, везде, при любых обстоятельствах конструктор обязан учитывать и обеспечивать такие условия работы, чтобы напряжения в материале деталей не превышали допускаемых.

В качестве допускаемых нельзя назначать предельные напряжения, при которых наступает разрушение материала.

Допускаемые напряжения следует принимать меньше предельных, "с запасом": [σ] = σпредельное/n,

где n - коэффициент запаса (обычно 1,2 < n < 2,5) .

В разных обстоятельствах коэффициент запаса может быть либо задан заказчиком, либо выбран из справочных нормативов, либо вычислен с учётом точности определения нагрузок, однородности материала и специфических требований к надёжности машин.

Выполнение всех видов прочностных расчётов для каждой детали займёт очень много времени. Поэтому инженер должен сначала изучить опыт эксплуатации подобных изделий. Это особенно удобно для типовых деталей и машин. Следует обратить внимание на то, какой вид поломок встречается чаще всего. Именно по этому виду поломок, точнее по вызывающим их напряжениям, следует выполнять предварительно проектировочный расчёт. По его результатам строится форма детали, а проверочный расчёт выполняется по напряжениям, вызывающим менее опасные дефекты.

В расчётах не следует гнаться за "абсолютной" точностью и использовать сложные "многоэтажные" формулы. Обширный опыт инженеров-расчётчиков показывает, что усложнение методик расчёта не даёт новых результатов.

Общие сведения о передачах.

Передача(в машинах) - устройство, предназначенное для передачи энергии на расстоянии и преобразования его параметров в скорость движения.

Необходимость обусловлена:

1) Несовпадение требований исполнения с оптимальн скоростью ДВС

2) регулируемость скорости

3) Преобразование видов движения

4) Распределение потоков мощности различными исполнительными органами

5) Реверсирование

Зубчатая передача-трёхзвенный механизм,кот образует между собой высшую пару.

Достоинства:

1)высокая надёжность работы в широком диапазоне скоростей и нагрузок

2)малые габариты, большоядолговечность,высокийкпд,постоянствопередатотнош

3)простота обслуживания

недостатки: повыш шум при больших скоростях

19/20Кручение прямого бруса круглого сечения. Построение эпюр крутящих моментов.

Кручением называют деформацию бруса, при которой в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент .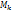

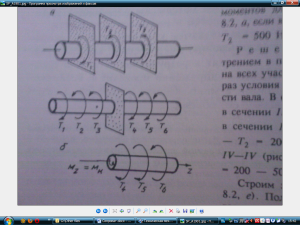Кручение имеет место при нагружении бруса моментами пар сил, расположенных в плоскостях, перпендикулярных к оси бруса (рис а). Внешние моменты пар сил, действующие на брус, являются вращающими моментами Т в отличие от крутящих моментов, возникающих в сечениях бруса. Работающие на кручение брусья называют валами.

Крутящие моменты определяют методом сечений. Вал рассекают плоскостью, перпендикулярной к ее продольной оси, мысленно отбрасывают одну часть вала, а действие отброшенной части на оставшуюся заменяют неизвестным моментом 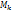(рис. б). Рассматривая условие равновесия 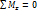, определяют значение .

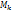Значение крутящего момента в сечении вала равно алгебраической сумме вращающихся (скручивающих) моментов, действующих с одной стороны от рассматриваемого сечения. Возможно любое правило знаков, но при решении конкретной задачи необходимо принимать один и тот же знак для вращающих моментов одного направления. Закон изменения крутящих моментов по длине бруса изображают в виде графика (эпюры). Эпюры – графики изменения внутренних силовых факторов. Они строятся для того. Чтобы установить наиболее нагруженные участки бруса и определить опасные сечения.

Шпоночные соединения

Шпо́ночноесоедине́ние — соединение охватывающей и охватываемой детали для передачи крутящего момента с помощью шпонки. Шпоночное соединение позволяет обеспечить подвижное соединение вдоль продольной оси. Классификация соединений в зависимости от формы шпонки: соединения призматическими шпонками, соединения клиновыми шпонками, соединения тангенциальными шпонками, соединения сегментными шпонками, соединения цилиндрическими шпонками. Шпонка представляет собой стальной брус, вставляе-мый в пазы вала и ступицы. Она служит для передачи момента между валом и ступицей колеса, шкива, звездочки. Основные типы шпонок стандартизированы.

Основной критерий работоспособности шпоночного соединения — прочность на смятие.

Достоинства шпоночных соединений:

• простота конструкции,

• легкость монтажа и демонтажа,

• низкая стоимость.

Недостатки шпоночных соединений:

• шпоночные пазы ослабляют прочность вала и ступицы,

• конструкция напряжений, возникающих в зоне шпоночного паза, снижает сопротивление усталости.

Шпоночные соединения подразделяются на:

• не напряженные: с использованием призматических и сегментных шпонок (при сборке в деталях не возни-кают предварительные напряжения);

• напряженные: с применением клиновых и тангенциальных шпонок (при сборке возникают монтажные на-пряжения).

Пара сил. Момент пары сил

Парой сил называется приложенная к твердому телу система двух сил (F,F') , равных по модулю, параллельных и направленных в противоположные стороны:F = -F'; F=F'.

Расстояние d между линиями действия сил пары называется плечом пары; плоскость , в которой действуют силы пары, называется плоскостью действия пары. Совокупность нескольких пар, действующих на тело, называется системой пар.

Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение. Вращательный эффект пары характеризуется векторной величиной, называемой моментом пары. Момент пары сил относительно точки O

MO(F,F') = MO(F) + MO(F') не зависит от выбора точки O и равен моменту одной из сил пары относительно точки приложения другой силы

M(F,F') = MA(F') = MB(F) .

Момент пары сил M перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары: M = F · d.

Векторный момент пары сил может быть приложен в любой точке пространства, т.е. является свободным вектором.

Две пары сил, имеющие одинаковые векторные моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие.

.Эквивалентность пар: действие пары сил на твердое тело не изменится, если

переместить пару в другое положение в плоскости ее действия;

плоскость ее действия переместить параллельно самой себе;

любым образом изменить модули сил и плечо пары, сохранив неизменным их произведение, т.е. момент пары M=F · d.

Сложение пар сил: система n пар сил с моментами M1,M2,...,Mn эквивалентна одной паре с моментом M, равным векторной сумме моментов этих пар: M = Mk.

Условие равновесия системы пар, приложенных к твердому телу: M = Mk=0.

Классификация подшипников

Подши́пник — изделие, являющееся частью опоры или упора, которое поддерживает вал, ось или иную подвижную конструкцию с заданной жёсткостью. Фиксирует положение в пространстве, обеспечивает вращение, качение или линейное перемещение с наименьшим сопротивлением, воспринимает и передаёт нагрузку от подвижного узла на другие части конструкции. По принципу работы все подшипники можно разделить на несколько типов: 1)подшипники качения; 2)подшипники скольжения; 3)газостатические подшипники; 3)газодинамические подшипники; 4)гидростатические подшипники; 5)гидродинамические подшипники; 6)магнитные подшипники. Основные типы, которые применяются в машиностроении — это подшипники качения и подшипники скольжения.

Подшипник представляет собой по существу планетарный механизм, в котором водилом является сепаратор, функции центральных колес выполняют внутреннее и наружное кольца, а тела качения заменяют сателлиты.Частота вращения сепаратора или частота вращения шариков вокруг оси подшипника: nc=n1/2(1-Dw/dm)

где n₁ — частота вращения внутреннего кольца радиального шарикоподшипника,
D_ω —диаметр шарика,
d_m = 0,5(D+d) — диаметр окружности осей шариков.

29.Момент силы относительно центра (или точки).Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее моментом

моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.Момент силы относительно центра О будем обозначать символом m0(F). Следовательно, 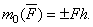Момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки, и знак минус, - если по ходу часовой стрелки. свойства момента силы:1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).3) Момент силы численно выражается удвоенной площадью треугольника 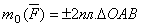Этот результат следует из того, что

Теория механизмов

Испытания проводят на гидровлических и механических разравных машинах. Они снабжаются диаграммным аппаратом который в процессе испытания вычёркивает зависимость между F, растягивающий образец и соответственно удлинением дельтаL

Диаграмма растяжения

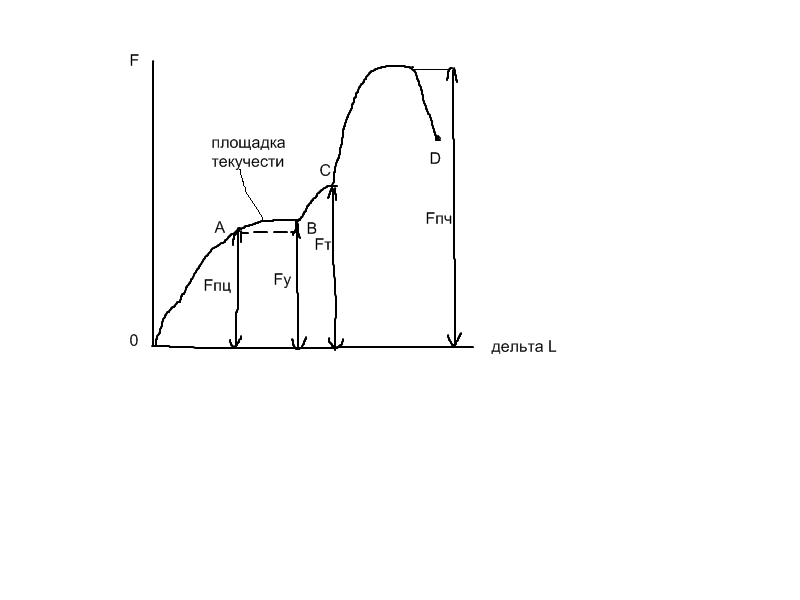
ОА-зона упругости

АВ-зона текучести

ВС-зона упрочнения

СВ-зона пластической деформации

Для того чтобы исключить влияния абсолютных размеров образца, Диаграмму перестраивают все ординаты делят на нач. площадь поперёк сечения, а все абсциссы на начально расчитаную длину.

Теория механизмов и машин 12

Формула Виллиса

, где 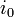— передаточное число при заблокированномводиле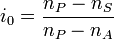

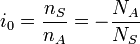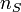, — скорость солнечной шестерни,

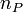- скорость водила и 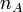— скорость кольцевой шестерни

Зубчатые механизмы с подвижными осями колес

К зубчатым механизмам с подвижными осями колес относятся дифференциальные и планетарные механизмы. Дифференциальным называется механизм, в котором оси некоторых колес имеют возможность перемещаться в пространстве. Колеса, оси которых не могут перемещаться, называются центральными, или солнечными, колесами дифференциальной передачи. Перемещающиеся колеса называются планетными колесами, или сателлитами. Звено, несущее подшипники подвижного колеса, называется водилом, или поводком. Дифференциальные механизмы практически используются для сложения нескольких движений или для разложения движения на слагаемые. Сложение нескольких движений в одно не­обходимо, например, в металлорежущих станках для получения независимых настроек при обработке отдельных участков детали (настройка на число зубьев и угол наклона зубьев нарезаемой косозубой шестерни), в универсальных делительных устройствах для облегчения настройки на заданное число делений и т. д. Разложение одного движения на слагаемые применяется, например, в приводе ведущих колес автомобиля для устранения проскальзывания их относительно дороги на поворотах. При определении чисел оборотов и передаточных чисел в дифференциальном механизме большое значение имеет направление вращения. Если ведущее и ведомое колеса при остановившемся поводке вращаются в одном направлении, то передаточное число считается положительным (+), если направление вращения их различно, то передаточное число считается отрицательным (-).

Гибкость стержней

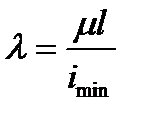- гибкость стержня. Она зависит от геометрических параметров сечения, условий закрепления стержня, его длины, вида нагружения. Если принять, что 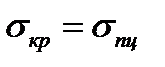, то можем найти предельную гибкость стержня 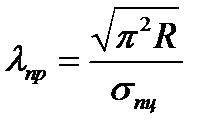. Т.о. применимость формулы Эйлера определяется условием 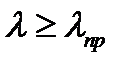, т.е. ее используют только тогда. Когда гибкость рассчитываемого стержня не меньше предельной. Если 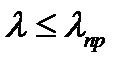, то критическое напряжение определяется по формуле Ясинского 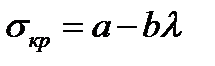, aи b– экспериментальные коэффициенты, зависят от свойств материала. В зависимости от гибкости стержни можно условно поделить на 3 группы: 1. Стержни большой гибкости 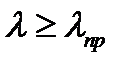; 2. Стержни средней гибкости 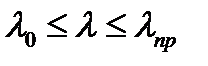; 3. Стержни малой гибкости (расчет на устойчивость не проводится).

Чистый сдвиг

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s₁= — s₃ = t; s₂= 0. Главные площадки составляют с площадками чистого сдвига угол 45^о.

При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,

g » — относительный сдвиг или угол сдвига.

Закон Гука при сдвиге: g = t/G или t = G×g .

G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).

Потенциальная энергия при сдвиге: .

Удельная потенциальная энергия деформации при сдвиге: ,

где V=а×F — объем элемента. Учитывая закон Гука, .

Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.

Передаточное отношение

Передаточное отношение( 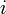) — одна из важных характеристик механической передачи вращательного движения, находится как отношение угловой скорости ведущего элемента ( 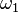) механической передачи к угловой скорости ведомого элемента( 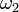) или отношение частоты вращения ведущего элемента ( 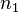) механической передачи к частоте вращения ведомого элемента ( 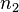) или отношение числа зубьев ( 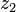) (длины окружности, радиуса, диаметра) ведомого элемента к числу зубьев ( 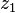) (длине окружности, радиусу, диаметру) ведущего элемента механической передачи.

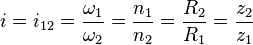
Характеристика передаточное отношение применима как к механической передаче с одной ступенью (одной кинематической парой), так и к механическим передачам со множеством ступеней. Во втором случае передаточное отношение всей механической передачи будет равно произведению передаточных отношений всех ступеней.^[1]

Механизмы с передаточным отношением больше единицы — редукторы (понижающие редукторы), меньше единицы — мультипликаторы (повышающие редукторы).

Величина, обратная передаточному отношению, называется передаточное число( ).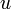

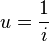
Тем не менее, в нынешнее время понятия передаточное отношение и передаточное число означают одно и то же. Например, ГОСТы 16532-70, 21354-87 и др. величину ( 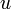) называют передаточным числом, а многие каталоги редукторов ту же величину называют передаточным отношением

.

Шлицевое (зубчатое) соединение — соединение вала (охватываемой поверхности) и отверстия (охватывающей поверхности) с помощьюшлицев (пазов) и зубьев (выступов), радиально расположенных на поверхности. Обладает большой прочностью, обеспечивает соосность вала и отверстия, с возможностью осевого перемещения детали вдоль оси.

По форме профиля шлицев (зубьев):Прямобочныеэвольвентныетреугольные.По передаваемой нагрузке:Легкая серия, Средняя серия, Тяжелая серия По способу центрированиясопрягаемых деталей:по наружному диаметру зубьев;по внутреннему диаметру зубьев;по боковым поверхностям зубьев.Поcтепениподвижности:подвижное;нормальное;неподвижное.

Аксиомы статики

Аксиома инерции. Под действием уравновешенной системы сил материальная точка (тело) находится в состоянии покоя или движется равномерно и прямолинейно.

Аксиома равновесия двух сил. Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

Аксиома присоединения и исключения уравновешивающихся сил. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать от него уравновешенную систему сил.

Аксиома параллелограмма сил. Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту точку и равную их геометрической сумме.

Аксиома равенства действия и противодействия. Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

Аксиома о сохранении равновесия сил, приложенных к деформируемому телу. Равновесие деформируемого тела не нарушится, если это тело отвердеет.

3.Кинематическая цепь - это система звеньев, образующих между собой кинематические пары. В зависимости от того, какие кинематические пары присутствуют в цепи и как они расположены, различают плоские и пространственные кинематические цепи. В плоской кинематической цепи все звенья движутся в одной или параллельных плоскостях (рис.1.2а.). Кинематическая цепь, звенья которой образуют замкнутый контур, называется замкнутой (рис.1.2б), если контур не замкнут, цепь называется незамкнутой или открытой (рис.1.2в). В традиционных механизмах обычно используются замкнутые кинематические цепи, незамкнутые цепи находят применение только в манипуляторах. Механизм – это кинематическая цепь, в которой указаны стойка, входные и выходные звенья.

На основе кинематических цепей можно получать не только механизмы, но и устройства, заменяющие некоторые кинематические пары, так называемые кинематические соединения (рис.1.3). Шарико- или роликоподшипник эквивалентен вращательной паре. Роликовые направляющие заменяют поступательную пару. Винтовая пара качения заменяет обычную винтовую пару. Карданный шарнир, он же называется шарниром Гука или универсальным шарниром, заменяет сферическую пару с пальцем. Если вилку снабдить еще одной вращательной парой получим аналог сферической пары. Крестовое соединение допускает два поступательных движения без вращения.

Напряжение как мера внутренних сил.

Величину интенсивности внутренних сил в точке поперечного сечения называют механическимнапряжением. Напряжение характеризует величину внутренней силы, приходящейся на единицу площади поперечного сечения.

Рассмотрим брус, к которому приложена внешняя нагрузка (рис.1).с помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие оставшейся правой части. Выделим на секущей плоскости малую площадку ∆А. На этой площадке действует равнодействующая внутренних сил упругости. Направление напряжения 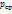совпадает с направлением внутренней силы в этом сечении.

Вектор называют полнымнапряжением. Его принято раскладывать на два вектора (рис.2):

τ - лежащий в площадке сечения (касательноенапряжение)

σ – направленный перпендикулярно площадке (нормальноенапряжение).

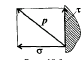
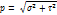
Если p – пространственный, то его раскладывают на три составляющие:

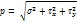
Нормальноенапряжение характеризует сопротивление сечения растяжению или сжатию. Касательноенапряжение характеризует сопротивление сечения сдвигу. Сила N (продольная) вызывает появление нормального напряжения σ. Силы 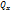и 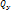вызывают появление касательных напряжений τ. Моменты изгибающие 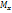и 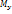вызывают появление нормальных напряжений σ, переменных по сечению. Крутящий момент 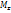вызывает сдвиг сечения вокруг продольной оси, поэтому появляются касательные напряжения τ.