Интегралы от некоторых рациональных функций
Обозначение: 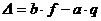 .
.
1. 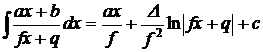 . 2. . 2. 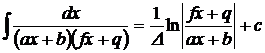 , , 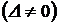 . 3. . 3. 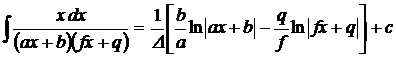 , , 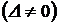 . 4. . 4. 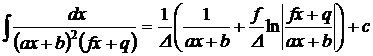 , , 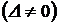 . 5. . 5. 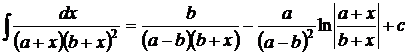 , , 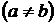 . 6. . 6. 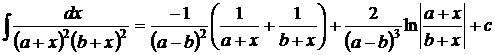 , , 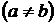 . 7. . 7. 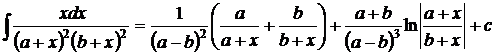 , , 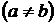 . 8. . 8. 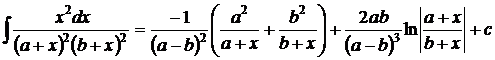 , , 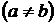 . 9. . 9. 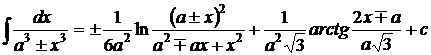 . 10. . 10. 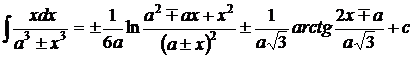 . 11. . 11. 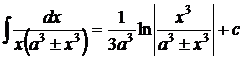 . 12. . 12. 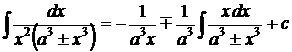 . 13. . 13. 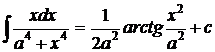 . 14. . 14. 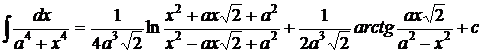 . 15. . 15. 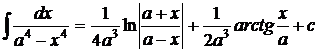 . 16. . 16. 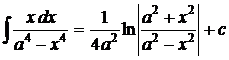 . 17. . 17. 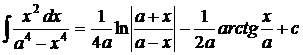 . . |
6. Интегралы, содержащие тригонометрические и показательные
функции
1. 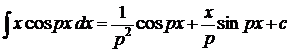 . 2. . 2. 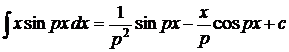 . 3. . 3. 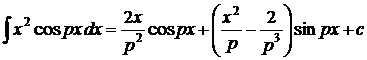 . 4. . 4. 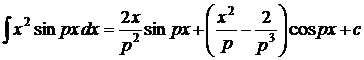 . 5. . 5. 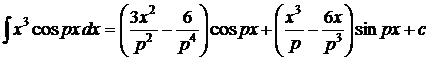 . 6. . 6. 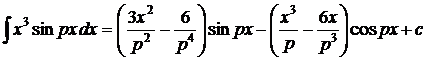 . 7. . 7. 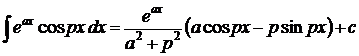 8. 8. 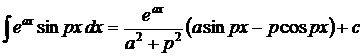 . 9. . 9. 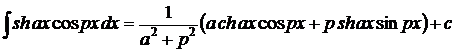 . 10. . 10. 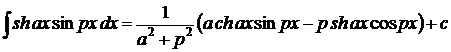 . 11. . 11. 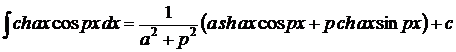 . 12. . 12. 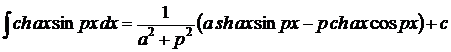 . 13. . 13. 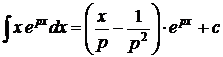 . 14. . 14. 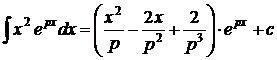 . . |
Несобственные интегралы
| Условие | Определение и обозначение | Геометрическая иллюстрация сходящихся интегралов | |
| 1. Интегралы с бесконечными пределами интегрирования | 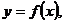 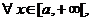 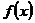 - непрерывна на - непрерывна на 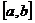 , где , где 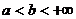 | 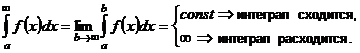 |  |
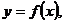 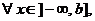 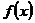 - непрерывна на - непрерывна на 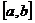 , где , где 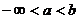 | 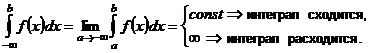 | 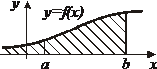 | |
   - непрерывна на - непрерывна на 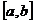 , где , где 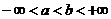 |  интеграл сходится, если сходятся оба интеграла интеграл сходится, если сходятся оба интеграла 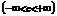 |  | |
| 2. Интегралы от неограниченных функций | 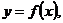 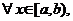 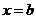 - точка бесконечного разрыва - точка бесконечного разрыва | 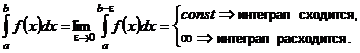 | 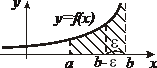 |
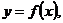 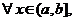 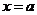 - точка бесконечного разрыва - точка бесконечного разрыва | 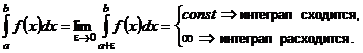 | 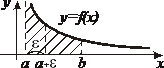 | |
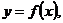 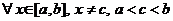 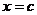 - точка бесконечного разрыва - точка бесконечного разрыва | 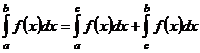 интеграл сходится, если сходятся оба интеграла сходятся интеграл сходится, если сходятся оба интеграла сходятся | 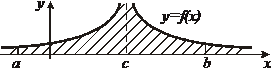 | |
| Замечание 1. Если при отыскании предела окажется, что он не существует, то несобственный интеграл типа 1 и 2 называется расходящихся | |||
| 3. Теоремы сравнения | 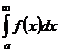 - сходится, - сходится, 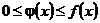 , , 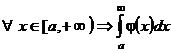 - сходится, - сходится, 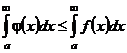 | ||
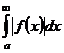 - сходится Þ - сходится Þ 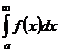 - сходится абсолютно - сходится абсолютно | |||
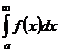 - расходится, - расходится, 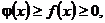 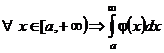 - расходится - расходится | |||
| Замечание 2. Теоремы сравнения имеют место и для всех интегралов типа 1 и 2 |
Функции нескольких переменных
| Определение функции | Графическое изображение | Множество равных уровней | Предел функции | Непрерывность | |||
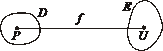 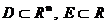 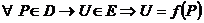 (функция (функция 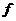 отображает множество отображает множество  на множество на множество 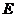 ) В частности, 1. ) В частности, 1. 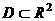 , , 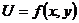 . 2. . 2. 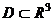 , , 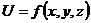 . . |   , ,  . .  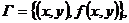 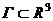 - график функции - график функции 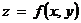 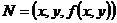 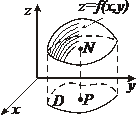 | 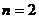 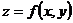 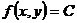 , где , где 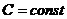 - линия уровня - линия уровня    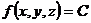 , где , где 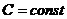 - поверхность уровня - поверхность уровня | 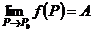 , если 1. , если 1. 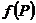 определена в некоторой окрестности определена в некоторой окрестности 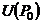 точки точки 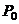 ; 2. ; 2. 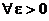 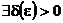 : : 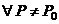 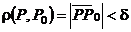 выполняется выполняется 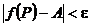 . Замечание. Предел функции не зависит от способа стремления т. . Замечание. Предел функции не зависит от способа стремления т. 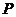 к т. к т. 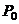 | Функция 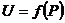 называется непрерывной в точке называется непрерывной в точке 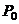 , если: 1. , если: 1. 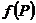 определена в точке определена в точке 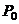 и некоторой ее окрестности и некоторой ее окрестности 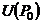 ; 2. ; 2. 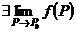 ; 3. ; 3. 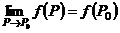 или или  где где 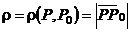 | |||
| Частные производные | Дифференциал | ||||||
| Определение | Геометрическое изображение | Определение | Применение дифференциала к приближенным вычислениям | ||||
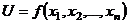 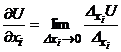 , , 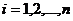 В частности, В частности, 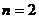 , , 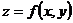 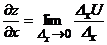 ; ; 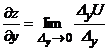 Замечание. Частная производная по переменной Замечание. Частная производная по переменной 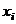 находится по правилам дифференцирования функции одной переменной, причем, остальные переменные рассматриваются как постоянные. находится по правилам дифференцирования функции одной переменной, причем, остальные переменные рассматриваются как постоянные. | 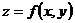 , , 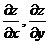 , т. , т. 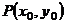 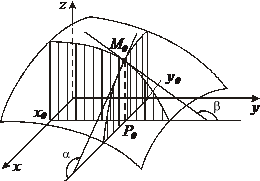 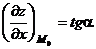 ; ; 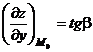 | 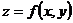 - дифференцируемая функция в т. - дифференцируемая функция в т. 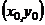 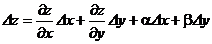 , где , где 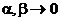 при при 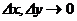 . . 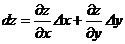 - главная часть приращения – дифференциал - главная часть приращения – дифференциал 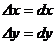 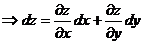 | 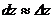 , , 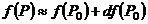 , В частности, , В частности, 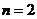 , , 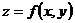 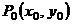 , , 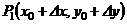 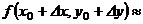 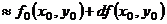 , где , где 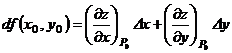 | ||||
9. Дифференциальное исчисление функций нескольких переменных (n=2)
| Сложные функции и их дифференцирование | Неявно заданные функции и их дифференцирование | |||
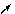 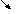 1. 1. 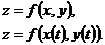 , где , где 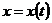 , , 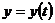 . . 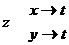 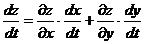 - полная производная - полная производная  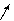 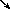 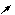 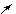 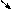 2. 2. 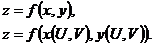 , где , где 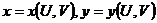 , , 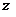 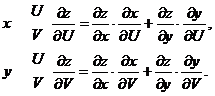 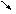  3. 3. 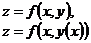 где где 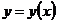 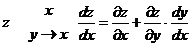 - полная производная - полная производная | Уравнение 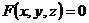 определяет неявное задание функции определяет неявное задание функции 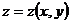 переменных переменных 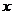 и и 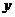 . . 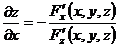 , , 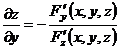 , где , где 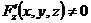 | |||
| Приложения дифференциального исчисления | ||||
| Экстремум функции 2-х переменных | Касательная плоскость и нормаль к поверхности | |||
| Определение | Необходимые условия существования экстремума | Достаточные условия существования экстремума | 1) 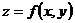 - уравнение поверхности - уравнение поверхности 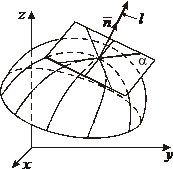 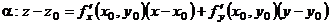 - уравнение касательной плоскости - уравнение касательной плоскости 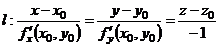 - - 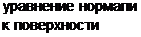 2) 2) 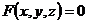 - уравнение поверхности. - уравнение поверхности. 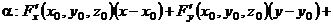 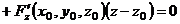 - уравнение кас. плоскости - уравнение кас. плоскости 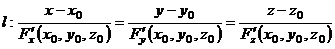 - уравнение нормали к поверхности - уравнение нормали к поверхности | |
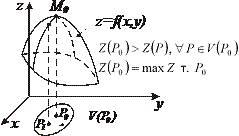 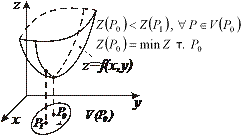 | 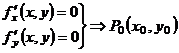 - стационарная точка функции - стационарная точка функции 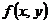 . Замечание. Экстремум возможен и в тех точках, где хотя бы одна из частных производных не существует . Замечание. Экстремум возможен и в тех точках, где хотя бы одна из частных производных не существует | 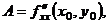 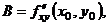 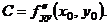 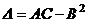 . 1. . 1. 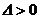 а) а) 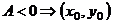 - т. - т.  б) б) 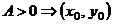 - т. - т. 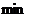 2. 2. 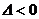 - в точке - в точке 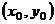 нет экстремума 3. нет экстремума 3. 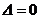 - требуются дополнительные условия - требуются дополнительные условия | ||
Задачи о массе фигуры
| Фигура Ф | Прямой стержень   | Изогнутый стержень   | Плоская пластина  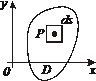 | Изогнутая пластина 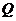  | Тело  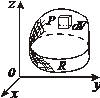 |
Плотность 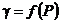 | 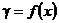 | 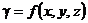 | 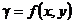 | 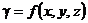 | 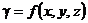 |
Элемент меры 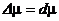 | 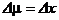 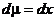 | 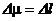 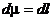 | 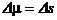 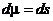 | 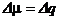 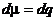 | 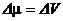 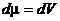 |
Элемент массы 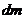 | 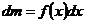 | 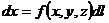 | 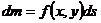 | 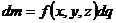 | 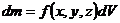 |
Масса 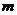 фигуры фигуры | 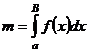 | 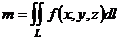 | 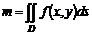 | 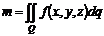 |  |
