Некоторые интегралы, содержащие квадратный трехчлен.
Учебные карты. Часть 2
Интегральное исчисление. Функции многих переменных.
Кратные интегралы. Элементы теории поля.
Дифференциальные уравнения. Ряды.
Магнитогорск 2006
Составитель: ст. препод. Н.И. Кимайкина
Учебные карты. Часть 2. Интегральное исчисление. Функции многих переменных. Кратные интегралы. Элементы теории поля. Дифференциальные уравнения. Ряды.
Магнитогорск: МГТУ, 2006.
В настоящем издании дан комплект учебных карт к главам программы по курсу «Высшая математика», которые изучаются во втором семестре. Учебные карты содержат весь существенный материал, составляющий ядро курса. Во введении изложена методика проведения практических занятий, когда в основу его положено введение структурной схемы алгоритмического построения изучаемого материала. Результатом занятия является учебная карта или страница по изучаемой теме.
Рецензент: Гугина Е.М., старший преподаватель каф. математики
Оглавление
Введение. 3
1. Таблица производных. 4
2. Таблица интегралов. 5
3. Методы интегрирования. 6
4. Некоторые интегралы, содержащие квадратный трехчлен. 7
5. Интегралы от некоторых рациональных функций.. 8
6. Интегралы, содержащие тригонометрические и показательные функции.. 9
7. Несобственные интегралы.. 10
8. Функции нескольких переменных. 11
9. Дифференциальное исчисление функций нескольких переменных (n=2) 12
10. Задачи о массе фигуры.. 13
11.Криволинейный интеграл по длине дуги.. 13
12. Системы координат. 14
13. Двойной интеграл. 15
14. Тройной интеграл. 15
15. Приложения интегралов по фигуре в геометрии.. 16
16. Приложение интегралов по фигуре в механике. 18
17. Скалярное поле (стационарное) 19
18. Векторное поле. Характеристики векторного поля. 20
19. Дифференциальные уравнения первого порядка. 22
20. Виды дифференциальных уравнений высших порядков, допускающих понижение порядка 23
21. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами.. 23
22. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами.. 24
23. Числовые ряды. Основные понятия. 25
24. Числовые ряды с положительными членами.. 26
25. Знакопеременные числовые ряды.. 27
26. Функциональные ряды. Основные понятия. 28
27. Степенные ряды.. 29
28. Разложение функции в степенной ряд. 29
29 .Таблица разложений некоторых функций в степенные ряды.. 30
30. Разложение функции в тригонометрический ряд Фурье. 31
Введение
В курсе математики практическим занятиям отводится почти половина учебного времени, где студент должен: а) овладеть системой основных понятий; б) обучиться стандартному применению алгоритмов и способов решений различных классов задач; в) овладеть умением обобщать и творчески подходить к решению задач.
Упражнения обеспечивают усвоение, углубление и закрепление учебного материала, формируют умение и навыки. На упражнениях развивается одно из основных умений работать самостоятельно – умение выделять главное в изучаемом материале.
Учебные карты есть результат многолетней работы преподавателей кафедры высшей математики. Для обучения выделению главного в изучаемом материале предусматривается новая методика проведения практических занятий, которая рассчитана на самостоятельное изучение теоретического материала и составление студентами учебной карты или справочной страницы по изучаемой теме, облегчающей решение типовых задач и усвоение теоретического материала. Процесс обучения как бы делится на три этапа.
1 этап. Кроме выдачи обычного домашнего задания по закреплению пройденного материала, преподаватель указывает тему следующего занятия и выдает студентам вопросы, по которым они первично обрабатывают теоретический материал. Эти вопросы ориентируют студентов на отбор основных теоретических понятий, выделению типовых задач, выработку способов их решений. Результатом этого этапа является черновик так называемой учебной карты.
2 этап. На занятии содержание учебной карты обсуждается, уточняется. Окончательно выработанным вариантом студент пользуется в процессе занятия. Появляется возможность составить более краткую справочную страницу по изучаемой теме.
3 этап. Работая дома по закреплению материала, окончательный вариант учебной карты студент заносит в специальную тетрадь и впоследствии по мере надобности пользуется ею.
Комплект учебных карт создается по всему курсу. В сжатой символической форме с необходимыми геометрическими иллюстрациями в них отражен математический аппарат, необходимый для решения задач. Учебная карта – алгоритмическая схема построения изучаемой темы – не обязательно должна иметь застывшую форму. Она - плод совместной работы студентов с преподавателем.
Комплект учебных карт издан к главам программы курса «Высшая математика», включающим материал второго семестра, и может быть рекомендован как наглядное пособие на 2-м этапе занятия и как методическое пособие по организации самостоятельной работы студентов для преподавателей.
Таблица производных
| Элементарные функции | Сложные функции | |
| Степенные функции | 1.  а. а.  b. b.  c. c.  d. d.  |    |
| Показательные функции | 2.  а. а.  |   |
| Тригонометрические функции | 3.  4. 4.  5. 5.  6. 6.  |     |
| Логарифмические функции | 7.  a. a.  |  |
| Обратные тригонометрические функции | 8.  9. 9.  10. 10.  11. 11.  |   |
| Гиперболические функции | 12.  13. 13.  14. 14.  15. 15.  | |
| Правила дифференцирования |      ; ;  |
Таблица интегралов
| Элементарные функции | Сложные функции | |
| Степенные функции | 1.  , ,  а. а.  , b. , b.  , c. , c.  . . | 1.   b. b.  d. d.  |
| Показательные функции | 2.  , a. , a.  . . | 2.  a. a.  |
| Тригонометрические функции | 3.  4. 4.  5. 5.  6. 6.  | 3.  4. 4.  5. 5.  6. 6.  |
| Логарифмические функции | 7.  | 7a.  |
| Обратные тригонометрические функции | 8.  9. 9.  10. 10.  11. 11.  | 8.  10. 10.  |
| Гиперболические функции | 12.  13. 13.  14. 14.  15. 15.  | 18.  19. 19.  20. 20.  21. 21.  |
| Правила дифференцирования | 16.  17. 17.  | |
 , где , где  |
Методы интегрирования
| 1. Непосредственное интегрирование | 2. Замена переменной (подстановка) | 3. Интегрирование по частям | ||
Выполняется: 1. По таблице интегралов и свойствам: а)  б) б)  в) в)  2. С использованием преобразований: а) почленное деление; б) выделение целой части; в) применение тригонометрических тождеств г) выделение полного квадрата 2. С использованием преобразований: а) почленное деление; б) выделение целой части; в) применение тригонометрических тождеств г) выделение полного квадрата | Применяется: 1. При интегрировании некоторых классов функций:  . 2. При наличии дифференциальной связи: . 2. При наличии дифференциальной связи:  (за новую переменную принимают функцию, от которой в подынтегральном выражении есть дифференциал) (за новую переменную принимают функцию, от которой в подынтегральном выражении есть дифференциал) |  1. 1.   2. 2.   | ||
| 4. Стандартные приемы и подстановки при интегрировании некоторых классов функций | ||||
| а) рациональные дроби | б) тригонометрические выражения | в) иррациональные выражения | ||
1. Простейшие дроби I.  . II. . II.  . III. . III.  . IV. . IV.  , ,  . Алгоритм преобразования дробей вида III и IV: 1) Выделить полный квадрат: . Алгоритм преобразования дробей вида III и IV: 1) Выделить полный квадрат:  2) Применить подстановку: 2) Применить подстановку:  3) Разложить на два интеграла вида: 7а, 11 (табличные). 4) Для дроби вида IV применить формулу: 3) Разложить на два интеграла вида: 7а, 11 (табличные). 4) Для дроби вида IV применить формулу:  . 2. Рациональные дроби вида . 2. Рациональные дроби вида  Алгоритм интегрирования: 1. Если дробь неправильная Алгоритм интегрирования: 1. Если дробь неправильная  , то выделить целую часть. 2. Разложить знаменатель , то выделить целую часть. 2. Разложить знаменатель  на простые множители: на простые множители:  . 3. Правильную дробь разложить на сумму простейших дробей . 3. Правильную дробь разложить на сумму простейших дробей  (*) 4. Привести правую часть равенства (*) к общему знаменателю и уравнять числители левой и полученной правой частей 5. Найти коэффициенты (*) 4. Привести правую часть равенства (*) к общему знаменателю и уравнять числители левой и полученной правой частей 5. Найти коэффициенты  , применив к целому выражению: а) метод частных значений , применив к целому выражению: а) метод частных значений  ; б) метод сравнения коэффициентов при одинаковых степенях; 6. Проинтегрировать простейшие дроби. ; б) метод сравнения коэффициентов при одинаковых степенях; 6. Проинтегрировать простейшие дроби. | Универсальная подстановка 1.  Частные случаи: 1.1. Частные случаи: 1.1.   - нечетная относительно « - нечетная относительно «  » 1.2. » 1.2.   - нечетная относительно « - нечетная относительно «  » 1.3. » 1.3.   - четная в совокупности. 2. - четная в совокупности. 2.  , где , где  и и  четные, четные,  Применить формулы понижения: Применить формулы понижения:    3. 3.    4. 4.  , ,  Применяется: Применяется:  , ,  | 1. Линейная иррациональность   , где , где  - наименьший общий знаменатель - наименьший общий знаменатель  2. Квадратичные иррациональности. 2.1. 2. Квадратичные иррациональности. 2.1.  2.2. 2.2.  2.3. 2.3.  3. 3.  Смотри алгоритм интегрирования дроби вида III. Сводится к интегралам 1, 9, 18 таблицы №2 4. Смотри алгоритм интегрирования дроби вида III. Сводится к интегралам 1, 9, 18 таблицы №2 4.  , ,  - обратная подстановка. - обратная подстановка. | ||
Несобственные интегралы
| Условие | Определение и обозначение | Геометрическая иллюстрация сходящихся интегралов | |
| 1. Интегралы с бесконечными пределами интегрирования | 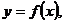 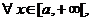 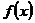 - непрерывна на - непрерывна на 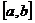 , где , где 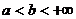 | 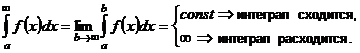 | 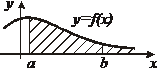 |
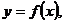 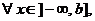 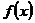 - непрерывна на - непрерывна на 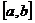 , где , где 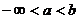 | 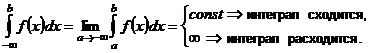 | 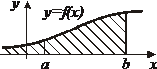 | |
  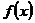 - непрерывна на - непрерывна на 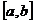 , где , где 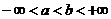 |  интеграл сходится, если сходятся оба интеграла интеграл сходится, если сходятся оба интеграла 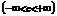 |  | |
| 2. Интегралы от неограниченных функций | 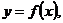 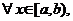 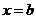 - точка бесконечного разрыва - точка бесконечного разрыва | 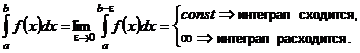 | 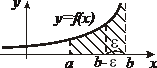 |
   - точка бесконечного разрыва - точка бесконечного разрыва | 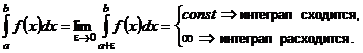 | 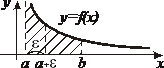 | |
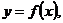 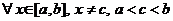 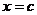 - точка бесконечного разрыва - точка бесконечного разрыва | 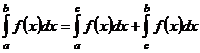 интеграл сходится, если сходятся оба интеграла сходятся интеграл сходится, если сходятся оба интеграла сходятся | 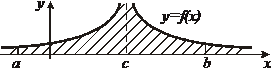 | |
| Замечание 1. Если при отыскании предела окажется, что он не существует, то несобственный интеграл типа 1 и 2 называется расходящихся | |||
| 3. Теоремы сравнения | 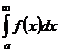 - сходится, - сходится, 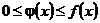 , , 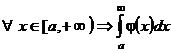 - сходится, - сходится, 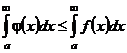 | ||
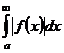 - сходится Þ - сходится Þ 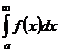 - сходится абсолютно - сходится абсолютно | |||
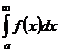 - расходится, - расходится, 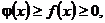 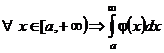 - расходится - расходится | |||
| Замечание 2. Теоремы сравнения имеют место и для всех интегралов типа 1 и 2 |
Задачи о массе фигуры
| Фигура Ф | Прямой стержень 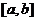 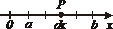 | Изогнутый стержень 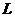 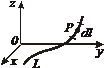 | Плоская пластина  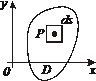 | Изогнутая пластина  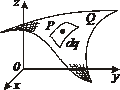 | Тело  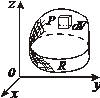 |
Плотность 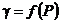 | 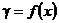 | 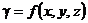 | 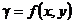 | 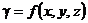 | 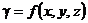 |
Элемент меры 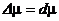 | 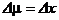 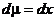 | 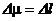 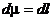 | 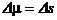 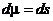 | 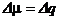 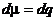 | 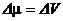 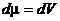 |
Элемент массы 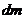 | 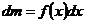 | 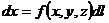 | 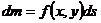 | 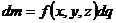 | 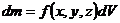 |
Масса 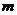 фигуры фигуры | 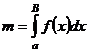 | 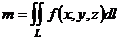 | 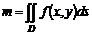 | 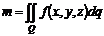 |  |
Системы координат
| Декартовы координаты | Полярные координаты и их связь с декартовыми | Цилиндрические координаты | Сферические координаты и их связь с декартовыми |
  ; ;    - радиус - вектор точки - радиус - вектор точки    , ,    ; ;  ; ;   |   ; ;   ; ;   |     ; ;    ; ;  |   ; ;   ; ;    ; ;      |
       |
Двойной интеграл
Геометрический смысл     |  |  , ,  |   |
 |  , ,  |   | |
 |  , ,  |   |
Тройной интеграл
Поверхностный интеграл I рода   |   |  | |
 где где  |  где где  |  где где  |    |
   |   |   |    |
Приложение интегралов по фигуре в механике
| фигура наи- мено- вание ве-личины |  |  |  |  |  |
1. Масса физической фигуры   плотность плотность |  |  |  |  |  |
2. Мера фигуры  |  |  |  |  |  |
3. Статический момент   |   |    |   |    |    |
4. Координаты центра тяжести (масс для однородного тела)  |   |    |   |    |    |
5. Момент инерции   |    |         |    |         |         |
Числовые ряды. Основные понятия
| № п/п | Понятие | Определение и обозначение | ||
| 1. | Ряд | 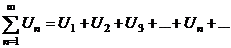 | ||
| 2. | Члены ряда, общий ( n – ый ) член ряда | 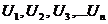 - бесконечная числовая последовательность, где - бесконечная числовая последовательность, где 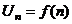 | ||
| 3. | Частичные суммы ряда | 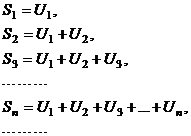 | ||
| 4. | Последовательность частичных сумм | 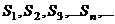 | ||
| 5. | Сходящиеся ряды | 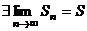 , где , где 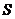 – сумма ряда – сумма ряда 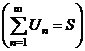 | ||
| 6. | Расходящиеся ряды | 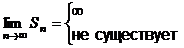 | ||
| 7. | Остаток ряда | 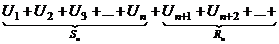 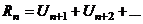 | ||
| Основные свойства сходящихся рядов | ||||
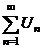 сходится сходится | 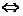 | 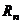 - сходится - сходится | ||
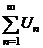 сходится, сходится, 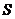 – его сумма – его сумма |  | 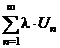 сходится, сходится, 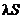 - его сумма - его сумма | ||
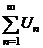 сходится, сходится, 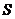 – его сумма – его сумма |  | 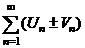 - сходится и - сходится и | ||
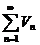 сходится, сходится, 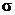 – его сумма – его сумма | 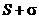 - его сумма - его сумма | |||
| Необходимый признак сходимости ряда | ||||
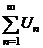 - сходится - сходится |  | 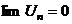 | ||
Следствие: 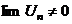 |  | 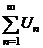 - расходится - расходится | ||
Функциональные ряды. Основные понятия
| Понятие | Определение и обозначение | ||
| 1. Функциональный ряд | 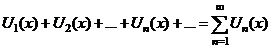 | ||
| 2. Члены ряда | 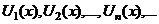 - функции от - функции от 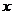 | ||
3. Сходимость ряда в точке 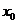 | 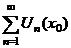 сходится сходится  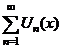 сходится в т. сходится в т. 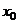 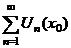 расходится расходится  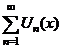 расходится в т. расходится в т. 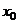 | ||
| 4. Область сходимости ряда | 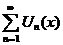 сходится сходится 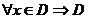 - область сходимости; - область сходимости;  - находится: - находится: 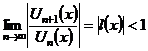 или или 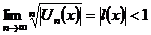 , , | ||
| 5. Последовательность частичных сумм | 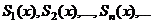 , где , где 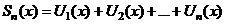 , , 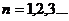 | ||
| 6. Сумма сходящегося ряда | 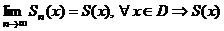 - сумма ряда - сумма ряда | ||
| 7. Остаток ряда | 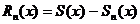 | ||
8. Равномерная сходимость ряда 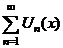 на на  | 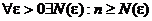 и и 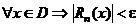 | ||
| 9. Абсолютная и равномерная сходимость ряда (признак Вейерштрасса) | 1. 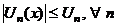 и и 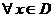 2. числовой ряд 2. числовой ряд 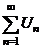 - сходится - сходится | Þ | 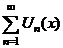 - сходится абсолютно и равномерно на - сходится абсолютно и равномерно на  |
| Свойства равномерно сходящихся рядов | |||
1. 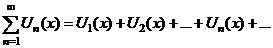 - равномерно сходится на - равномерно сходится на  2. 2. 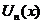 - непрерывна - непрерывна 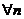 и и 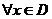 3. 3. 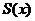 - его сумма - его сумма 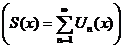 | Þ | 1. 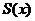 - непрерывна на - непрерывна на  2. 2. 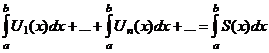 , где , где 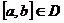 (почленное интегрирование) 3. (почленное интегрирование) 3. 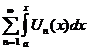 - равномерно сходится на - равномерно сходится на  , где , где
|
