Разностное уравнение и дискретная цепь
Непрерывный сигнал на входе линейной системы x(t) и соответствующий сигнал y(t) на выходе связаны дифференциальным уравнением. Замена непрерывной переменной t на дискретную переменную nT приводит к замене дифференциального уравнения разностным уравнением. Каноническая форма разностного уравнения общего вида, учитывающая в явном виде наличие в системе как прямых, так и обратных связей, запишется так
y(nT) = 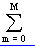 am x(nT - mT) +
am x(nT - mT) + 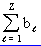 y(nT -
y(nT -  ), (2.1)
), (2.1)
где (M + 1) - число прямых связей,
Z - число обратных связей,
m, 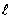 , n - целые положительные числа.
, n - целые положительные числа.
Аналитические методы решения разностных уравнений во многом повторяют методы решения дифференциальных уравнений и позволяют получить решение в общем виде, пригодном для анализа работы дискретной системы. Численные методы решения приводят к результату в виде числовой последовательности, поэтому разностное уравнение в этом случае воспринимается как алгоритм функционирования дискретной системы, пригодной для программирования на ЭВМ работы такой системы.
Система работа которой описывается разностными уравнениями, является дискретной так как она способна воздействовать только на отсчеты сигнала. Дискретная система и дискретная цепь осуществляет, согласно (2.1) следующие операции над дискретными сигналами.
Сдвиг (запаздывание) на целое число интервалов T
Умножение на некоторый коэффициент am или b 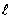
Z преобразование
Определение z-преобразования. Z- преобразование является обобщением дискретного преобразования Фурье. Особенно эффективно оно используется при анализе дискретных систем и, в частности, при проектировании рекурсивных цифровых фильтров.
Впервые z-преобразование введено в употребление П.Лапласом в 1779 и повторно "открыто" В.Гуревичем в 1947 году с изменением символики на z-k. В настоящее время в технической литературе имеют место оба вида символики. На практическое использование преобразования это не влияет, т.к. смена знака только зеркально изменяет нумерацию членов полинома (относительно z0), числовое пространство которых в общем случае от -¥ до +¥. В дальнейшем в качестве основной будем использовать символику положительных степеней z, давая пояснения по особенностям отрицательной символики, если таковая имеется.
Свойства z-преобразования
Рассмотрим некоторые свойства z-преобразования.
Свойство 1. Линейность. Z-образ суммы двух сигналов равен сумме z-образов этих сигналов. Действительно, пусть есть два дискретных сигнала 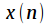 и
и 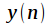 ,
, 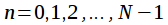 . Найдем z-преобразование их суммы
. Найдем z-преобразование их суммы 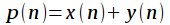 :
:
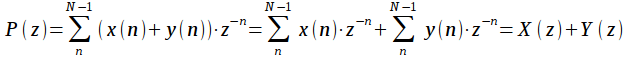 | (11) |
Свойство 2. Свойство задержки. Пусть дан исходный дискретный сигнал 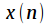 ,
, 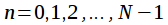 . Найдем z-преобразование сигнала
. Найдем z-преобразование сигнала 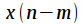 , задержанного на
, задержанного на 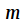 отсчетов:
отсчетов:
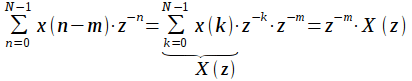 | (12) |
При выводе была введена переменная 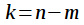 , тогда
, тогда 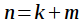 и получили, что задержка исходного сигнала на
и получили, что задержка исходного сигнала на 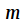 добавляет множитель
добавляет множитель 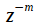 к z-преобразованию сигнала. Тогда задержка на один отсчет соответствует
к z-преобразованию сигнала. Тогда задержка на один отсчет соответствует 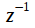 .
.
Свойство 3. Теорема о свертке. Пусть дано два сигнала 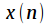 и
и 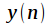 ,
, 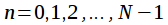 . Найдем z-преобразование их круговой свертки.
. Найдем z-преобразование их круговой свертки.
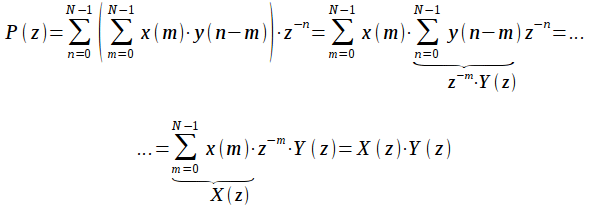 | (13) |
При выводе было использовано свойство задержки z-преобразования. Таким образом z-преобразование свертки сигналов равно произведению их z-образов.
