Полунепрерывный канал (дискретный канал непрерывного времени).

Каналы

Непрерывный канал. Это канал связи предназначенный для передачи непрерывных (аналоговых) сигналов. Например, абонентская телефонная линия, канал ТЧ.

Дискретный канал. Совместно с каналом связи УПС образуют дискретный канал, то есть канал, предназначенный для передачи только дискретных сигналов (цифровых сигналов данных).

Различают синхронные и асинхронные дискретные каналы.

В синхронных дискретных каналах ввод каждого единичного элемента производится в строго определенные моменты времени и они предназначены для передачи только изохронных сигналов.

По асинхронному каналу можно передавать любые сигналы - изохронные, анизохронные.

Расширенный канал. Дискретный канал в совокупности с кодером и декодером канала (УЗО) называется расширенным дискретным каналом (РДК).

В технике передачи данных РДК называют каналом передачи данных.

Передаточная функция дискретной цепи.

Замена сигналов в разностном уравнении (2.1) на Z - изображения этих сигналов

,

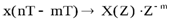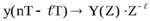
приводит к алгебраизации разностного уравнения

.

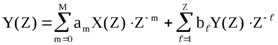Алгебраизация осуществляется применением теорем линейности и запаздывания.

Переход в область Z - изображений позволяет ввести понятие передаточной функции дискретной цепи H(Z), которая определяется как отношение Z - изображения сигнала на выходе цепи к Z - изображению сигнала на входе цепи. Поэтому, учитывая алгебраическую форму разностного уравнения общего вида, можно записать общий вид передаточной функции дискретной цепи

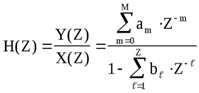. (2.3)

Отсюда, в частности, для нерекурсивной цепи

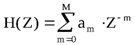. (2.4)

Если нерекурсивная цепь состоит всего из одного элемента запаздывания, то ,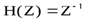

что находит своё отражение в обозначении элементов памяти на схемах дискретных цепей.

Передаточная функция конкретной цепи формируется по передаточным функциям её элементов согласно общих правил линейных цепей. В частности, для цепи содержащей ОС применяется известная формула

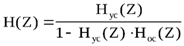, (2.5)

где 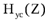- передаточная функция цепи прямого прохождения сигнала, 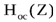- предаточная функция цепи ОС.

Цифровые фильтры

Устройства, осуществляющие линейную фильтрацию сигналов цифро­выми методами (т. е. с использованием средств цифровой вычислитель­ной техники), получили название цифровых фильтров.

Если определена функция передачи F(z) цифрового фильтра, свой­ства которого повторяют свойства аналогового фильтра-прототипа с функцией передачи F(p), то по ней просто строится каноническая схема, которую можно рассматривать как алгоритм обработки сигнала. Цифровую фильтрацию сигналов осуществляют на основе выполнения операций только трех типов: задержки, сложения и умножения. По­этому алгоритм цифровой обработки может быть реализован двумя способами: универсальной ЭВМ, выполняющей цифровую обработку по специальной программе, или специализированным вычислительным устройством, выполняющим только три указанные выше операции. Первый способ реализации алгоритма цифровой фильтрации называют программным, второй — аппаратурным.

Программный способ реализации эффективен при модели­ровании различных систем цифровой обработки сигналов, так как поз­воляет легко изменять алгоритм фильтрации. Цифровые фильтры, предназначенные для работы в системах автоматики, телемеханики и связи, должны обрабатывать сигналы в реальном масштабе времени, т. е. за время, не большее периода дискретизации входных сигналов, что является их особенностью. Использование универсальных ЭВМ для этих целей практически невозможно из-за их сравнительно низ­кого быстродействия и значительной стоимости. Аппаратур­ная реализация цифровых фильтров основана на использовании циф­ровых интегральных схем, представляющих собой регистры сдвига, сумматоры, умножители и т. п. Она стала возможной в связи с появле­нием в последние годы больших интегральных схем, имеющих большие функциональные возможности и высокое быстродействие.

По сравнению с аналоговыми цифровые фильтры имеют ряд досто­инств, к которым относят высокую стабильность параметров, простоту изменения характеристик, хорошую их повторяемость в процессе про­изводства. При использовании цифровых фильтров не возникает задачи согласования нагрузок, они могут работать в диапазоне от сверхниз­ких частот до частот, измеряемых мегагерцами. Вместе с тем цифровым фильтрам присущи и некоторые специфические особенности, обуслов­ленные цифровым характером обработки сигналов, о Цифровые фильтры используют в системах управления различными объектами и процессами, где алгоритмы обработки могут быть настоль­ко сложными, что аналоговыми устройствами реализованы быть не могут. Другая важная область применения цифровых фильтров — это обработка низко- и инфранизкочастотных сигналов, когда использо­вание аналоговых устройств затруднено из-за больших габаритных размеров катушек индуктивностей и конденсаторов. Области приме­нения цифровых фильтров будут непрерывно расширяться в связи с по­явлением и широким распространением микропроцессоров, специали­зированных БИС ит. п., уменьшением их стоимости и повышением быс­тродействия.

Устойчивость

Во временной области цифровой фильтр устойчив, если его импульсная характеристика удовлетворяет условию (11.18). Теперь определим условия устойчивости цифровых фильтров в -области.

Для этого рассмотрим общую передаточную функцию, заданную выражением (11.40), которое для удобства приведено еще раз:

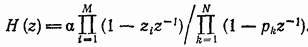
Любой фильтр с передаточными функциями вида (11.163) при называется цифровым фильтром с бесконечной импульсной характеристикой 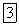поскольку не существует конечного целого числа такого, что

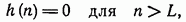
где 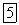— импульсная характеристика фильтра. Для цифровых фильтров положим, что

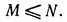
Это предположение верно почти для всех практических случаев. Разложение уравнения (11.163) на простые дроби дает

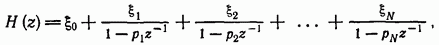
где

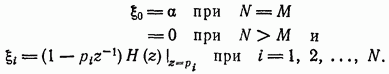
Следовательно, импульсная характеристика, соответствующая выражению (11.163), определяется следующим соотношением:

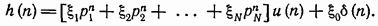
Ясно, что необходимые и достаточные условия того, что импульсная характеристика, заданная выражением (11.167), удовлетворяет критерию устойчивости

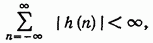
имеют вид .

Это означает, что все полюсы цифрового фильтра расположены внутри единичного круга в z-плоскости.

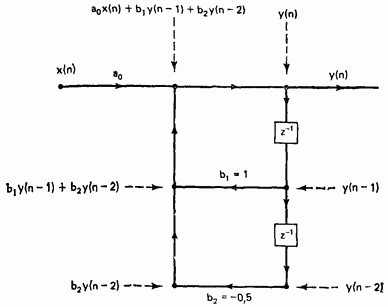
Рис. 11.15. Устойчивая цифровая схема к примеру 11.20.

Пример 11.20. Показать, что схема, приведенная на рис. 11.15, устойчива. Решение. Разностное уравнение, описывающее эту схему, равно

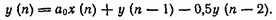
Передаточную функцию схемы можно получить, применив -преобразование к соотношению (11.170):

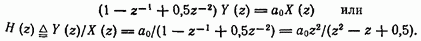
Следовательно, полюсы фильтра расположены в точках

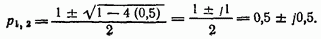
Таким образом, функцию можно переписать в виде

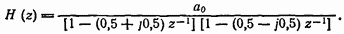
Поскольку

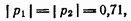
схема на рис. 11.15 устойчива

Если передаточная функция цифрового фильтра представлена в виде

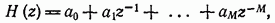
что эквивалентно случаю в выражении (11.163), то цифровой фильтр называют фильтром с конечной импульсной характеристикой (КИХ). Это обозначение используют вследствие того, что импульсная характеристика, соответствующая уравнению (11.175), удовлетворяет следующему условию:

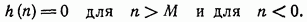
Таким образом, соответствующая импульсная характеристика имеет конечную протяженность. В этом случае отсутствуют полюсы, и поэтому этот тип фильтра всегда устойчив.

Каналы

Непрерывный канал. Это канал связи предназначенный для передачи непрерывных (аналоговых) сигналов. Например, абонентская телефонная линия, канал ТЧ.

Дискретный канал. Совместно с каналом связи УПС образуют дискретный канал, то есть канал, предназначенный для передачи только дискретных сигналов (цифровых сигналов данных).

Различают синхронные и асинхронные дискретные каналы.

В синхронных дискретных каналах ввод каждого единичного элемента производится в строго определенные моменты времени и они предназначены для передачи только изохронных сигналов.

По асинхронному каналу можно передавать любые сигналы - изохронные, анизохронные.

Расширенный канал. Дискретный канал в совокупности с кодером и декодером канала (УЗО) называется расширенным дискретным каналом (РДК).

В технике передачи данных РДК называют каналом передачи данных.

Полунепрерывный канал (дискретный канал непрерывного времени).

В системе ПДС иногда выделяют дискретный канал непрерывного времени.

Для определения выхода данного канала необходимо более детально рассмотреть УПС приема. Он состоит из демодулятора, порогового устройства и регенератора. Выход ПУ одновременно является и выходом дискретного канала непрерывного времени.

Если на выходе дискретного канала имеем сигнал, являющийся дискретной функцией дискретного времени, то на выходе полунепрерывного канала сигнал является дискретной функцией непрерывного времени. (Он же канал постоянного тока).

2. Дискретизация. Квантование. Кодирование. Аналого-цифровые и цифро-аналоговые преобразователи.

Дискретизация — преобразование непрерывной функции в дискретную.

Квантова́ние — процедура построения чего-либо с помощью дискретного набора величин, например, целых чисел, в отличие от построения с помощью непрерывного набора величин, например, вещественных чисел.

Кодирование - в преобразовании полученных измерений сигнала в соответствующие значения некоторого цифрового кода или кодовой комбинации, которые затем передаются по каналам связи.

Аналого-цифровой преобразователь — устройство, предназна­ченное для преобразования непрерывно изменяющейся во времени аналоговой физической величины в эквивалентные ей значения числовых кодов.

Цифро-аналоговый преобразователь — устройство, предназна­ченное для преобразования входной величины, представленной по­следовательностью числовых кодов, в эквивалентные им значения заданной физической величины.

3. Дискретное преобразование Фурье. Свойства ДПФ. Связь спектров аналоговых и дискретных сигналов.

Пара непрерывного преобразования Фурье (интеграл Фурье) имеет вид:

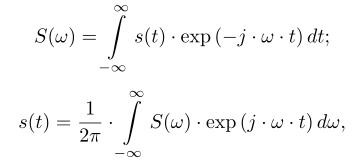
где  — спектр сигнала  (в общем случае и сигнал и спектр — комплексные).

Выражения для прямого ДПФ и обратного дискретного преобразования Фурье (ОДПФ) имеют вид:

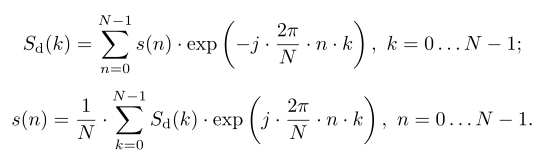
Свойства ДПФ – Линейность ДПФ, ДПФ сигнала с циклическим временным сдвигом, ДПФ циклической свёртки сигналов, ДПФ произведения двух сигналов, Циклический частотный сдвиг, Симметрия ДПФ вещественного сигнала, Частотная инверсия спектра, свойство двойственности.

Связь не стал указывать(большой объём)

4. Восстановление аналогового сигнала.

Для восстановления аналогового непрерывного сигнала необходимо, прежде всего, подать последовательность цифровых отсчетов на ЦАП (рис.), а затем полученный на его выходе электрический дискретный и квантованный сигнал пропустить через ФНЧ.

5. Свёртка. Линейная свёртка. Круговая свёртка.

Свёртка последовательностей — это частный случай свёртки функций. Свёртка является линейным преобразованием входящих в неё последовательностей. Свёртку двух заданных последовательностей можно получить, если, сначала, использовать для каждой последовательности дискретное преобразование Фурье (ДПФ), затем перемножить результаты преобразования и произвести обратное дискретное преобразование Фурье (обратное ДПФ).

Для получения круговой свертки (периодической) необходимо представить, что две последовательности располагаются на двух окружностях. Одна окружность находится внутри другой. Значения каждой из этих последовательностей равноудалены друг от друга. Для получения каждого значения круговой свертки необходимо представить, что одна из последовательностей движется по окружности относительно другой по часовой стрелке. К примеру, возьмем первое значение последовательности, которая вращается, последовательно умножим на значения другой последовательности и просуммируем результаты умножений — так получим первое значение выходной последовательности, которое было получено при помощи круговой свертки. Данные действия повторить для каждого значения последовательности, которая вращается относительно другой. Количество элементов в выходной последовательности будет равно количеству элементов последовательности, которая вращается.

Для расчёта линейной свертки необходимо выполнить такую последовательность действий:

произвести расчёт количества элементов выходной последовательности по формуле:



где:

 — количество элементов в выходной последовательности;

 — количество элементов в первой последовательности;

 — количество элементов во второй последовательности;

дополнить нулями обе последовательности так, чтобы количество элементов в этих последовательностях была равна  ;

симметрично отобразить одну из последовательностей относительно оси ординат;

произвести перемножение этих двух последовательностей.

В результате выполнения всех описанных выше операций получим линейную свёртку двух последовательностей.