Характеристики САУ. Переходная функция.

Характеристики САУ

Выходной сигнал любой детерминированной системы зависит от входного сигнала, данному входному сигналу соответствует один вполне определенный выходной сигнал. Иными словами, выходной сигнал данной детерминированной системы является вполне определенной функцией ее входного сигнала. Однако функцию надо в данном случае понимать не в том смысле, как она понимается в элементарном математическом анализе, а в обобщенном смысле, так как аргументом функции в данном случае служит некоторая функция времени — входной сигнал системы, а значением функции при данном значении аргумента (входном сигнале) тоже служит некоторая функция времени — выходной сигнал системы.

В современной математике функцией называется в общем случае однозначное соответствие между любыми объектами — элементами некоторых множеств. А именно функцией называется такое соответствие между элементами двух множеств X и У, когда каждому элементу х множества Xсоответствует один вполне определенный элемент у множества Y. При этом элементами множеств Xи Yмогут быть любые объекты. В частности, ими могут быть скалярные или векторные функции любых переменных.

Математическое описание линейного непрерывного динамического элемента системы сводится к описанию связи между его входом и выходом. Данная связь может быть задана в виде: 1) линейного дифференциального уравнения; 2) передаточной функции; 3) частотных характеристик; 4) временных характеристик; 5) переменных состояния.

1) Как уже отмечалось, распространенной формой описания линейных непрерывных ДЭ (ДС) являются линейные дифференциальные уравнения.

Например: 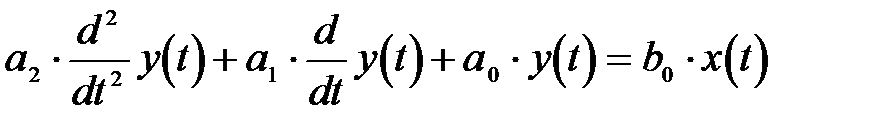- во временной области;

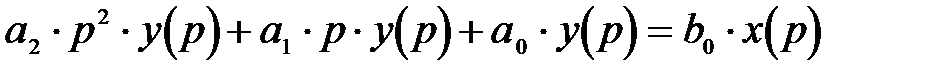- в области изображений по Лапласу.

2) Передаточная функция ДЭ равна отношению изображения по Лапласу выходного сигнала y(p) к изображению входного воздействия x(p) при нулевых начальных условиях .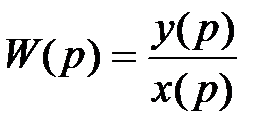

3) Частотной характеристикой АС - называется ее реакция на входной гармонический сигнал произвольной частоты.

4) Под временными характеристиками понимают реакцию АС на типовое задающее воздействие. Различают две временные характеристики импульсную (весовую) и переходную.

5) Под переменными состояния понимают минимальный набор переменных, который в данный момент времени вместе со значениями входных переменных определяет поведение системы во все последующие моменты времени.

Переходая функция

Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент t=0 . Формально этот сигнал определяется так:

Реакция объекта на единичный скачок называется переходной функциейи обозначается h(t):

При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.

Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состояний. Это значит, что переходная характеристика дает меньше информации, чем исходные уравнения.

Пусть модель объекта задана дифференциальным уравнением первого порядка:

где k – безразмерный коэффициент, а T – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая уравнение (16) при x(t)=1(t>0), получаем

где постоянная C₁должна определяться из начальных условий. Поскольку нас интересует переходная характеристика, начальные условия считаем нулевыми, то есть y(0)=0, что дает C₁=−k и поэтому

На рисунке показаны переходные характеристики (17) при различных значениях параметра T, который называется постоянной временизвена:

Видно, что при увеличении T выход y медленнее достигает установившегося значения, равного k , то есть постоянная времени характеризует инерционность звена (16). Чем больше постоянная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.

Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.