Представим передаточную функцию как

W =f₁(p)/f₂(p)

Рассмотрим W = f₁/pf₂ = (1/p)f₁/f₂ Первая математическая форма f₁/pf₂ подразумевает ускорение формирования выходного сигнала за счёт дифференцирующего звена. Вторая математическая форма - (1/p)f₁/f₂ - замедление входного сигнала (или помехи) за счёт интегрирующего звена. Эквивалентность этих математических форм означает что для борьбы с помехами могут использоваться обе эти формы. Отметим, что ускорение или замедление соответствующих сигналов с физической точки зрения означает изменение их спектральных характеристик.

Типичным примером минимизации аддитивных помех (например, в системах питания) является использование второй математической формы (интегрирующего звена - емкостей) по соответствующим цепям питания. Это позволяет разнести спектральные характеристики сигналы и помехи.

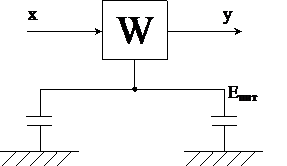
Перечисленные свойства систем управления обычно определяют как показатели качества соответствующей системы. В эти показатели входят, как правило, устойчивость, точность, характер переходных процессов (монотонный или колебательный).

В ряде случаев при колебательных переходных процессах показатель перерегулирования (выброс процесса) имеет самостоятельный смысл и нормируется в качестве дополнительного свойства системы.

Пример синтеза и анализа типичной системы управления.

В качестве примерарассмотрим курсовой канал автопилота в упрощённом виде.

ЛА — направление движения летательного аппарата;

N, S — ось север- юг;

ψ — заданный угол, то есть условное положение объекта регулирования относительно оси NS;

I — момент инерции ЛА;

M₀ — внешний возмущающий момент (помехи);

M_упр — управляющий момент, воздействующий на ЛА со стороны автопилота.

Формулировка задачи управления

Поддерживать заданный курсовой угол ψ ЛА с определённой точностью, путём формирования в системе автопилота M_упр при воздействии M₀.

Запишем уравнение движения ЛА на основе уравнений механики

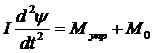
При синтезе автопилота необходимо задать следующие уравнения:

а) 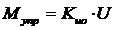, где K_ио — коэффициент передачи исполнительных органов ЛА, U — сигнал управления, формирующийся на основе следующего закона управления в виде PD-регулятора

б)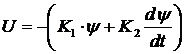

PD-регулятор включает пропорциональную составляющую K₁ψ и дифференциальную составляющую 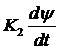, включённую для ускорения процесса управления. Знак минус означает, что сигнал управления должен быть противоположен отклонению оси ЛА от заданного угла ψ. Тогда получим

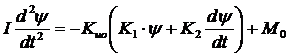или

[Iр² + (К₁ + К₂р)К_ио] ψ = М₀

Рассмотренные математические формы являются дифференциальными уравнениями движения ЛА с учётом действий автопилота с определённым законом управления.

Рассмотрим ту же задачу синтеза с позиции передаточных функций.

а) Передаточная функция ЛА

ψ = ( М_упр + М₀)/ Iр²

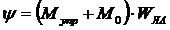
W_ла = 1/ Iр²

б) Передаточная функция регулятора и исполнительного органа: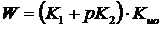

в) Обратная связь: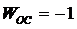

На основе полученных передаточных функций представим структуру системы управления ЛА и рассмотрим ее математическую модель

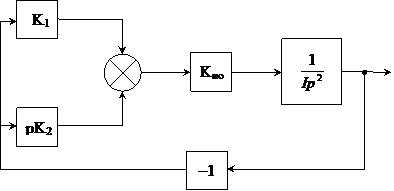
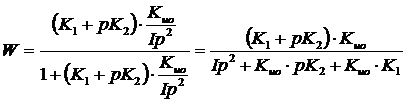
Очевидно, что характеристические уравнения, полученные в дифференциальной форме и на основе передаточных функций, полностью совпадают, что соответствует эквивалентности данных процедур синтеза. На этом этапе исходная задача синтеза завершена. Мы получили требуемую структуру системы. На следующем этапе синтеза необходимо ввести определённые ограничения на параметры структуры. Для этого необходимо решить соответствующие задачи анализа.

а) Задача анализа устойчивости:

Из соответствующего характеристического уравнения запишем условия устойчивости

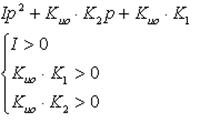
Проанализируем эти условия устойчивости:

I — известно для конкретного типа ЛА,

K_ио — известно для конкретного типа ЛА,

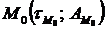— известно для определенных условий движения ЛА, где

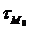— временные параметры возмущающего момента

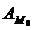— амплитудные параметры возмущающего момента

Если временные и амплитудные параметры момента М₀ неизвестны, то построить систему управления, эффективную для такого рода воздействий, невозможно.

Из последнего известного условия следует, что динамические свойства системы управления должны определённым образом соответствовать временным параметрам М₀. То есть ;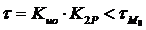

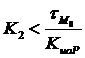
б) Задача анализа точности.

Из дифференциального уравнения при условии р = 0 получим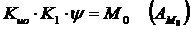

при условии 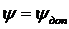получим

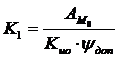
Таким образом, на основе решения задач анализа завершена процедура синтеза данной системы управления.

Таким образом, разработанная система управления (автопилот) решает задачу поддержания заданного курсового угла определённого ЛА с заданной точностью, при этом система будет устойчивой.

Рассмотрим особенности управления ЛА пилотом и сравним их с автопилотом:

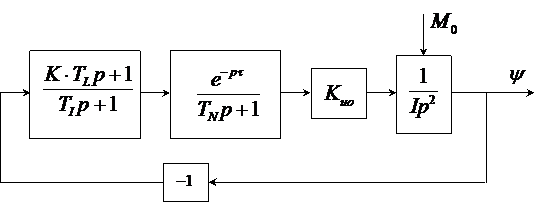
Сравнивая две структуры систем управления, можно сделать выводы:

во-первых, динамические свойства автопилота лучше динамических свойств пилота;

во-вторых, автоматические системы имеют ограниченную работоспособность и эффективность в условиях априорной неопределённости возмущающих факторов. В этом смысле пилот-оператор оказывается более эффективным.

Рассмотрим особенности применения ЭВМ в системах управления вообще и в автопилоте в частности.

Основной особенностью ЭВМ является принципиальная возможность формирования любых законов управления. В частности, функции PID – регуляторов реализуются на основе численных методов интегрирования и дифференцирования. Кроме функций регулятора, ЭВМ могут выполнять другие функции, например функции сравнения априорной и апостериорной информации, борьбы с помехами, формирования заданных показателей точности и областей устойчивости за счет программной вариации параметров регулятора (адаптивное управление). Поэтому очевидна целесообразность применения средств вычислительной техники в системах управления. В частности, в современных автопилотах функции регулятора выполняют ЭВМ с использованием АЦП и ЦАП.