Тема: Табличное умножение и деление
План:
1. Подготовительный этап к изучению табличного умножения и деления:
- упражнения на нахождение суммы одинаковых слагаемых;
- ознакомление с конкретным смыслом умножения и терминологией;
- изучение перестановки множителей и применение этого правила в вычислениях;
- таблица умножения с числом 2;
- ознакомление с конкретным смыслом действия деления по содержанию, деление на равные части и с терминологией;
- обобщение двух видов деления;
- изучение взаимосвязи между результатом и компонентом действий умножения и деления.
2. Методика изучения табличных случаев умножения и деления.
3. Альтернативные подходы к изучению умножения и деления.
Рекомендательная литература
1. Вершинин Н.Я. Игры при изучении табличных случаев деления и умножения // Начальная школа. – 1987. - №2. – С. 38-39.
2. Истомина Н.Б. Методика обучения математике в начальных классах. – М.: ЛИНКА-ПРЕСС, 1997. – 288 с.
3. Методическая копилка // Начальная школа. – 1998. - №2.
4. Никулина А.Д. Изучение табличного умножения и деления // Начальная школа. – 1987. - №10. – С. 42.
5. Пиядин Н.С. Умножение и деление в новой дидактической системе обучения // Начальная школа. – 1997. - №7. – С. 26-34.
6. Серебрянникова Л.С. Я учу таблицу // Начальная школа. – 1997. - №5. – С. 67-72.
7. Туркина В.М. Работа по составлению таблицы умножения // Начальная школа. – 1987. – 1998. - №5. – С. 58.
8. Унгру Ю.П. Пособие для изучения таблиц сложения и умножения // Начальная школа. – 1987. - №5. – С. 42-43.
9. Урок в системе развивающего обучения: из опыта работы / под ред. Дусавицкого А.К. – Харьков, 1998. – 61 с.
10. Уткина Н.В. Таблица умножения // Изучение трудных тем по математике в 1-3 классах / Сост. Н.Г.Уткина. – М.: Просвещение, 1982.
Новые арифметические действия умножения и деления вводятся в четвертой четверти 2 класса. Основная задача в этот период состоит в том, чтобы ребенок понял конкретный смысл этих действий.
Так как умножение является частным случаем сложения, то данную работу можно провести следующим образом. Предлагаем ребенку 7-8 различных сумм, среди которых 2-3 состоят одинаковых слагаемых:
2 + 3 + 4 = 5 + 5 = 3 + 3 + 3 + 3 =
3 + 3 + 7 = 9 + 4 = 7 + 5 + 3 =
Сравнивая между собой эти суммы, выделяем те из них, которые состоят из одинаковых слагаемых. После этого можно объяснить, что в математике такие суммы записываются более кратко: сначала пишется число, которое складывается, затем пишется число, равное количеству слагаемых, и между ними ставится точка, обозначающая новое действие – умножение:
5 + 5 = 5 · 2 (но не 2 · 5);
3 + 3 + 3 + 3 = 3 · 4;
7 + 7 + 7 = 7 · 3.
Убедившись, что ребенок понял смысл умножения, ему можно предложить потренироваться в замене сложения умножением и наоборот.
Так же как и у других действий, у умножения каждое число имеет свое «имя»:
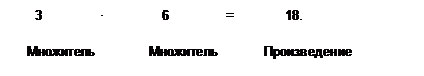
После усвоения конкретного смысла умножения можно перейти к следующему действию – делению. Различают два вида деления: 1) деление по содержанию; 2) деление на равные части. Приведем примеры этих видов деления:
| Деление по содержанию | 6 карандашей разложили в коробки, по 2 карандаша в каждую. Сколько потребовалось коробок? |
| Деление на равные части | 6 карандашей разложили поровну в 3 коробки. Сколько карандашей в каждой коробке? |
Знакомство с действием деления лучше начинать с деления по содержанию на основе практических действий с предметами усваивается конкретный смысл деления, показывается его запись. После этого можно перейти к делению на равные части.
Правила нахождения неизвестных компонентов умножения и
деления
Правило нахождения неизвестных множителя, делимого и делителя изучаются по одной и той же схеме в начале 3 класса: 1) на основе практической задачи составляется пример на умножение или деление; 2) к нему подбираются два взаимно-обратных примера; 3) на основе соотнесения названий компонентов в этих взаимно-обратных примерах выводятся соответствующие правила.
Рассмотрим это на примере правила нахождения неизвестного множителя.

1) 4 · 3 = 12;
2) 12 : 4 = 3;
3) 12 : 3 = 4.
Так как 3 и 4 – это множители, а 12 – произведение, то из 2) и 3) легко выводится правило:
Если произведение двух чисел разделить на один из множителей, то получится другой множитель.
Аналогично выводятся правила нахождения неизвестного делимого и делителя.
Табличное умножение и деление
Табличное умножение и деление является центральной темой 3 класса. От того, насколько у ребенка будут успешно сформированы навыки в пределах табличных случаев, во многом зависит процесс дальнейшего освоения арифметических действий. Табличное умножение и деление к концу 3 класса должно быть отработано до автоматизма. Для сокращения количества случаев табличного умножения и деления предварительно изучается переместительное свойство умножения. Это позволяет после знакомства, например, со случаем 3 · 8 не рассматривать отдельно случай 8 · 3, т.к. 3 · 8 = 8 · 3.
Изучение всех случаев табличного умножения и деления от 2 до 9 равномерно рассредоточено в течение длительного времени и осуществляется по одному и тому же плану. Поэтому мы ограничимся рассмотрением этой темы на примере числа 4.
В подготовительный период нужно хорошо отработать следующие вопросы: понимание конкретного смысла действий умножения и деления; название компонентов и результатов этих действий и правило нахождения неизвестного множителя; переместительное свойство умножения; счет «четверками».
Эти опорные знания используются при составлении следующих четырех столбиков примеров:
| 4 · 4 = | 16 : 4 = | |||||
| 4 · 5 = | 5 · 4 = | 20 : 4 = | 20 : 5 = | |||
| 4 · 6 = | 6 · 4 = | 24 : 4 = | 24 : 6 = | |||
| 4 · 7 = | 7 · 4 = | 28 : 4 = | 28 : 7 = | |||
| 4 · 8 = | 8 · 4 = | 32 : 4 = | 32 : 8 = | |||
| 4 · 9 = | 9 · 4 = | 36 : 4 = | 36 : 9 = |
Результаты первого столбика находятся на основе перехода от умножения к сложению:
4 · 4 = 4 + 4 + 4 + 4 = 16;
4 · 5 = 4 · 4 + 4 = 16 + 4 = 20;
………..............
4 · 9 = 4 · 8 + 4 = 32 + 4 = 36.
Результаты второго столбика составляются на основе первого столбика с использованием переместительного свойства умножения («так как 4· 7 = 28, то и 7 · 4 = 28»).
Результаты третьего и четвертого столбиков также составляются на основе первого столбика с использованием правила нахождения неизвестного множителя: «Если произведение 20 разделить на первый множитель 4, то получится второй множитель - 5». Только разобравшись со способами нахождения результата для каждого примера, можно переходить к заучиванию таблицы умножения и деления наизусть.
