Пропорциональными величинами

План:

1. Упражнения в учебнике, приводящие к понятиям «прямая и обратная зависимость».

2. Формирование представлений о прямопропорциональной и обратнопропорциональной зависимости.

3. Простые задачи с тройкой пропорциональных величин и особенности работы с ними.

4. Составные задачи с пропорциональными величинами:

а) составные задачи, содержащие в качестве одной из простых задачи с тройкой пропорциональных величин;

б) задачи на нахождение четвертого пропорционального;

в) задачи на пропорциональное деление;

г) задачи на нахождение неизвестного по двум разностям.

Рекомендательная литература

1. Скаткин Л.Н., Жигалкина Т.К. Обучение решению задач с пропорциональными величинами. – М.: Просвещение, 1979. – 32 с.

2. Гребенникова Н.Л. Решение задач на зависимость величин различными способами // Начальная школа. – 1999. - №2. – С. 45-49.

3. Казько Е.С. Работа с текстом задачи с пропорциональными величинами // Начальная школа. – 1998. - №5. – С. 70-74.

В начальных классах дети знакомятся с тройками пропорциональных величин: цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и т.д. С этими величинами можно особо выделить 3 вида составных задач: на нахождение четвертого пропорционального; на пропорциональное деление; на нахождение неизвестного по двум разностям. Первый из этих видов вводится в 3 классе, а второй и третий – в 4 классе, рассмотрим особенности работы над задачами на нахождение четвертого пропорционального с величинами: цена, количество, стоимость.

На подготовительном этапе в ходе решения простых задач отрабатываются правила нахождения одной из величин по двум другим, пропорциональным ей: например, как найти цену, зная стоимость и количество. После этого можно перейти к решению составных задач.

Текст задачи

За 5 метров ткани заплатили 40 рублей. Сколько стоят 7 метров такой же ткани?

Краткая запись условия

Запись условия задач с пропорциональными величинами оформляется в виде таблицы:

Цена	Количество	Стоимость
Одинаковая	5 м 7 м	40 р. ?

Разбор

На начальном этапе разбор таких задач осуществляется аналитическим способом:

- Что известно в задаче? (Что за 5 метров ткани заплатили 40 рублей.)

- Что еще дано в условии задачи? (7 метров такой же ткани.)

- Какой главный вопрос задачи? (Сколько стоят 7 метров такой же ткани?)

- Можем ли мы сразу ответить на главный вопрос задачи? (Нет.)

- Что для этого нужно знать? (Для того, чтобы найти стоимость, нужно знать цену и количество.)

- Количество известно, а что сказано про цену? (Что она одинаковая.)

- Как же найти цену по стоимости и количеству? (Нужно стоимость (40 р.) разделить на количество (5 м.))

- Найдя цену, как узнаем стоимость 7 метров ткани? (Цену умножим на количество метров.)

Запись решения

1 способ – по действиям с пояснением:

1) 40 : 5 = 8 (р.) – стоит 1 м ткани.

2) 8 · 7 = 56 (р.) – стоят 7 м ткани.

Ответ: 56 рублей

2 способ – составлением выражения:

40 : 5 · 7 = 56 (р.)

Ответ: 56 рублей

В дальнейшем от аналитического способа разбора можно переходить к синтетическому, а краткую запись условия можно сделать более компактной:

5 м – 40 р.

7 м - ?

Наиболее сложными задачами, которые изучаются в з классе, являются задачи, связанные с пропорциональными величинами. Рассмотрим решение этих задач на примере задачи на нахождение неизвестных по двум разностям и задачи на пропорциональное деление.

Вид задачи	На пропорциональное деление
Условие	В магазин привезли 6 ящиков картофеля и 4 таких же ящика свеклы. Всего в магазин привезли 120 кг овощей. Сколько килограммов картофеля и сколько килограммов свеклы привезли в магазин?
Краткая запись условия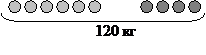
Разбор задачи	Аналитический способ разбора: 1) Что известно в задаче? 2) Что нужно узнать в задаче? 3) Можем ли мы сразу ответить, сколько килограммов картофеля привезли в магазин? (Нет.) 4) Что для этого нужно знать? (Массу одного ящика и количество ящиков.) 5) Количество ящиков известно, а как можно найти массу одного ящика? (Общую массу разделить на общее количество ящиков.) 6) Как приведем общее количество ящиков? (К 6 прибавим 4.) 7) Узнав массу одного ящика, как найдем массу всего картофеля? (Массу одного ящика умножим на количество ящиков с картофелем.) 8) Как узнать массу всей свеклы? (Массу одного ящика умножим на количество ящиков со свеклой.) 9) Как можно другим способом узнать массу всей свеклы? (из общей массы вычесть массу картофеля.)
Запись решения	Запись решения по действиям с пояснением: 1) 6 + 4 = 10 (ящ.) – привезли всего. 2) 120 : 10 = 12 (кг) – масса одного ящика. 3) 12 · 6 = 72 (кг) – привезли картофеля. 4) 12 · 4 = 48 (кг) – привезли свеклы. Ответ: 72 кг и 48 кг.
Вид задачи	Нахождение неизвестных по двум разностям
Условие	В магазин привезли 6 ящиков картофеля и 4 таких же ящика свеклы, причем картофеля привезли на 24 кг больше, чем свеклы. Сколько килограммов картофеля и сколько килограммов свеклы привезли в магазин?
Краткая запись условия	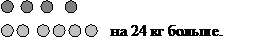Из этой наглядной записи хорошо видно, что 24 кг картофеля находятся в 2 ящиках.
Разбор задачи	Синтетический способ: 1) Что известно в задаче? 2) Что нужно узнать в задаче? 3) Почему картофеля оказалось в магазине на 24 кг больше (Потому, что ящиков с картофелем было больше.) 4) На сколько ящиков больше? (на 2.) 5) Какой вывод из этого можно сделать? (Что 24 кг картофеля находится в 2 ящиках.) 6) Зная это, как найти массу одного ящика с картофелем? (Нужно 24 кг разделить на 2.) 7) Как теперь найти массу картофеля и массу свеклы? (Массу одного ящика умножить на количество ящиков.)
Запись решения	Запись решения с предварительной постановкой вопросов: 1) На сколько ящиков картофеля привезли больше, чем свеклы? 6 – 4 = 2 (ящ.) 2) Какова масса одного ящика с овощами? 24 : 2 = 12 (кг) 3) Сколько килограммов картофеля привезли в магазин? 12 · 6 = 72 (кг) 4) Сколько килограммов картофеля привезли в магазин? 12 · 4 = 48 (кг) Ответ: 72 кг картофеля и 48 кг свеклы.