Произвольные системы m линейных уравнений с n неизвестными. Понятие общего, частного и базисного решений системы уравнений.

Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:

,

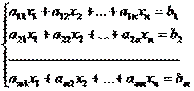где a_ij – коэффициенты, а b_i – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Определение. Для системы линейных уравнений матрица

А = называется матрицей системы, а матрица

А*= 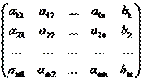называется расширенной матрицей системы

Определение. Если b₁, b₂, …,b_m = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение.

Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

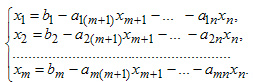
Частным решением системы уравнений называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

• Базисное решение (вектор) называется вырожденным, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
• Базисное решение называется невырожденным, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

32.Метод Жордана-Гаус­са.

Переход от одного базисного решения к другому. ( не нашел, к сожалению)

Понятия опорного и допустимого решений систем линейных уравнений.

Решение системы m-линейных уравнений с n-неизвестными, в которых значения всех переменных неотрицательны называются допустимыми решениями, а совокупность всех допустимых значений областью допустимых решений. Базисные допустимые решения называются опорными решениями, число которых решений меньше числа базисных.

35.Симплексные преобразования. Теорема о симплексных преобразованиях.

Переход от одного опорного решения к другому.

Общая задача оптимизации.

Типы задач математического программирования: линейное программирование, нелинейное программирование, динамическое программирование.

Оптимизационные задачи, в которых приходится учитывать последовательность действий или фактор времени, рассматриваются в разделе динамического программирования. В отличие от предыдущих задач математического программирования задачи динамического программирования являются многоэтапными или многошаговыми.