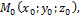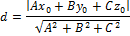Кривые второго порядка.Окружность. Эллипс. Гипербола. Парабола.

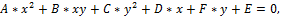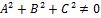Линия называется кривой 2го порядка, если уравнение ее содержит переменные x,y во 2ых степенях либо их произведение (x*y). Общий вид уравнения кривой 2го порядка: где . Геометрическим местом точек называется совокупность точек, обладающих одними и теми же общими для них свойствами. К кривым 2го порядка относятся: окружность, эллипс, гипербола и парабола.

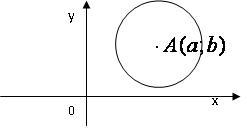
Окружность.Окружность – это множество точек плоскости, равноудаленных от данной точки (центра).

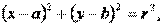где 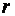- радиус окружност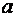и, и 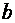- координаты центра окружности.

Если центр окружности совпадает с началом координат, то уравнение имеет вид: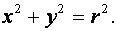

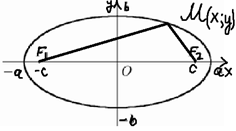
Эллипсомназываетсягеометрическое множество точек, сумма расстояний которых до 2х данных точек называется фокусами есть величина постоянная равная 2а, где а>0.

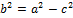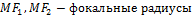. . Обозначение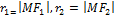

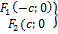фокусы

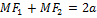
Расстояние от точки М до фокусов эллипса называется фокальным радиусом: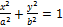

Каноническое уравнение элипса. Если a>b, то a-большая полуось, b-малая. Если a<b, то a-малая, b-большая. Расстояние между фокусами называется фокальным, и это расстояние = 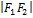=2c

Фокусы всегда располагаются на большое оси э. Если a>b, то c= 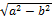. Если a<b, то 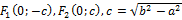. Если b=a, то получим окружность, фокусы при этом сольются в 1ой точке, в центре окруж-ти. Эксцентриситет-показ-ль, характеризующий степень деформации окружности, при которой получится э. Эксцентриситетом эллипса наз-ся отношение фокального расстояния 2с к длине большой оси: , .

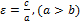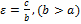Эксцентриситет эллипса всегда <1, а эксцентриситет окруж-ти =0. Фокальный радиус эллипса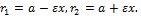

Гипербола.

Г. наз-сягеометрическое множество точек, сумма расстояний от которых до 2х данных точек наз-ся фокусами есть величина постоянная равная 2а.

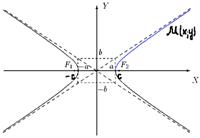а-точка пересечения по Ox. .

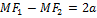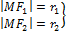– фокальные радиусы

Каноническое уравнение Г. имеет вид: 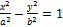, где .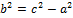

Свойства гиперболы:

1) Симметрична относит-но обеих осей координат.

2) Точка пересечение Г. с осью абсцисс наз-сядействительыми вершинами Г. Координаты имеют вид (a;0) (-a;0). Точки на оси ординат (0;b) (0;-b) – наз-ся мнимыми вершинами Г.

3) Ось абсцисс наз-ся действительной осью Г., а ось ординат-мнимой. a-действительная полуось, b-мнимая

4) Фокусы Г. – 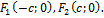Они всегда расположены на действительной оси, поэтому действит.ось иногда наз-ся фокальной. Расстояние между фокусами = 2с,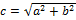

5) Отношение фокального расстояния 2с к длине действит.оси 2а наз-ся эксцентриситетом гиперболы, т.е.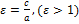

6) Если b=a, то Г.наз-ся равнобочной: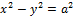

7) Асимптоты кривой y=f(x) наз-ся прямая y=kx+b, к которой неограничено приближаются ветви кривой при удалении ее точек в бесконечность. Прямые 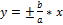явл-ся асимптотами Г.

8) Фокальные радиусы находятся как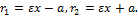

9) Если ур-ие Г. Задать в виде формулы 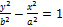, то мнимой осью будет ось абсцис, а действительной-ось ординат. Фокусы будут расположены на оси ординат и иметь координаты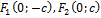

Парабола

П. наз-сягеометрич. место точек, равноудаленных от данной точки называемой фокусом, и от данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы наз-ся параметром параболы, и обознач-ся через p. 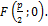А уравнение директрисы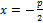

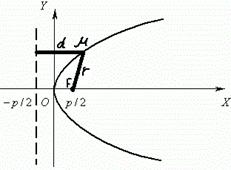
d-расстояние от точки М до директрисы. r-фокальный радиус

Уравнение параболы каноническое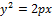

Свойства:

1) Обл.опред-ия[0;+∞)

2) Обл.значения (-∞;+∞)

3) Ветви направленны вправо

4) Вершина (0;0)

5) Парабола симетрична относит-но оси Ох

6) Эксцентриситетом П.наз-ся отношение фокального радиуса точки М к расстоянию d, от точки Ь до директрисы, т.е.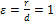

7) Фокальный радиус П.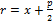

Общее ур-ие П: 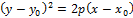– график1

Вершины параболы .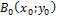

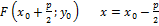
Если фокус лежит левее директрисы, то уравнение параболы 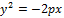– график2

Если фокус выше директрисы, то – график3 ( )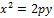

Если фокус ниже директрисы то – график4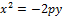

16.Прямая и плоскость в трехмерном пространстве и способы их задания. Взаимное расположение прямой и плоскости в пространстве.

Плоскость в трехмерном пространстве и способы ее задания:

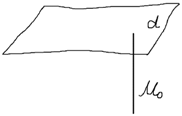
Пусть дана плоскость в пространстве р. Любую плоскость в пространстве можно задать точкой 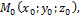лежащей на этой плоскости и ненулевым вектором 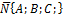( 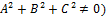, перпендикулярным этой плоскости.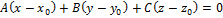

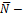нормальный вектор плоскости (нормаль)

Ax+By+Cz+D=0 – общее уравнение плоскости

Рассмотрим 2 плоскости 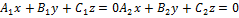. Нормаль у 1ой плоскости 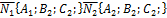. Угол между плоскостями равен углу, образованному между векторам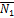и и .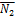

Cos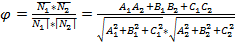

Две плоскости параллельны только тогда, когда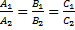

Две плоскости перпендикулярны, когда 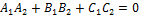(скалярное произведение 2х векторов).

Если выполняется условие 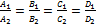, то плоскости сливаются

Плоскость р задается, если дана точка 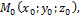лежащая на плоскост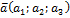и и 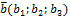, лежащие на плоскости и имеющие начало точку 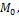векторы и не коллинеарны.

Уравнение плоскости: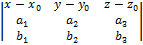

Прямая в трехмерном пространстве и способы ее задания:

Рассмотрим прямую в пространстве l. Она задается точкой 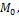которыя лежит на этой прямой и вектором 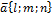-направляющий вектор. Тогда уравнение прямой

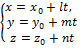
Параметрическое уравнение прямой t-некоторый параметр t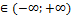

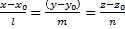– каноническое уравнение прямой

Пусть даны 2 точки 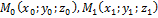тогда уравнение прямой имеет вид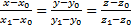

Прямую в пространстве можно задать как линию пересечения 2х плоскостей:

(1)

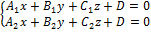
Для того, чтобы найти точку 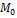, необходимо решить (1). Один из неизвестных можно задать произвольны значением. находится как векторное произведение нормальных векторов.

Пусть даны 2 прямые ,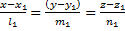

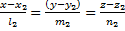
Углом 2х прямых наз-ся любой из 2х углов, образуемых 2мя прямыми соответственно параллельными данным прямым и проходящими через 1 точку

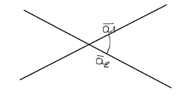
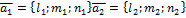
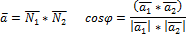
Две прямые перпендикулярны тогда и только тогда, когда выполняется следующее равенство

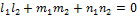
Две прямые параллельны тогда и только тогда, когда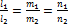

Взаимное расположение прямой и плоскости в пространстве:

Пусть дана плоскость Ax+By+Cz+D=0