Основные законы применяемые для составления описания элементов САР. Уравнение емкости, как объекта управления.
Для получения описаний уравнений элементов используются физические законы, определяющие их поведение в системе. Обычно такими законами являются:
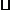 второй закон Ньютона в виде
второй закон Ньютона в виде
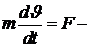 для описания прямолинейного движения тела (m – масса, F – движущая сила,
для описания прямолинейного движения тела (m – масса, F – движущая сила, 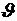 - линейная скорость движения ), а также для описания вращательного движения тела в виде
- линейная скорость движения ), а также для описания вращательного движения тела в виде
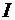
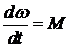 - для описания вращательного движения,
- для описания вращательного движения,
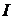 - момент инерции вращающейся массы,
- момент инерции вращающейся массы, 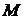 - вращающий момент,
- вращающий момент, 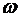 - угловая скорость);
- угловая скорость);
 закон сохранения энергии в виде
закон сохранения энергии в виде 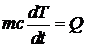 - для описания изменения температуры тела
- для описания изменения температуры тела 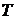 c массой
c массой 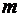 и удельной теплоемкостью «
и удельной теплоемкостью « 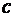 » под действием теплового потока
» под действием теплового потока 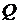 ;
;
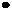 уравнение состояние газа в виде
уравнение состояние газа в виде 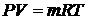 - для установления математической связи давления газа
- для установления математической связи давления газа 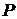 , его температуры
, его температуры 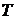 и объема
и объема 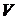 физически однородной системы в состоянии термодинамического равновесия (R – газовая постоянная,
физически однородной системы в состоянии термодинамического равновесия (R – газовая постоянная, 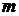 - масса газа).
- масса газа).
Кроме указанных применяются и другие законы физики, например, устанавливающие связь между электрическими переменными и параметрами различных электромеханических устройств, применяемых в системах управления и т. д.
Математическое выражение физического закона, который описывает процесс, протекающий в данном элементе, является исходным уравнением.
Рассмотрим пример. Пусть требуется получить уравнение для емкости с газом, рис.1. При этом емкость будем рассматривать как объект, в котором требуется регулировать давление газа. Обозначим через Рг, Тг и Vг соответственно давление, температуру и объем газа в емкости. Массовые расходы газа в емкость и из емкости обозначим соответственно символами GП и GB.
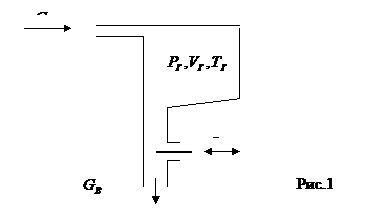
Исходным уравнением, отражающим термодинамическое равновесное состояние газа в емкости, служит уравнение состояния
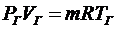 . (1.9)
. (1.9)
Дополняющими уравнениями являются зависимости, определяющие расходные характеристики:
Можно упростить, считая, что Tг = соnst и ς = сonst. В этом варианте можем записать, что :
GП = fП ( Рг); (1.10)
GВ = fВ (Рг , r).
Расходные характеристики часто задаются в виде экспериментальных зависимостей. В данном случае эти характеристики являются нелинейными и имеют вид некоторых условных кривых, представленных на рис.
|

Для составления уравнения емкости запишем уравнение состояния в виде
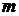 =
= 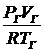 . Далее можно записать
. Далее можно записать 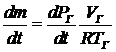 . Последнее выражение также соответствует записи
. Последнее выражение также соответствует записи 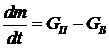 . Приравнивая правые части двух равенств , получим искомое уравнение
. Приравнивая правые части двух равенств , получим искомое уравнение
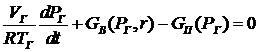 (1.11)
(1.11)
Так как зависимости GB и GП нелинейные (см.рис.), то и полученное уравнение является нелинейным. Уравнение (1.11) можно записать в символическом виде
F ( 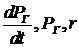 ) = 0. (1.12)
) = 0. (1.12)
Видно, что в данном уравнении две переменные: 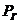 и
и 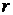 . Так как емкость рассматривается как объект регулирования, то можно утверждать, что давление газа
. Так как емкость рассматривается как объект регулирования, то можно утверждать, что давление газа 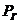 в емкости является регулируемой величиной, а перемещение заслонки
в емкости является регулируемой величиной, а перемещение заслонки 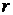 - регулирующим воздействием.
- регулирующим воздействием.
5. Формы записи линеаризованных уравнений..
|
|
|
|


Первая форма записи.
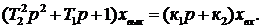 (1.19)
(1.19)
В уравнении коэффициенты 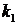 и
и 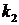 называют коэффициентами передачи, а коэффициенты
называют коэффициентами передачи, а коэффициенты 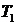 и
и 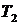 постоянными времени. В случае элементов, у которых переменные
постоянными времени. В случае элементов, у которых переменные 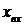 и
и 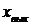 имеют одинаковые размерности для коэффициентов
имеют одинаковые размерности для коэффициентов 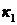 и
и 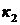 используются и другие названия:
используются и другие названия:
коэффициент усиления - для усилителей сигналов;
передаточное число – для редукторов, делителей напряжения и др
Постоянные времени 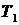 и
и 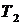 имеют размерность времени. Размерности коэффициентов передачи
имеют размерность времени. Размерности коэффициентов передачи 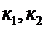 связаны с размерностями переменных
связаны с размерностями переменных 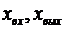 и могут быть определены из уравнения (1.19). Оператор дифференцирования
и могут быть определены из уравнения (1.19). Оператор дифференцирования 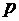 имеет размерность
имеет размерность 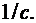
Вторая форма записи.В теории автоматического регулирования широко применяется понятие передаточной функции.
Передаточной функцией САР или другого какого-либо устройства называется отношение преобразования Лапласа выходной величины к преобразованию Лапласа входного сигнала при нулевых начальных условиях.
Передаточная функция является второй формой записи дифференциальных уравнений элементов САР. Например, уравнение
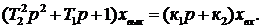
в этой форме должно иметь вид
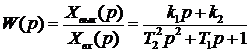 . (1)
. (1)
Из этого же уравнения следует, что
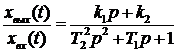 . (2)
. (2)
Видно, что при нулевых начальных условиях отношение изображений Лапласа входного и выходного сигналов (1) совпадает с отношением их оригиналов (2). Поэтому в теории управления последнюю запись принимают за передаточную функцию, считая ее второй формой записи..
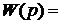
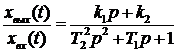
Группы динамических звеньев
|
1.Позиционные звенья;
2.Дифференцирующие и интегрирующие звенья;
3.Трансцендентные звенья.
Для изучения свойств звеньев, в последующем материале установлен следующий порядок рассмотрения их характеристик: переходная характеристика, анализ; частотные характеристики, анализ.
Позиционные звенья. К позиционным звеньям относятся апериодические звенья первого и второго порядков, колебательное и консервативное звено.
Апериодическое звено 1 порядка. К этому типу звеньев относятся устройства, описываемые уравнением
 .
.
Передаточная функция звена 
Колебательное звено. К этому типу звеньев относятся устройства, описываемые уравнением
 .
.
Передаточная функция звена
 .
.
Уравнение (1.48) удобно представить в виде
 x
x  ,
,
где x - параметр затухания колебаний, x =  , ( 0 <
, ( 0 < 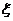 < 1).
< 1).
Если принять  , то колебательное звено становитсяапериодическим второго порядка.
, то колебательное звено становитсяапериодическим второго порядка.
Очевидно, что уравнение звена по внешнему виду совпадает с уравнениями для колебательного звена (1.48) и (1.49). Однако, при 
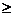 1 характеристическое уравнение звена имеет два вещественных корня (1.52). Поэтому передаточную функцию апериодического звена второго порядка оказывается возможным представить в виде двух последовательно соединенных передаточных функций, рис.1.31.
1 характеристическое уравнение звена имеет два вещественных корня (1.52). Поэтому передаточную функцию апериодического звена второго порядка оказывается возможным представить в виде двух последовательно соединенных передаточных функций, рис.1.31.

Коэффициенты 
Если принять  , то окажется, что
, то окажется, что  и
и  . В этом варианте колебательное звено превращается в консервативное. Уравнение консервативного звена имеет вид
. В этом варианте колебательное звено превращается в консервативное. Уравнение консервативного звена имеет вид
 .
.

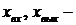 отклонения переменных от своих установившихся значений
отклонения переменных от своих установившихся значений