Тема 3. Теория вероятностей. Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности

1. В урне находятся 3 белых и 3 чёрных шара. Из урны поочерёдно вынимают два шара. Тогда вероятность того, что оба шара белые равна…

-a. ;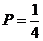

+b. ;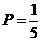

-c. ;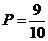

-d. .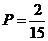

2. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…

-a. Р=0,16;

-b. Р=0,9;

-c. Р=0,3;

+d. Р= 0,2.

3. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…

+a. Р=0,15;

-b. Р=0,8;

-c. Р=0,12;

-d. Р=0,35.

4. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,7 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…

-a. Р=0,4;

-b. Р=0,35;

-c. Р=0,3;

+d. Р=0,28.

5. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,8 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…

-a. Р=0,3;

-b. Р=0,32;

+c. Р=0,24;

-d. Р=0,5.

6. Вероятность того, что при бросании игрального кубика выпадет 1, или 2, или 6 очков, составляет …

+a. Р=0,5;

-b. ;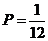

-c. Р=9;

-d. .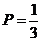

7. В урне находится 5 белых и 2 чёрных шара. Из урны вынимаются четыре шара. Вероятность того, что все шары будут белыми, равна …

-a. ;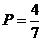

-b. ;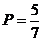

-c. ;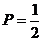

+d. .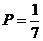

8. В урне находится 5 белых и 3 чёрных шара. Из урны вынимаются четыре шара. Вероятность того, что все шары будут белыми, равна …

-a. ;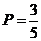

-b. ;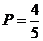

-c. ;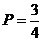

+d. .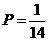

9. В урне находится 5 белых и 3 черных шара. Из урны вынимаются четыре шара. Вероятность того, что два шара будут белыми, а два – черными, равна …

-a. ;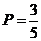

-b. ;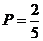

+c. ;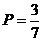

-d. .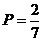

10. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее пяти очков, равна…

-a. ;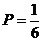

+b. ;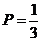

-c. ;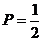

-d. .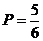

11. На пути движения автомобиля находится 3 светофора. Каждый из них разрешает дальнейшее движение с вероятностью 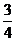и запрещает с вероятностью 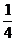. Тогда вероятность того, что хотя бы перед одним светофором автомобиль сделает остановку, равна …

+a. ;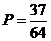

-b. ;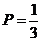

-c. ;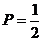

-d. .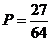

12. Для вероятности 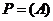любого случайного события выполнено условие

-a. 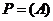>0;

-b. 0< <1;

+c. 0≤ ≤1;

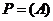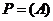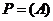-d. <1.

13. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,05. Тогда вероятность банкротства обоих предприятий равна…

+a. Р=0,005;

-b. Р=0,855;

-c. Р=0,05;

-d. Р=0,15.

14. В лотерее 1000 билетов. На один билет выпадает выигрыш 5000 рублей, на десять билетов – выигрыши по 1000 рублей, на пятьдесят билетов – выигрыши по 200 рублей, на сто билетов – выигрыши по 50 рублей; остальные билеты проигрышные. Покупается один билет. Тогда вероятность выигрыша 250 рублей равна …

+a. Р=0;

-b. Р=0,2;

-c. Р=0,15;

-d. Р=1.

15. По мишени производится три выстрела. Значение вероятности ни одного попадания при всех трёх выстрелах равно 0,5; значение вероятности ровно одного попадания - 0,3; значение вероятности ровно двух попаданий – 0,15. Тогда вероятность того, что мишень будет поражена не более одного раза будет равна…

-a. Р=0,15;

-b. Р=0,9;

-c. Р=0,3;

+d. Р=0,8.

16. Идёт борьба между танком и противотанковым орудием. Первым огонь открывает противотанковое орудие и может уничтожить танк с вероятностью 0,5. Если танк не уничтожен, он открывает огонь и может уничтожить орудие с вероятностью 0,7. Найти вероятность того, что орудие будет уничтожено.

-a. ;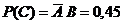

-b. ;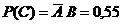

+c. .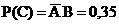

17. Огневой взвод ведёт огонь по оборонительному сооружению. Вероятности попадания в оборонительное сооружение равны: для первого орудия - 0,2, для второго - 0,3, для третьего - 0,4, и от выстрела к выстрелу не изменяются. Начиная с первого, орудия ведут огонь последовательно. Каждое может произвести один выстрел. Какова вероятность вывода оборонительного сооружения из строя, если для этого требуются два попадания? После двух попаданий стрельба прекращается.

-a. Р=0,15;

-b. Р=0,25;

-c. Р=0,32;

+d. Р=0,21.

18. Огневой взвод ведёт огонь по танку. Вероятность попадания в танк равны: для первого орудия - 0,3, для второго - 0,4, для третьего - 0,2. Каждое может произвести только один выстрел. Какова вероятность вывода танка из строя, если для этого требуются два попадания? После двух попаданий стрельба прекращается.

+a. ;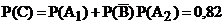

-b. .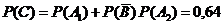

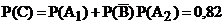
19. Цель состоит из трёх отсеков. Вероятность попадания в каждый из них при заданном положении средней траектории при одном выстреле равна: в первый – 0,2, во второй – 0,3 и в третий – 0,1. Вероятности уничтожения цели при попадании в эти отсеки соответственно равны: 0,2; 0,3; и 0,6. Определить вероятность уничтожения цели.

-a. ;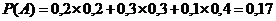

+b. .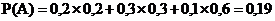

20. Цель состоит из трёх отсеков. Вероятность попадания в каждый из них при заданном положении центра рассеивания снарядов при одном выстреле равна: в первый – 0,1, во второй – 0,2 и в третий – 0,5. Вероятности уничтожения цели при попадании в эти отсеки соответственно равны: 0,5; 0,3; и 0,1. В результате выстрела цель оказалась уничтоженной. В какой из отсеков вероятнее всего произошло попадание.

-a. ;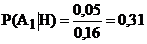

+b. ;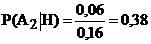

-c. .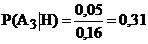

21. Цель состоит из четырёх отсеков, составляющих соответственно 40; 30; 20 и 10% её общей площади. Вероятности поражения цели при попадании в эти отсеки соответственно равны: 0,2; 0,3; 0,4; и 0,5. Определить вероятность поражения цели.

-a. Р=0,1;

-b. Р=0,2;

+c. Р=0,3;

-d. Р=0,4.

22. Цель состоит из двух отсеков, составляющих соответственно 95 и 5% её общей площади. Вероятности поражения цели при попадании в эти отсеки соответственно равны: 0,1; 0,9. В результате попадания цель оказалась поражённой. В какой из отсеков вероятнее всего произошло попадание, если оно равновозможно в любую часть площади цели?

+a. ;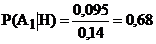

-b. .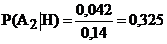

23. Для стрельбы на поражение установки подготовлены таким образом, что центр рассеивания снарядов может быть удален от центра цели в следующих пределах: на величину одной срединной ошибки подготовки — с вероятностью 0,5; от одной до двух — 0,32; от двух до трёх—0,14; от трёх до четырёх—0,04. Вероятность поражения цели при одном выстреле при нахождении центра рассеивания снарядов в пределах: одной срединной ошибки—0,8; от одной до двух—0,3; от двух до трёх—0,1; от трёх до четырёх — 0,01. Определить вероятность поражения цели при одном выстреле.

-a. Р=0,51;

-b. Р=0,28;

-c. Р=0,38;

+d. Р=0,61.

24. Батарея может произвести залп с одной из трёх позиций. Вероятность того, что батарея будет выполнять задачу с первой позиции — 0,4, со второй позиции —0,25; с третьей позиции — 0,35. Вероятность поражения цели при стрельбе с первой позиции равна 0,8, со второй позиции — 0,6, с третьей позиции — 0,4. Определить вероятность поражения цели, если залп будет произведён с одной из позиций.

-a. ;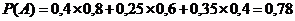

+b. .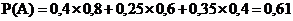

25. Батарея может произвести залп с одной из трёх позиций. Вероятность того, что батарея будет выполнять задачу с первой позиции — 0,4, со второй позиции —0,3; с третьей позиции — 0,3. Вероятность поражения цели при стрельбе с первой позиции равна 0,4, со второй позиции — 0,5, с третьей позиции — 0,4. В результате залпа с одной из огневых позиций цель оказалась поражённой. С какой позиции вероятнее всего был произведён залп.

-a. ;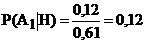

-b. ;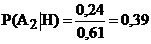

+c. .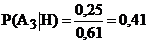

26. При совершении марша колонна может двигаться по одному из трёх маршрутов. Вероятность того, что колонна будет двигаться по маршруту № 1 равна 0,2, по маршруту № 2 - 0,3 и по маршруту № 3 - 0,5. Вероятность поражения колонны при её движении по маршруту № 1 равна 0,2, по маршруту № 2 - 0,4, по маршруту № 3 - 0,5. Какова вероятность поражения колонны?

+a. ;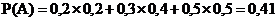

-b. .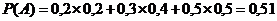

27. При совершении марша колонна может двигаться по одному из трёх маршрутов. Вероятность того, что колонна будет двигаться по маршруту № 1 равна 0,2, по маршруту № 2 - 0,3, по маршруту № 3 - 0,5. Вероятность поражения колонны при её движении по маршруту № 1 равна 0,6, по маршруту № 2 - 0,8, по маршруту № 3 - 0,5. В результате стрельбы колонна оказалась поражённой. По какому из маршрутов вероятнее всего она двигалась?

-a. ;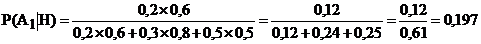

-b. ;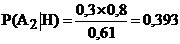

+c. .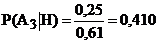

b.