Итогового квалификационного экзамена

Итогового квалификационного экзамена

Для бакалавров

(направление 010200 – Математика. Прикладная математика)

Учебный год

Структура программы:

Программа государственного экзамена по направлению 010200 – Математика. Прикладная математика определяется факультетом на основании методических рекомендаций и соответствующей примерной программы, разработанных НМС по математике и механике УМО университетов, Положения об итоговой государственной аттестации выпускников высших учебных заведений, утвержденного Минобразованием России, и Государственного образовательного стандарта по направлению 010200 – Математика. Прикладная математика.

1. В про­грам­ме пред­став­ле­ны раз­де­лы по блоку общепрофессиональные дисциплины:

ал­геб­ра, ма­те­ма­ти­че­ский ана­лиз, аналитическая геометрия, дифференциальная геометрия, диф­фе­рен­ци­аль­ные урав­не­ния, функциональный анализ, тео­рия функ­ций ком­плекс­но­го пе­ре­мен­но­го, ма­те­ма­ти­че­ская ло­ги­ка и тео­рия ал­го­рит­мов, стохастический анализ.

2. Об­щее ко­ли­че­ст­во во­про­сов про­грам­мы – 36.

3. Ка­ж­дый би­лет со­дер­жит 2 теоретических во­про­са и 1 задачу по теме, входящей в программу итогового квалификационного экзамена.

4. В ка­че­ст­ве во­про­сов фор­му­ли­руются ос­нов­ные тео­ре­ти­че­ские по­ло­же­ния, пред­по­ла­гаю­щие их раз­вер­ну­тое обос­но­ва­ние при от­ве­те.

5. Фор­му­ли­ров­ка ка­ж­до­го во­про­са чет­ко оп­ре­де­ляет рам­ки и объ­ем со­дер­жа­ния от­ве­та.

6. В при­ло­же­нии по ка­ж­до­му разделу ука­зан ре­ко­мен­дуе­мый ис­точ­ник, дос­туп­ный для ис­поль­зо­ва­ния в про­цес­се под­го­тов­ки к эк­за­ме­ну.

Требования к профессиональной подготовленности бакалавра.

Бакалавр математики подготовлен преимущественно к выполнению исследовательской деятельности, в областях, использующих математические методы и компьютерные технологии; созданию и использованию математических моделей процессов и объектов; разработке эффективных математических методов решения задач естествознания, техники, экономики и управления; программно-управленческому обеспечению научно-исследовательской, проектно конструкторской и эксплуатационно-управленческой деятельности.

Бакалавр математики должен знать и уметь использовать:

- основные понятия и методы ал­геб­ры, ма­те­ма­ти­че­ского ана­лиза, аналитической геометрии, дифференциальной геометрии, диф­фе­рен­ци­аль­ных урав­не­ний, функционального анализа, тео­рии функ­ций ком­плекс­но­го пе­ре­мен­но­го, ма­те­ма­ти­че­ской ло­ги­ки и тео­рии ал­го­рит­мов, стохастического анализа;

- математические модели простейших систем и процессов в естествознании и технике;

- вероятностные модели для конкретных процессов и явлений, проводить необходимые расчеты в рамках построенной модели;

- современные методы программирования и методы разработки эффективных алгоритмов решения прикладных задач.

Содержание программы:

Алгебра

1. Понятие группы. Группа ортогональных матриц. Группа комплексных корней 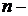ой степени из 1.

2. Деление многочленов с остатком. Алгоритм Евклида. Критерий взаимной простоты двух многочленов.

3. Понятие линейного пространства и его базиса. Линейные преобразования. Собственные значения и собственные векторы линейных преобразований.

4. Фундаментальная система решений системы линейных однородных уравнений. Ядро линейного оператора и его базис.

5. Положительные определенные квадратичные формы. Критерий Сильвестра.

6. Симметрические преобразования евклидовых пространств.

Математический анализ

7. Предел числовой последовательности. Основные свойства: единственность предела; ограниченность сходящейся последовательности; сходимость подпоследовательности сходящейся последовательности. Предел и арифметические операции. Принцип Больцано - Вейерштрасса. Критерий Коши сходимости числовой последовательности. Предел монотонной последовательности.

8. Предел и непрерывность функции. Эквивалентные определения (по Коши и по Гейне). Основные свойства. Связь с арифметическими операциями. Непрерывность композиции. Односторонние пределы и односторонняя непрерывность.

9. Теорема Вейерштрасса об ограниченности и о достижении экстремальных значений функции непрерывной на отрезке. Теорема Коши о промежуточных значениях непрерывной функции. Непрерывность обратной функции.

10. Дифференцируемость числовой функции. Производная и дифференциал. Непрерывность дифференцируемой функции. Геометрический смысл производной. Дифференцируемость и арифметические операции. Дифференцируемость композиции и обратной функции.

11. Теоремы Ферма, Ролля, Коши и Лагранжа о дифференцируемых функциях. Необходимые и достаточные условия экстремума функции в терминах производной.

12. Интеграл Римана. Основные свойства интеграла: линейность, монотонность, аддитивность. Классы функций интегрируемых по Риману. Формула Ньютона-Лейбница. Замена переменной в интеграле Римана и интегрирование по частям в интеграле Римана.

13. Первообразная и неопределенный интеграл. Интеграл с переменным верхним пределом. Теорема о существовании первообразной. Интегрирование по частям и замена переменной в неопределённом интеграле.

14. Числовые ряды. Понятие сходимости числового ряда Необходимое условие сходимости. Признаки сравнения, Коши и Даламбера сходимости положительных рядов. Признак Лейбница сходимости знакопеременного ряда.

15. Функциональные последовательности и ряды. Поточечная и равномерная сходимость. Непрерывность предельной функции равномерно сходящейся функциональной последовательности непрерывных функций и суммы равномерно сходящегося функционального ряда, образованного непрерывными функциями. Предельный переход под знаком интеграла. Почленное интегрирование функционального ряда. Дифференцирование функциональных последовательностей и рядов.

16. Степенные ряды. Теорема Коши - Адамара о структуре области сходимости степенного ряда. Радиус и интервал сходимости. Равномерная сходимость степенных рядов. Теорема Абеля о равномерной сходимости степенного ряда на отрезке, содержащемся в интервале сходимости. Непрерывность суммы степенного ряда. Почленное дифференцирование и интегрирование степенных рядов.

17. Ряды Фурье. Достаточные условия сходимости ряда Фурье. Неравенство Бесселя и равенство Парсеваля для тригонометрических рядов.

Аналитическая геометрия

18. Различные виды уравнения прямой на плоскости и в пространстве. Расстояние от точки до прямой на плоскости. Угол между двумя прямыми.

19. Определение кривых второго порядка, их канонические уравнения. Эксцентриситет, директрисы кривых второго порядка, теорема об эксцентриситете.

Дифференциальные уравнения

24. Обыкновенное дифференциальное уравнение первого порядка. Общее и частное решения дифференциального уравнения. Задача Коши. Теорема о существовании решения задачи Коши для дифференциального уравнения первого порядка.

25. Линейное уравнение n-ого порядка с постоянными коэффициентами. Методы нахождения общего решения.

Функциональный анализ

26. Измеримые множества на прямой. Основные свойства меры Лебега.

27. Интеграл Лебега. Сравнение интегралов Римана и Лебега.

28. Определения и примеры банаховых и гильбертовых пространств.

29. Линейные непрерывные операторы в нормированных пространствах. Эквивалентность ограниченности и непрерывности линейных операторов Норма линейного оператора.

Стохастический анализ

35. Схема независимых испытаний, формулы Бернулли, приближенные формулы для расчета биномиальных вероятностей.

36. Статистические модели, характеристика стандартных параметрических моделей, методы оценки параметров.

Методы оптимизации

37. Постановка задачи оптимального управления. Функция Понтрягина. Принцип

максимума Понтрягина для задач оптимального управления.

38. Синтез оптимального управления. Принцип оптимальности Беллмана.

Методы вычислений

39. Постановка задачи интерполирования функции многочленами. Интерполяционный многочлен Лагранжа. Оценка погрешности интерполирования.

40. Метод последовательных приближений. Достаточное и необходимое и достаточное условия сходимости метода при произвольном начальном приближении.

Программа утверждена на заседании Совета математического факультета № 5 от 3 февраля 20012 г.

Декан математического факультета А.Н.Цирулёв

Приложение к программе

Учебный год

Список литературы для подготовки к экзамену:

Литература к разделу

Ал­геб­ра

1. Кострикин А.И. введение в алгебру М., Наука, 1977.

2. Фаддеев Д.К. Лекции по алгебре. М.. Наука, 1984.

3. Курош А.Г. Курс высшей алгебры. М., Наука, 1975.

4. Проскуряков И.В. Сборник задач по линейной алгебре. М., Наука, 1974.

5. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М,, Наука, 1984.

Литература к разделу

Ма­те­ма­ти­че­ский ана­лиз

1. Ильин В.А., Садовничий В.А., Сендов Б. Х. Математический анализ. М., 1981;

2. Кудрявцев Л.Д. Курс математического анализа. М. 1981;

3. Гусев А.И. Обзорные лекции по математическому анализу. Сервер локальной сети ТвГУ М:\Для студентов А.И. Гусева\ 5 курс.

Литература к разделу

Аналитическая геометрия

1. Александров П.С. Аналитическая геометрия. М.: Наука, 1979.

2. Eфимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1975.

3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1987.

4. Ильин В.А., Поздняк Э.Г. Аналитическая геометрия. М.: Наука, 1988.

5. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 1986.

Литература к разделу

Литература к разделу

Диф­фе­рен­ци­аль­ные урав­не­ния

1. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: Наука, 1970.

2. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1976.

3. Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука, 1976.

4. Федорюк М.В. Обыкновенные дифференциальные уравнения. М.: Наука, 1985.

6. Филлипов А.В. Сборник задач по дифференциальным уравнениям. М., Наука, 1975.

Литература к разделу

Функциональный анализ

1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального

анализа, М., Наука, 1972.

2. Рудин У. Функциональный анализ, М., Мир, 1975

3. Треногин В.А. и др. Задачи и упражнения по функциональному анализу, М., Наука, 1984.

4. Натансон И.П. Теория функций вещественной переменной, М., Наука, 1974

Литература к разделу

Тео­рия функ­ций ком­плекс­но­го пе­ре­мен­но­го

1. Шабат Б.В. Введение в комплексный анализ. Т.1. М., 1969 и другие издания.

2. Привалов И.И. Введение в теорию функций комплексного переменного. М, 1984 и другие издания.

3. Сидоров Ю.В., Федоркж М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. М., 1982 и другие издания.

4. Голубев А.А., Граф С.Ю., Шеретов В.Г. Практический курс комплексного анализа Тверь, 2003.

5. Маркушевич А.Н. Краткий курс теории аналитических функций. М., 1978 и другие издания.

6. Евграфов М.А. Аналитические функции. М, 1991 и другие издания.

7. Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций комплексного переменного. М., 1975.

Литература к разделу

Ма­те­ма­ти­че­ская ло­ги­ка и тео­рия ал­го­рит­мов

1. Мендельсон Э. Введение в математическую логику М., Наука, 1984.
2. Лавров И.А. Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М., Наука, 1984.
3. Яблонский С.В. Введение в дискретную математику. М., Наука, 1979.
4. Гладкий А.В. Конспект лекций по математической логике и теории множеств. Калинин. 1974.
5. Гаврилов Г.П. Сапоженко А.А. Сборник задач по дискретной математике. М., Наука, 1977.

Литература к разделу

Стохастический анализ

1. Гнеденко Б.В. Курс теории вероятностей. М.: Наука,1988.

2. Боровков А.А. Теория вероятностей. М. .: Наука, 1986.

4. Коваленко И.Н., Л.А.Филиппова. Теория вероятностей и математическая статистика. М.: Наука,1982

5. Колемаев В.A. Теория вероятностей и математическая статистика. М.,1991

6. Севастьянов Б.A. Сборник задач по теории вероятностей и математической статистике. М.: Наука,1984.

Литература к разделу

Методы оптимизации

1. Андреева Е.А. Оптимальное управление динамическими системами. Ч. 1, 2. Тверь, 1999.

2. Андреева Е.А., Цирулева В.М. Вариационное исчисление и методы оптимизации, ТвГУ, 2001.

3. Афанасьев В. Н., Колмановский В.Б., Носов В. Р. Математическая теория конструирования систем управления. М.: Высшая школа, 1998.

Литература к разделу

1. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1998.

2. 2.Бахвалов Н.С., Жидков В.П., Кобельков Г.М. Численные методы. М.–С.П.: Физматлит, 2000.

3. Вержбицкий В.М. Численные методы: линейная алгебра и нелинейные уравнения. М.: Высшая школа, 2000.

4. Вержбицкий В.М. Численные методы: математический анализ и обыкновенные дифференциальные уравнения. М.: Высшая школа, 2001

Декан математического факультета А.Н.Цирулёв

итогового квалификационного экзамена

Для бакалавров

(направление 010200 – Математика. Прикладная математика)

Учебный год

Структура программы:

Программа государственного экзамена по направлению 010200 – Математика. Прикладная математика определяется факультетом на основании методических рекомендаций и соответствующей примерной программы, разработанных НМС по математике и механике УМО университетов, Положения об итоговой государственной аттестации выпускников высших учебных заведений, утвержденного Минобразованием России, и Государственного образовательного стандарта по направлению 010200 – Математика. Прикладная математика.

1. В про­грам­ме пред­став­ле­ны раз­де­лы по блоку общепрофессиональные дисциплины:

ал­геб­ра, ма­те­ма­ти­че­ский ана­лиз, аналитическая геометрия, дифференциальная геометрия, диф­фе­рен­ци­аль­ные урав­не­ния, функциональный анализ, тео­рия функ­ций ком­плекс­но­го пе­ре­мен­но­го, ма­те­ма­ти­че­ская ло­ги­ка и тео­рия ал­го­рит­мов, стохастический анализ.

2. Об­щее ко­ли­че­ст­во во­про­сов про­грам­мы – 36.

3. Ка­ж­дый би­лет со­дер­жит 2 теоретических во­про­са и 1 задачу по теме, входящей в программу итогового квалификационного экзамена.

4. В ка­че­ст­ве во­про­сов фор­му­ли­руются ос­нов­ные тео­ре­ти­че­ские по­ло­же­ния, пред­по­ла­гаю­щие их раз­вер­ну­тое обос­но­ва­ние при от­ве­те.

5. Фор­му­ли­ров­ка ка­ж­до­го во­про­са чет­ко оп­ре­де­ляет рам­ки и объ­ем со­дер­жа­ния от­ве­та.

6. В при­ло­же­нии по ка­ж­до­му разделу ука­зан ре­ко­мен­дуе­мый ис­точ­ник, дос­туп­ный для ис­поль­зо­ва­ния в про­цес­се под­го­тов­ки к эк­за­ме­ну.

Требования к профессиональной подготовленности бакалавра.

Бакалавр математики подготовлен преимущественно к выполнению исследовательской деятельности, в областях, использующих математические методы и компьютерные технологии; созданию и использованию математических моделей процессов и объектов; разработке эффективных математических методов решения задач естествознания, техники, экономики и управления; программно-управленческому обеспечению научно-исследовательской, проектно конструкторской и эксплуатационно-управленческой деятельности.

Бакалавр математики должен знать и уметь использовать:

- основные понятия и методы ал­геб­ры, ма­те­ма­ти­че­ского ана­лиза, аналитической геометрии, дифференциальной геометрии, диф­фе­рен­ци­аль­ных урав­не­ний, функционального анализа, тео­рии функ­ций ком­плекс­но­го пе­ре­мен­но­го, ма­те­ма­ти­че­ской ло­ги­ки и тео­рии ал­го­рит­мов, стохастического анализа;

- математические модели простейших систем и процессов в естествознании и технике;

- вероятностные модели для конкретных процессов и явлений, проводить необходимые расчеты в рамках построенной модели;

- современные методы программирования и методы разработки эффективных алгоритмов решения прикладных задач.

Содержание программы:

Алгебра

1. Понятие группы. Группа ортогональных матриц. Группа комплексных корней 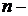ой степени из 1.

2. Деление многочленов с остатком. Алгоритм Евклида. Критерий взаимной простоты двух многочленов.

3. Понятие линейного пространства и его базиса. Линейные преобразования. Собственные значения и собственные векторы линейных преобразований.

4. Фундаментальная система решений системы линейных однородных уравнений. Ядро линейного оператора и его базис.

5. Положительные определенные квадратичные формы. Критерий Сильвестра.

6. Симметрические преобразования евклидовых пространств.

Математический анализ

7. Предел числовой последовательности. Основные свойства: единственность предела; ограниченность сходящейся последовательности; сходимость подпоследовательности сходящейся последовательности. Предел и арифметические операции. Принцип Больцано - Вейерштрасса. Критерий Коши сходимости числовой последовательности. Предел монотонной последовательности.

8. Предел и непрерывность функции. Эквивалентные определения (по Коши и по Гейне). Основные свойства. Связь с арифметическими операциями. Непрерывность композиции. Односторонние пределы и односторонняя непрерывность.

9. Теорема Вейерштрасса об ограниченности и о достижении экстремальных значений функции непрерывной на отрезке. Теорема Коши о промежуточных значениях непрерывной функции. Непрерывность обратной функции.

10. Дифференцируемость числовой функции. Производная и дифференциал. Непрерывность дифференцируемой функции. Геометрический смысл производной. Дифференцируемость и арифметические операции. Дифференцируемость композиции и обратной функции.

11. Теоремы Ферма, Ролля, Коши и Лагранжа о дифференцируемых функциях. Необходимые и достаточные условия экстремума функции в терминах производной.

12. Интеграл Римана. Основные свойства интеграла: линейность, монотонность, аддитивность. Классы функций интегрируемых по Риману. Формула Ньютона-Лейбница. Замена переменной в интеграле Римана и интегрирование по частям в интеграле Римана.

13. Первообразная и неопределенный интеграл. Интеграл с переменным верхним пределом. Теорема о существовании первообразной. Интегрирование по частям и замена переменной в неопределённом интеграле.

14. Числовые ряды. Понятие сходимости числового ряда Необходимое условие сходимости. Признаки сравнения, Коши и Даламбера сходимости положительных рядов. Признак Лейбница сходимости знакопеременного ряда.

15. Функциональные последовательности и ряды. Поточечная и равномерная сходимость. Непрерывность предельной функции равномерно сходящейся функциональной последовательности непрерывных функций и суммы равномерно сходящегося функционального ряда, образованного непрерывными функциями. Предельный переход под знаком интеграла. Почленное интегрирование функционального ряда. Дифференцирование функциональных последовательностей и рядов.

16. Степенные ряды. Теорема Коши - Адамара о структуре области сходимости степенного ряда. Радиус и интервал сходимости. Равномерная сходимость степенных рядов. Теорема Абеля о равномерной сходимости степенного ряда на отрезке, содержащемся в интервале сходимости. Непрерывность суммы степенного ряда. Почленное дифференцирование и интегрирование степенных рядов.

17. Ряды Фурье. Достаточные условия сходимости ряда Фурье. Неравенство Бесселя и равенство Парсеваля для тригонометрических рядов.

Аналитическая геометрия

18. Различные виды уравнения прямой на плоскости и в пространстве. Расстояние от точки до прямой на плоскости. Угол между двумя прямыми.

19. Определение кривых второго порядка, их канонические уравнения. Эксцентриситет, директрисы кривых второго порядка, теорема об эксцентриситете.