Интерпретация множителей Лагранжа

Анализируя значения множителей Лагранжа, можно получить дополнительную ценную информацию. С этим связано широкое распространение метода множителей Лагранжа. Множители Лагранжа измеряют чувствительность оптимального значения 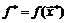к изменениям констант ограничений 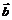. Это следует из утверждений следующей теоремы.

Теорема Лагранжа. Пусть 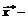решение задачи (3.4)-(3.5), а вектора 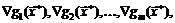определяющие строки матрицы Якоби 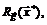являются линейно независимыми. Тогда существует единственный вектор множителей Лагранжа 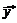, удовлетворяющий вместе с 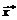системе условий (3.9), причем

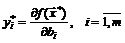. (3.10)

Во многих экономических задачах целевая функция имеет размерность стоимости (цены, умноженной на объем продукции) (прибыль, выручка, издержки), а с помощью ограничений вида (3.5) устанавливаются определенные значения затрат ресурсов. По-сути, в таких задачах множители Лагранжа измеряют чувствительность оптимального значения величины 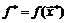, имеющей размерность стоимости, к изменениям некоторого количества затрачиваемых ресурсов. В результате эти множители имеют размерность цены и по этой причине множители Лагранжа часто называют теневыми ценами (данного вида ресурсов).

Пример 3.1.Производственныеиздержки S компании определяются формулой

,

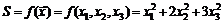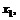
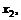
где 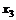– количества (у.е.) расходуемых ресурсов вида 1, 2 и 3 соответственно. Технология производства такова, что требует выполнения следующих условий:

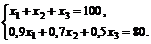
Требуется решить задачу минимизации издержек S и определить значения 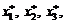обеспечивающие минимальные издержки.

Решение.Исходная задача сводится к следующей ЗНЛП:

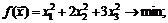
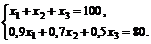
Целевая функция и функции ограничений являются дифференцируемыми, поэтому в данном случае применим метод множителей Лагранжа.

Шаг 1. Вводим вектор множителей Лагранжа .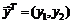

Шаг 2. Определяем функцию Лагранжа

.

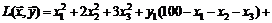
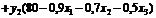Шаг 3. Ищем стационарную точку, решая систему уравнений

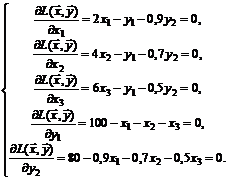
Система имеет единственное решение. Соответствующая стационарная точка, подозрительная на экстремум, есть

.

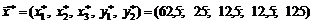Шаг 4. Определяем тип экстремума в стационарной точке. Для этого нужно исследовать окаймленную матрицу Гессе

.

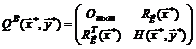Матрица Якоби 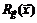в произвольной точке 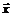имеет вид

.

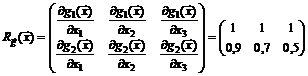Матрица Гессе функции Лагранжа в произвольной точке:

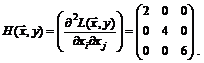
Таким образом, окаймленная матрица Гессе в произвольной, в том числе и в найденной стационарной точке имеет вид:

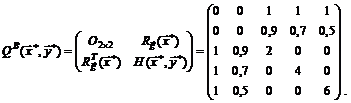
В нашем случае 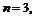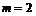. Следовательно, надо проверить 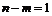главный минор окаймленной матрицы Гессе, начиная с минора порядка 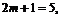то есть определитель полученной окаймленной матрицы Гессе.

Имеем:

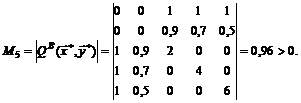
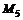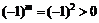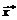Таким образом, знак минора определяются знаком . Следовательно, целевая функция имеет в стационарной точке минимум, причем

.

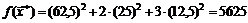Теперь можно сформулировать ответ: компания минимизирует свои издержки при условии использовании ресурсов видов 1, 2 и 3 в количестве 62,5; 25 и 12,5 у.е. соответственно.

Пример 3.2. Функция полезности набора из трех товаров в количестве 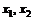и 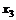единиц соответственно, определяется как

.

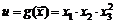Требуется найти стоимость наиболее дешевого набора товаров с заданным значением полезности 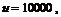если цены товаров равны соответственно 4, 25 и 20 у.е.

Решение. Требуется решить ЗНЛП

.

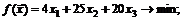
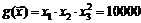Реализуем метод множителей Лагранжа.

Шаг 1. Поскольку имеется всего одно ограничение, то вектор множителей Лагранжа вырождается в скаляр .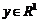

Шаг 2. Определяем функцию Лагранжа

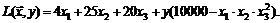
Шаг 3. Ищем стационарную точку, решая систему уравнений

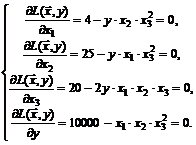(3.11)

Умножая 1-е уравнение (3.11) на 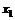, 2-е – на 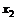, 3-е – на 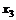, получаем, с учетом 4-го уравнения той же системы, эквивалентную систему уравнений

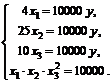(3.12)

Из 1-го и 3-го уравнений (3.12) имеем 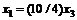; из 2-го и 3-го – 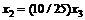. Подстановка этих выражений в 4-е уравнение (3.12) дает 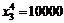, откуда 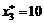и далее простыми подстановками в последние соотношения находим искомые значения компонент единственной стационарной точки:

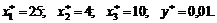
Шаг 4. Для определения типа экстремума функции 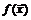в точке 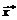нужно исследовать окаймленную матрицу Гессе

.

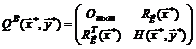Поскольку матрица Якоби 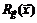в произвольной точке 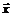есть вектор-строка

,

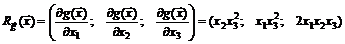то подстановка значений компонент стационарной точки дает

.

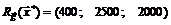Матрица Гессе функции Лагранжа в произвольной точке:

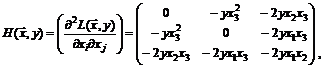
откуда после подстановки значений компонент стационарной точки

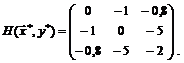
Таким образом, окаймленная матрица Гессе в найденной стационарной точке принимает вид:

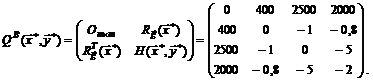
В нашем случае 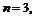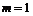. Следовательно, надо проверить 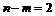главных минора окаймленной матрицы Гессе, начиная с минора порядка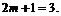

Имеем:

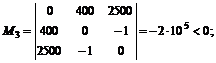
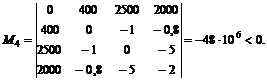
Таким образом, знаки миноров определяются знаком 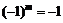. Следовательно, найденная стационарная точка 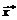определяет набор товаров, обладающий полезностью 1000 и минимальной стоимостью в размере 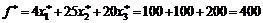у.е. Чувствительность достигнутого значения 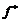к изменению полезности набора товаров при этом равна .

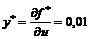Метод подстановки

Метод подстановки применяется для решения ЗНЛП с ограничениями-равенствами:

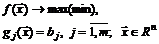
при условии, что система ограничений 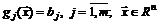этой задачи может быть приведена к виду

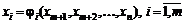. (3.13)

Подстановка выражений (3.13) на место аргументов 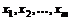в целевой функции 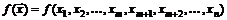дает функцию, зависящую только от :

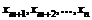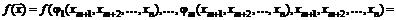
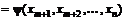. (3.14)

В итоге исходная задача поиска условного экстремума сводится к задаче поиска безусловного экстремума целевой функции 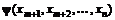. Решая эту задачу классическим методом, находят экстремальные точки 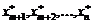, после чего простыми подстановками в (3.13) получают значения m первых переменных исходной задачи: .

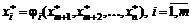Пример 3.3.Получим решение задачи примера 3.1 методом подстановки. Имеем

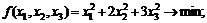
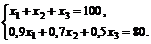
Преобразуя систему уравнений-ограничений, приводим ее к виду

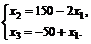
Подстановка полученных выражений для 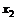и 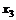в целевую функцию дает

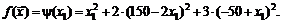
После проведения упрощающих преобразований получаем ЗНЛП без ограничений

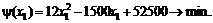
Необходимым условием существования экстремума этой функции одной переменной является условие равенства нулю ее производной в точке экстремума:

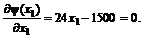
Единственная стационарная точка, являющаяся решением данного уравнения, есть 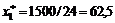. Значение второй производной в стационарной точке больше нуля: 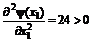, следовательно, эта точка есть точка минимума. Подстановка 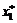в систему ограничений дает

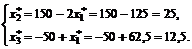
Задачи

Выписать (в произвольной точке) функцию Лагранжа 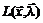, матрицу Якоби 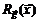вектор-функции 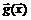ограничений и окаймленную матрицу Гессе 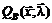для следующих ЗНЛП:

73.

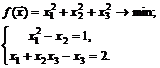
74.

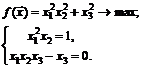
75.

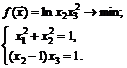
Методом Лагранжа и методом подстановки найти точки условного экстремума следующих функций:

76. 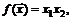если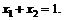

77. 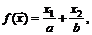если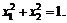

78. 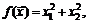если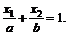

79. 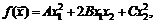если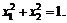

80. 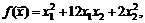если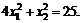

81. 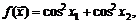если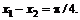

82. 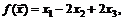если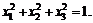

83. 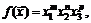если

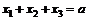
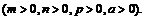
84. 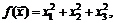если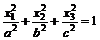

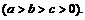
85.

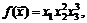
если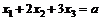

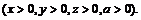
86. 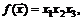если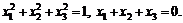

87. 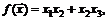если

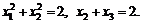
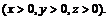
88. 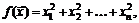если

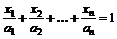
89. 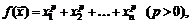если

.

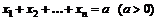90. 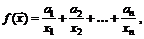если

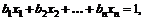
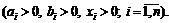
91. 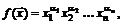если

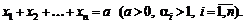
92. Найти экстремум квадратичной формы 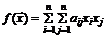при условии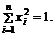

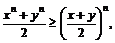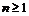93. Доказать неравенство если и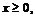

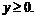
Указание. Искать минимум функции 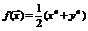при условии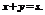

94. Доказать неравенство Гельдера

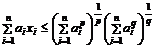
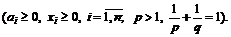
Указание. Искать минимум функции 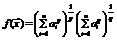при условии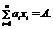

Сформулировать следующие задачи в виде задач нелинейного программирования и решить их:

95. Имеется цемент в количестве 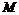; щебень и вода в неограниченном количестве. Требуется построить прямоугольный бассейн наибольшей вместимости. Расход цемента 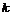на единицу площади дна и стенок бассейна величина постоянная. Найти длину, высоту и глубину нужного бассейна.

96. Имеется цемент в количестве 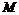; щебень и вода в неограниченном количестве. Требуется построить цилиндрический бассейн наибольшей вместимости. Расход цемента 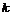на единицу площади дна и стенок бассейна величина постоянная. Найти высоту и диаметр нужного бассейна.

97. Производственная функция определяется как

,

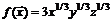где 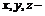значения факторов производства, себестоимости единицы которых равны соответственно, 20, 5 и 10 у.е. Найти максимальное значение выхода готовой продукции при условии, что ее себестоимость будет равна 6000.

98. Гражданин свой совокупный доход в размере 240 руб. тратит на приобретение картофеля и других продуктов питания. Определите оптимальный набор гражданина, если цена картофеля 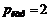руб. за 1 кг, а стоимость условной единицы других благ – 6 руб. за единицу. Функция полезности гражданина имеет вид

1) 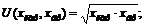2)

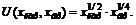
99. Оптимальный набор потребителя составляет 6 ед. блага 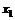и 8 ед. блага 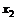. Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. функция полезности потребителя имеет вид:

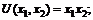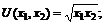1) 2) 3)

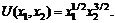
100. Рациональный потребитель из всех имеющихся вариантов выбрал набор, состоящий из 20 ед. блага 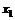и 25 ед. блага 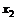. Функция полезности индивида имеет вид: 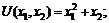располагаемый доход равен 100 руб. в месяц. Определите, как изменится доход потребителя, если новый набор содержит 10 ед. блага 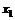и 15 ед. блага 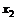, уровень цен не менялся.

101. Консервные банки, изготовляемые из жести, имеют цилиндрическую форму. Радиус основания цилиндра банки равен R см, высота банки – H см. Определить, при каких значениях R и H расход жести на изготовление консервных банок емкостью в 1 литр будет

наименьшим.

102. Производственная функция 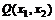фирмы (производственная функция выражает объем выпускаемой фирмой продукции) имеет следующий вид:

,

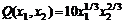где 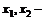затраты ресурсов. Цена покупки фирмой единицы ресурсов 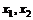равна 5 и 10 у.е. соответственно. Каков наибольший выпуск при общих издержках ?

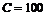103. Производственная функция 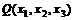фирмы имеет следующий вид:

,

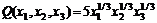где 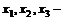затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск затраты ресурсов при условии, что .

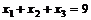104. Производственная функция 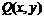фирмы описывается функцией Кобба-Дугласа:

,

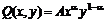где А=0,75 – технологический коэффициент, x– затраты капитала, y – суммарные затраты ресурсов. Найти значения величин x и y при ценах используемых ресурсов соответственно 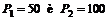, чтобы при фиксированном объеме выпускаемой продукции 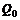обеспечивался минимум затрат 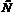, выражаемых формулой

.

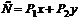При поиске решения принять ;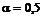

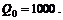
4.РЕШЕНИЕ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ОГРАНИЧЕНИЯХ-НЕРАВЕНСТВАХ

Рассматривается ЗНЛП вида

(4.1)

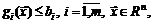(4.2)

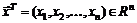где – целевая функция; – вектор неизвестных; 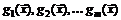– функции ограничений. В векторной форме записи эта задача принимает вид

(4.3)

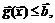(4.4)

где 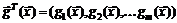– m-мерная вектор-функция ограничений.