Нелинейного программирования
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
В.И. Рюмкин
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Томск
УДК 519.6
Рюмкин В.И.Методы решения задач нелинейного программирования: Учебное пособие. – Томск: ТГУ, 2006. – 56 с.
В учебном пособии рассматриваются методы решения задач нелинейного программирования. Приведены примеры практических задач экономики, формальные математические постановки которых является задачами нелинейного программирования. Рассмотрены основные методы решения таких задач. Представлены примеры задач для самостоятельной работы.
Учебное пособие разработано для студентов экономического факультета дневной и вечерней форм обучения ТГУ и студентов Высшей школы бизнеса ТГУ.
УДК 519.6
Рецензент – профессор С.Н. Колупаева
© Рюмкин В.И.
ВВЕДЕНИЕ
Задачи прикладной математики имеют дело с математическими моделями объектов или процессов.Математической моделью называются формальные математические соотношения, устанавливающие связь принятого критерия эффективности с действующими факторами модели. Решением задачи, связанной с выбранной математической моделью, называется конкретный набор значений контролируемых параметров. Задачей математического программирования, или оптимизационной задачей, называется задача, состоящая в определении оптимального решения, которое в рамках принятой математической модели задает экстремальные значения критерию эффективности.
Критерий эффективности выражается некоторой функцией 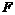 , называемой целевой, аргументами которой являются как действующие факторы
, называемой целевой, аргументами которой являются как действующие факторы 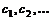 , так и элементы решения
, так и элементы решения 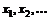 :
:
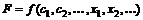 .
.
Тогда задача математического программирования может быть представлена в следующей записи:
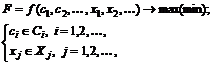 (*)
(*)
где множества 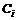 и
и 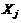 задаются равенствами и неравенствами и представляют собой множества допустимых значений действующих факторов и элементов решений. В зависимости от вида целевой функции, а также особенностей множеств
задаются равенствами и неравенствами и представляют собой множества допустимых значений действующих факторов и элементов решений. В зависимости от вида целевой функции, а также особенностей множеств 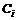 и
и 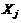 , задача (*) принимает различные постановки, каждая из которых требуют применения подходящих методов решения.
, задача (*) принимает различные постановки, каждая из которых требуют применения подходящих методов решения.
В данном пособии рассматриваются методы решения задач нелинейного программирования. К задачам такого класса относится задача (*), если либо целевая функция 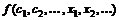 не является линейной[1], либо множества допустимых значений
не является линейной[1], либо множества допустимых значений 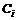 и
и 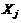 задаются нелинейными равенствами и неравенствами, либо то и другое вместе.
задаются нелинейными равенствами и неравенствами, либо то и другое вместе.
Разновидности ЗМП
Приведем в порядке возрастания сложности решения несколько классов ЗМП.
а) ЗМП при отсутствии ограничений.
 . (1.3)
. (1.3)
Для задач этого класса допустимое множество совпадает со всем векторным пространством ( 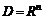 ). Решением может служить любая точка
). Решением может служить любая точка 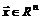 (ограничений нет).
(ограничений нет).
б) ЗМП с ограничениями-равенствами:
 (1.4)
(1.4)
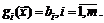 (1.5)
(1.5)
Для задач этого класса допустимое множество определяется как множество решений системы уравнений:
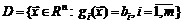 .
.
в) ЗМП с ограничениями-неравенствами:
 (1.6)
(1.6)
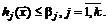 (1.7)
(1.7)
Для задач этого класса допустимое множество определяется как множество решений системы неравенств:
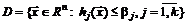 .
.
г) ЗМП со смешанными ограничениями (ограничениями смешанного типа):
 (1.8)
(1.8)
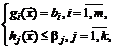 (1.9)
(1.9)
когда система ограничений представляется совокупностью уравнений и неравенств:
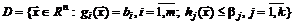 .
.
Функция 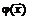 называется линейной функцией, если она может быть представлена в виде
называется линейной функцией, если она может быть представлена в виде 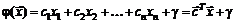 , где
, где 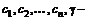 заданные числовые константы. В противном случае функция
заданные числовые константы. В противном случае функция 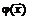 называется нелинейной.
называется нелинейной.
ЗМП называется задачей линейного программирования (ЗЛП), если целевая функции  является линейной функцией, а область ограничений
является линейной функцией, а область ограничений 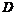 представляет собой выпуклый многогранник. В противном случае ЗМП называется задачей нелинейного программирования (ЗНЛП).
представляет собой выпуклый многогранник. В противном случае ЗМП называется задачей нелинейного программирования (ЗНЛП).
Функции ограничений 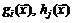 , определяющие допустимое множество ЗМП, в общем случае являются нелинейными функциями. Если же целевая функция и функции ограничений являются линейными, то тогда ЗМП классов б), в), г) оказываются задачами линейного программирования в канонической, симметричной и общей формах представления соответственно.
, определяющие допустимое множество ЗМП, в общем случае являются нелинейными функциями. Если же целевая функция и функции ограничений являются линейными, то тогда ЗМП классов б), в), г) оказываются задачами линейного программирования в канонической, симметричной и общей формах представления соответственно.
Разложение Тейлора
Пусть 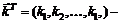 вектор с целочисленными неотрицательными компонентами. Обозначим через
вектор с целочисленными неотрицательными компонентами. Обозначим через 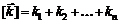 сумму его компонент. Говорят, что функция
сумму его компонент. Говорят, что функция 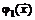 есть «о малое» по сравнению с
есть «о малое» по сравнению с 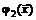 при
при 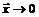 (пишут
(пишут 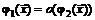 , если справедливо условие
, если справедливо условие
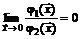 . (1.19)
. (1.19)
Условие (1.19) означает, что 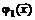 пренебрежимо мала по сравнению с
пренебрежимо мала по сравнению с 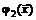 при
при 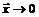 . Если функция
. Если функция 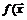 ) дифференцируема
) дифференцируема 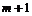 раз в некоторой окрестности
раз в некоторой окрестности 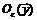 точки
точки 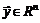 , то для всякой точки
, то для всякой точки 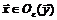 справедлива формула Тейлора
справедлива формула Тейлора
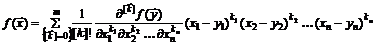 +
+
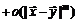 . (1.20)
. (1.20)
Величина 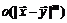 называется остаточным членом в форме Пеано иозначает пренебрежимо малую величину по сравнению с
называется остаточным членом в форме Пеано иозначает пренебрежимо малую величину по сравнению с 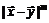 при
при 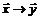 .
.
Представление функции  по формуле Тейлора (1.20) называется разложением Тейлора этой функции в точке
по формуле Тейлора (1.20) называется разложением Тейлора этой функции в точке 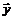 с точностью до производных m-го порядка.
с точностью до производных m-го порядка.
В частности, разложение Тейлора с точностью до производных второго порядка есть
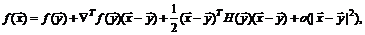 (1.21)
(1.21)
где 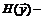 матрица Гессе функции
матрица Гессе функции  в точке
в точке 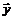 .
.
В одномерном случае, когда 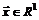 и функция
и функция  является функцией одной переменной, формула Тейлора принимает вид
является функцией одной переменной, формула Тейлора принимает вид
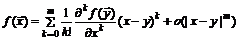 (1.22)
(1.22)
Если функция  является аналитической функцией, то есть дифференцируемой в точке
является аналитической функцией, то есть дифференцируемой в точке 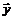 бесконечное число раз, то она может быть разложена в степенной ряд (ряд Тейлора):
бесконечное число раз, то она может быть разложена в степенной ряд (ряд Тейлора):
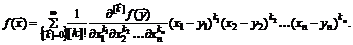 (1.23)
(1.23)
В одномерном случае, когда 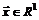 , из (1.22) и (1.23) следует
, из (1.22) и (1.23) следует
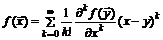 (1.24)
(1.24)
Пример 1.6. Из (1.24) следует, в частности,
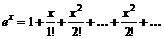 ;
; 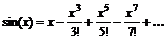
Задачи
Для указанных ниже функций найти все частные производные первого и второго порядка:
1. 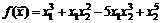 . 2.
. 2. 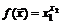 .
.
3. 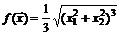 . 4.
. 4. 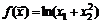 .
.
5. 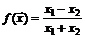 . 6.
. 6. 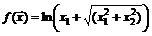 .
.
Для указанных ниже матриц определить, используя критерий Сильвестра, являются ли они положительно или отрицательно определенными:
7. 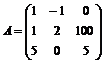 . 8.
. 8. 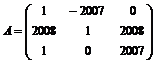 .
.
9. 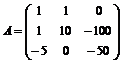 . 10.
. 10. 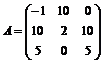 .
.
11. 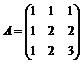 . 12.
. 12.  .
.
Для указанных ниже функций определить, являются ли они выпуклыми или вогнутыми:
13.  . 14.
. 14. 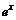 . 15.
. 15. 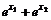 16.
16. 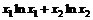
17. 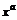 , если
, если 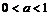 . 18.
. 18. 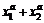 , если
, если 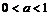 .
.
19. 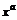 , если
, если 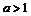 . 20.
. 20. 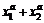 , если
, если 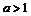 .
.
21. 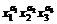 , если
, если 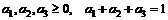 .
.
22. Найти производную функции 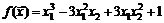 в точке
в точке 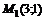 по направлению к точке
по направлению к точке 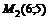 .
.
23. Найти производную функции 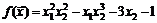 в точке
в точке 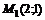 по направлению к началу координат.
по направлению к началу координат.
24.Найти производную функции 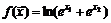 в начале координат в направлении луча, образующего угол
в начале координат в направлении луча, образующего угол 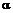 с осью
с осью 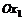 .
.
25. Найти производную функции 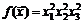 в точке
в точке 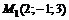 по направлению к точке
по направлению к точке 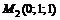 .
.
Для указанных ниже функций найти их стационарные точки:
26. 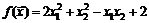 . 27.
. 27. 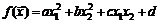 .
.
28. 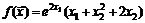 . 29.
. 29. 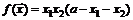 .
.
30. 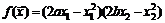 . 31.
. 31. 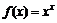 .
.
32. 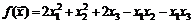 .
.
33. 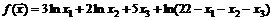 .
.
Найти градиент 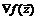 и матрицу Гессе
и матрицу Гессе 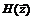 следующих функций:
следующих функций:
34. 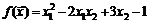 в точке
в точке 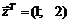 .
.
35. 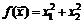 в точке
в точке 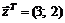 .
.
36. 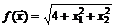 в точке
в точке 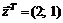 .
.
37. 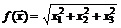 в точке
в точке 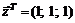 .
.
38. 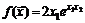 в точке
в точке 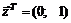 .
.
Разложить по формуле Тейлора следующие функции в заданной точке с точностью до производных второго порядка:
39. 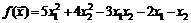 в точке
в точке 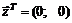 .
.
40. 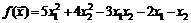 в точке
в точке 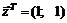 .
.
41. 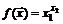 в точке
в точке 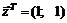 .
.
42. 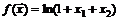 в точке
в точке 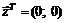 .
.
43. 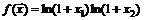 в точке
в точке 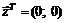 .
.
44. Найти матрицу Якоби 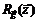 вектор-функции
вектор-функции 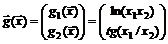 в точке
в точке 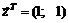 .
.
45. Найти матрицу Якоби 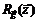 вектор-функции
вектор-функции 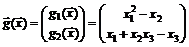 в точке
в точке 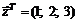 .
.
46. Найти матрицу Якоби 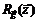 вектор-функции
вектор-функции 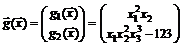 в точке
в точке 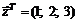 .
.
47. Найти вектор нормали 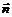 к гиперплоскости, задаваемой уравнением
к гиперплоскости, задаваемой уравнением 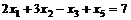 .
.
48. Найти вектор нормали 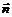 к гиперплоскости, задаваемой уравнением
к гиперплоскости, задаваемой уравнением 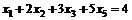 .
.
Задачи
Классическим методом исследовать на экстремум следующие функции и найти (если они есть) все их экстремальные точки:
49. 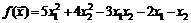 . 50.
. 50. 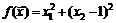 .
.
51. 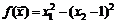 . 52.
. 52. 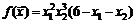 .
.
53. 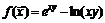 . 54.
. 54. 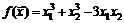 .
.
55. 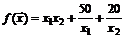 ,
, 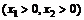 .
.
56. 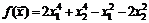 . 57.
. 57.  .
.
58. 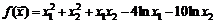 .
.
59. 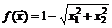 .
.
60. Прибыль P фирмы определяется функцией
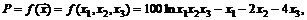
где 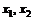 и
и 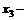 значения факторов производства. Определить максимальную прибыль, а также значения факторов производства, обеспечивающие этот максимум.
значения факторов производства. Определить максимальную прибыль, а также значения факторов производства, обеспечивающие этот максимум.
61. Прибыль P некоторой фирмы определяется функцией
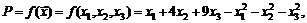
где 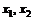 и
и 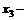 значения факторов производства. Определить максимальную прибыль, а также значения факторов производства, обеспечивающие этот максимум.
значения факторов производства. Определить максимальную прибыль, а также значения факторов производства, обеспечивающие этот максимум.
61. Издержки 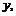 приходящиеся на единицу выпускаемой продукции, выражается функцией:
приходящиеся на единицу выпускаемой продукции, выражается функцией:
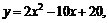
где 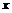 – количество (объем выпуска) этой продукции. При каком объеме выпуска суммарные издержки будут минимальными?
– количество (объем выпуска) этой продукции. При каком объеме выпуска суммарные издержки будут минимальными?
62. Определите оптимальный для потребителя объем блага 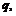 если известно, что функция полезности индивида от обладания этим благом имеет вид:
если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) 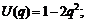 2)
2) 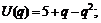 3)
3) 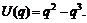
63. Краткосрочные общие затраты (издержки) ТС конкурентной фирмы описываются формулой 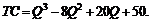 При каком уровне рыночной цены
При каком уровне рыночной цены 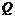 эти издержки будут минимальными?
эти издержки будут минимальными?
64. Автомобиль расходует
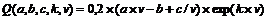
бензина на 100 км пути, где 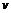 – скорость автомобиля (км/час);
– скорость автомобиля (км/час); 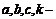 заданные коэффициенты, зависящие от его ходовых свойств. Определить крейсерские[2] скорости автомобилей приведенных в таблице марок.
заданные коэффициенты, зависящие от его ходовых свойств. Определить крейсерские[2] скорости автомобилей приведенных в таблице марок.
| Марка автомобиля | Значения ходовых коэффициентов | |||
| a | b | c | k | |
| ГАЗ 31010 | 0,142 | 0,0052 | ||
| BMW | 0,112 | 0,0042 | ||
| Volvo | 0,121 | 0,0047 |
65. Две деревни А и В расположены на берегу реки на расстоянии 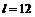 кмдруг от друга, третья деревня С находится на той же стороне реки и удалена от деревень А, В на расстояния соответственно
кмдруг от друга, третья деревня С находится на той же стороне реки и удалена от деревень А, В на расстояния соответственно 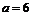 и
и 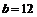 км. Русло реки в окрестностях деревень прямолинейно. В каком месте следует построить пристань, чтобы сумма расстояний от пристани до деревень была бы наименьшей?
км. Русло реки в окрестностях деревень прямолинейно. В каком месте следует построить пристань, чтобы сумма расстояний от пристани до деревень была бы наименьшей?
66. В городе должен быть построен депозитарий крови. Потребителями крови являются три госпиталя, расположенные в точках с координатами, указанными в таблице:
| Госпитали | Расстояние от базовой точки (км) | |
| На восток | На север | |
| Госпиталь №1 | ||
| Госпиталь №2 | ||
| Госпиталь №3 |
Частота обращений за кровью для всех госпиталей одинакова. Определить точку расположения депозитария из критерия минимизации суммарной длины пути по доставке крови в госпитали города.
67. Добываемая в карьере руда автотранспортом поставляется на металлургический комбинат. В 30 км от карьера проходит железная дорога, ведущая (по прямой) на металлургический комбинат. Стоимость перевозки 1 т. руды на 1 км для автотранспорта 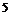 руб., для железнодорожного транспорта 2 руб. В каком месте на железной дороге следует построить станцию для перегрузки руды и отправки далее на комбинат по железной дороге? Расстояние от ближайшей к карьеру точки железной дороги до комбината равно 300 км.
руб., для железнодорожного транспорта 2 руб. В каком месте на железной дороге следует построить станцию для перегрузки руды и отправки далее на комбинат по железной дороге? Расстояние от ближайшей к карьеру точки железной дороги до комбината равно 300 км.
68. Берега некоторого морского пролива описывается параболой 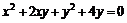 и прямой
и прямой 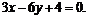 Определить координаты точек на берегах, для которых мост, связывающий эти точки, будет иметь наименьшую длину. Какова будет длина такого моста?
Определить координаты точек на берегах, для которых мост, связывающий эти точки, будет иметь наименьшую длину. Какова будет длина такого моста?
69. Автомобильная горная дорога между пунктами А и В описывает траекторию 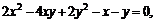 а другая дорога между пунктами С и D проходит по прямой
а другая дорога между пунктами С и D проходит по прямой 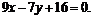 Требуется построить связывающий указанные дороги путепровод, по возможности наиболее короткий. Таким образом, задача состоит в определении точек на дорогах, для которых отрезок, связывающий эти две точки, имеет наименьшую длину.
Требуется построить связывающий указанные дороги путепровод, по возможности наиболее короткий. Таким образом, задача состоит в определении точек на дорогах, для которых отрезок, связывающий эти две точки, имеет наименьшую длину.
70. Морская береговая линия описывается кривой  а судоходный канал проходит по прямой
а судоходный канал проходит по прямой 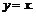 Определить кратчайшее расстояние между морем и каналом, а также координаты точки на морском берегу и на канале, определяющие это кратчайшее расстояние.
Определить кратчайшее расстояние между морем и каналом, а также координаты точки на морском берегу и на канале, определяющие это кратчайшее расстояние.
71. Расходы топлива теплоходом пропорциональны кубу его скорости. Известно, что при скорости в 10 км/ч расходы на топливо составляют 30 руб. в час, остальные же расходы (не зависящие от скорости) составляют 480 руб. в час. При какой скорости парохода общая сумма расходов на 1 км пути будет наименьшей? Какова будет при этом общая сумма расходов в час?
72. Функция выручки фирмы квадратично зависит от объема продукции 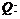
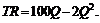
Функция издержек имеет кубическую зависимость от 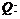
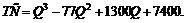
Определить максимальную прибыль фирмы, а также объем выпуска продукции, обеспечивающий эту прибыль.
3. РЕШЕНИЕ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ОГРАНИЧЕНИЯХ-РАВЕНСТВАХ
В данном разделе рассматривается оптимизационная ЗНЛП вида
 (3.1)
(3.1)
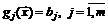 ;
; 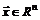 , (3.2)
, (3.2)
которая в более компактной векторной форме записи имеет вид
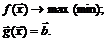 (3.3)
(3.3)
Здесь:  – целевая функция;
– целевая функция; 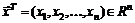 – ее векторный аргумент (вектор неизвестных);
– ее векторный аргумент (вектор неизвестных); 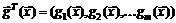 – вектор-функция ограничений;
– вектор-функция ограничений; 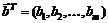 – заданный вектор правой части ограничений.
– заданный вектор правой части ограничений.
Метод множителей Лагранжа
3.1.1. Назначение и обоснование метода
Метод множителей Лагранжа предназначен для решения ЗНЛП типа (3.1)-(3.2), которая в развернутой форме записи имеет вид
 (3.4)
(3.4)
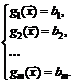 (3.5)
(3.5)
Для безусловного экстремума, когда ограничений нет, и экстремум ищется на всем пространстве, необходимым условием существования экстремума является условие 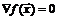 . В случае одного условия область ограничений состоит из поверхности
. В случае одного условия область ограничений состоит из поверхности 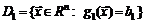 ; градиент
; градиент 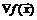 целевой функции в точке экстремума
целевой функции в точке экстремума 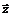 должен быть ортогонален к этой поверхности. В противном случае в касательной плоскости существует направление, вдоль которого производная от функции
должен быть ортогонален к этой поверхности. В противном случае в касательной плоскости существует направление, вдоль которого производная от функции  отлична от нуля (тогда и производная вдоль кривой на поверхности, касающейся этого направления, отлична от нуля). Поэтому, вследствие ортогональности градиента
отлична от нуля (тогда и производная вдоль кривой на поверхности, касающейся этого направления, отлична от нуля). Поэтому, вследствие ортогональности градиента 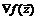 в точке экстремума к поверхности
в точке экстремума к поверхности 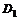 , при некотором
, при некотором 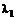 должно выполняться
должно выполняться
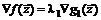 ,
,
иначе говоря, при некотором 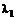
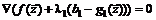 .
.
В случае нескольких ограничений в виде системы уравнений, когда допустимое множество представляет собой поверхность
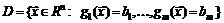 ,
,
градиент должен лежать в нормальной плоскости к поверхности, то есть в плоскости, «натянутой» на векторы
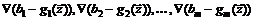 .
.
Следовательно, при некоторых 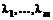 Имеем,
Имеем,
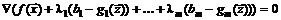 ,
,
то есть
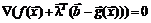 ,
,
что является необходимым условием существования экстремума.
Это условие и ложится в основу метода множителей Лагранжа.
Метод подстановки
Метод подстановки применяется для решения ЗНЛП с ограничениями-равенствами:
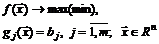
при условии, что система ограничений 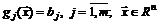 этой задачи может быть приведена к виду
этой задачи может быть приведена к виду
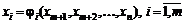 . (3.13)
. (3.13)
Подстановка выражений (3.13) на место аргументов 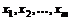 в целевой функции
в целевой функции 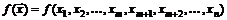 дает функцию, зависящую только от
дает функцию, зависящую только от 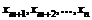 :
:
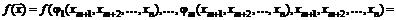
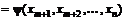 . (3.14)
. (3.14)
В итоге исходная задача поиска условного экстремума сводится к задаче поиска безусловного экстремума целевой функции 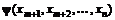 . Решая эту задачу классическим методом, находят экстремальные точки
. Решая эту задачу классическим методом, находят экстремальные точки 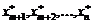 , после чего простыми подстановками в (3.13) получают значения m первых переменных исходной задачи:
, после чего простыми подстановками в (3.13) получают значения m первых переменных исходной задачи: 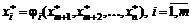 .
.
Пример 3.3.Получим решение задачи примера 3.1 методом подстановки. Имеем
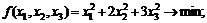
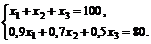
Преобразуя систему уравнений-ограничений, приводим ее к виду
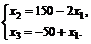
Подстановка полученных выражений для 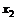 и
и 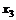 в целевую функцию дает
в целевую функцию дает
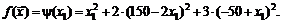
После проведения упрощающих преобразований получаем ЗНЛП без ограничений
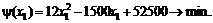
Необходимым условием существования экстремума этой функции одной переменной является условие равенства нулю ее производной в точке экстремума:
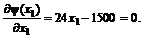
Единственная стационарная точка, являющаяся решением данного уравнения, есть 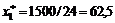 . Значение второй производной в стационарной точке больше нуля:
. Значение второй производной в стационарной точке больше нуля: 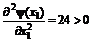 , следовательно, эта точка есть точка минимума. Подстановка
, следовательно, эта точка есть точка минимума. Подстановка 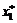 в систему ограничений дает
в систему ограничений дает
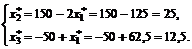
Задачи
Выписать (в произвольной точке) функцию Лагранжа 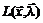 , матрицу Якоби
, матрицу Якоби 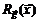 вектор-функции
вектор-функции 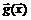 ограничений и окаймленную матрицу Гессе
ограничений и окаймленную матрицу Гессе 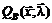 для следующих ЗНЛП:
для следующих ЗНЛП:
73. 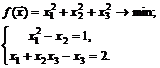
74. 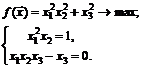
75. 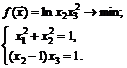
Методом Лагранжа и методом подстановки найти точки условного экстремума следующих функций:
76. 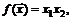 если
если 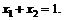
77. 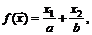 если
если 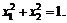
78. 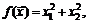 если
если 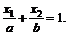
79. 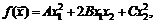 если
если 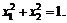
80. 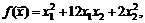 если
если 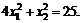
81. 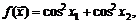 если
если 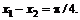
82. 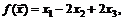 если
если 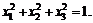
83. 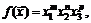 если
если
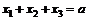
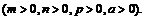
84. 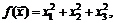 если
если 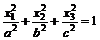
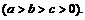
85. 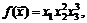
если 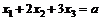
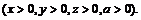
86. 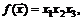 если
если 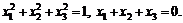
87. 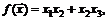 если
если
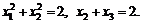
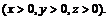
88. 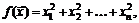 если
если
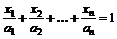
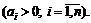
89. 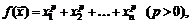 если
если
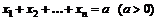 .
.
90. 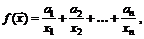 если
если
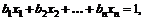
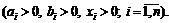
91. 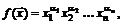 если
если
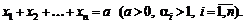
92. Найти экстремум квадратичной формы 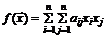 при условии
при условии 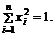
93. Доказать неравенство 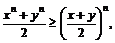 если
если 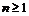 и
и 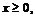
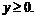
Указание. Искать минимум функции 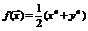 при условии
при условии 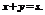
94. Доказать неравенство Гельдера
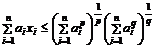
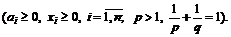
Указание. Искать минимум функции 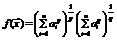 при условии
при условии 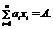
Сформулировать следующие задачи в виде задач нелинейного программирования и решить их:
95. Имеется цемент в количестве 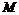 ; щебень и вода в неограниченном количестве. Требуется построить прямоугольный бассейн наибольшей вместимости. Расход цемента
; щебень и вода в неограниченном количестве. Требуется построить прямоугольный бассейн наибольшей вместимости. Расход цемента 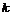 на единицу площади дна и стенок бассейна величина постоянная. Найти длину, высоту и глубину нужного бассейна.
на единицу площади дна и стенок бассейна величина постоянная. Найти длину, высоту и глубину нужного бассейна.
96. Имеется цемент в количестве 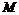 ; щебень и вода в неограниченном количестве. Требуется построить цилиндрический бассейн наибольшей вместимости. Расход цемента
; щебень и вода в неограниченном количестве. Требуется построить цилиндрический бассейн наибольшей вместимости. Расход цемента 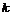 на единицу площади дна и стенок бассейна величина постоянная. Найти высоту и диаметр нужного бассейна.
на единицу площади дна и стенок бассейна величина постоянная. Найти высоту и диаметр нужного бассейна.
97. Производственная функция определяется как
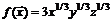 ,
,
где 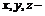 значения факторов производства, себестоимости единицы которых равны соответственно, 20, 5 и 10 у.е. Найти максимальное значение выхода готовой продукции при условии, что ее себестоимость будет равна 6000.
значения факторов производства, себестоимости единицы которых равны соответственно, 20, 5 и 10 у.е. Найти максимальное значение выхода готовой продукции при условии, что ее себестоимость будет равна 6000.
98. Гражданин свой совокупный доход в размере 240 руб. тратит на приобретение картофеля и других продуктов питания. Определите оптимальный набор гражданина, если цена картофеля 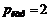 руб. за 1 кг, а стоимость условной единицы других благ – 6 руб. за единицу. Функция полезности гражданина имеет вид
руб. за 1 кг, а стоимость условной единицы других благ – 6 руб. за единицу. Функция полезности гражданина имеет вид
1) 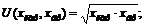 2)
2) 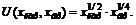
99. Оптимальный набор потребителя составляет 6 ед. блага 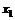 и 8 ед. блага
и 8 ед. блага 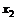 . Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. функция полезности потребителя имеет вид:
. Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. функция полезности потребителя имеет вид:
1) 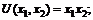 2)
2) 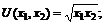 3)
3) 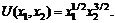
100. Рациональный потребитель из всех имеющихся вариантов выбрал набор, состоящий из 20 ед. блага 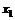 и 25 ед. блага
и 25 ед. блага 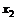 . Функция полезности индивида имеет вид:
. Функция полезности индивида имеет вид: 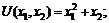 располагаемый доход равен 100 руб. в месяц. Определите, как изменится доход потребителя, если новый набор содержит 10 ед. блага
располагаемый доход равен 100 руб. в месяц. Определите, как изменится доход потребителя, если новый набор содержит 10 ед. блага 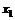 и 15 ед. блага
и 15 ед. блага 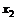 , уровень цен не менялся.
, уровень цен не менялся.
101. Консервные банки, изготовляемые из жести, имеют цилиндрическую форму. Радиус основания цилиндра банки равен R см, высота банки – H см. Определить, при каких значениях R и H расход жести на изготовление консервных банок емкостью в 1 литр будет
наименьшим.
102. Производственная функция 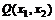 фирмы (производственная функция выражает объем выпускаемой фирмой продукции) имеет следующий вид:
фирмы (производственная функция выражает объем выпускаемой фирмой продукции) имеет следующий вид:
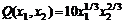 ,
,
где 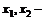 затраты ресурсов. Цена покупки фирмой единицы ресурсов
затраты ресурсов. Цена покупки фирмой единицы ресурсов 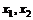 равна 5 и 10 у.е. соответственно. Каков наибольший выпуск при общих издержках
равна 5 и 10 у.е. соответственно. Каков наибольший выпуск при общих издержках 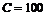 ?
?
103. Производственная функция 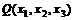 фирмы имеет следующий вид:
фирмы имеет следующий вид:
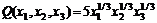 ,
,
где 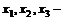 затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск затраты ресурсов при условии, что
затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск затраты ресурсов при условии, что 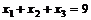 .
.
104. Производственная функция 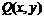 фирмы описывается функцией Кобба-Дугласа:
фирмы описывается функцией Кобба-Дугласа:
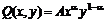 ,
,
где А=0,75 – технологический коэффициент, x– затраты капитала, y – суммарные затраты ресурсов. Найти значения величин x и y при ценах используемых ресурсов соответственно 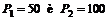 , чтобы при фиксированном объеме выпускаемой продукции
, чтобы при фиксированном объеме выпускаемой продукции 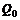 обеспечивался минимум затрат
обеспечивался минимум затрат 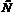 , выражаемых формулой
, выражаемых формулой
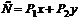 .
.
При поиске решения принять 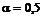 ;
; 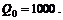
4.РЕШЕНИЕ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ОГРАНИЧЕНИЯХ-НЕРАВЕНСТВАХ
Рассматривается ЗНЛП вида
 (4.1)
(4.1)
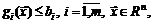 (4.2)
(4.2)
где  – целевая функция;
– целевая функция; 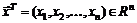 – вектор неизвестных;
– вектор неизвестных; 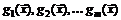 – функции ограничений. В векторной форме записи эта задача принимает вид
– функции ограничений. В векторной форме записи эта задача принимает вид
 (4.3)
(4.3)
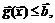 (4.4)
(4.4)
где 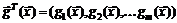 – m-мерная вектор-ф
– m-мерная вектор-ф
