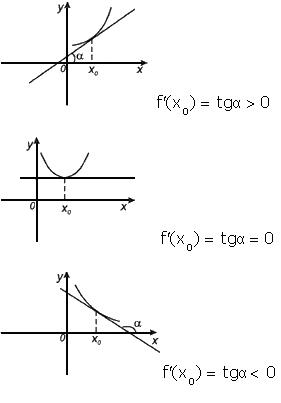С помощью матрицы алгебраических дополнений

Умножение матрицы на число

Умножение матрицы 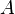на число (обозначение: ) заключается в построении матрицы , элементы которой получены путём умножения каждого элемента матрицы 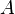на это число, то есть каждый элемент матрицы равен

Свойства умножения матриц на число:

• 1. 1A = A;

• 2. (λβ)A = λ(βA)

• 3. (λ+β)A = λA + βA

• 4. λ(A+B) = λA + λB

Сложение матриц

Складывать можно только матрицы одинакового размера.

Сложение матриц есть операция нахождения матрицы , все элементы которой равны попарной сумме всех соответствующих элементов матриц 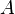и , то есть каждый элемент матрицы равен

Свойства сложения матриц:

• 1.коммутативность: A+B = B+A;

• 2.ассоциативность: (A+B)+C =A+(B+C);

• 3.сложение с нулевой матрицей: A + Θ = A;

• 4.существование противоположной матрицы: A + (-A) = Θ;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образует линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.

Умножение матриц

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

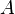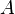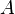Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность , — , то размерность их произведения есть .

Свойства умножения матриц:

• 1.ассоциативность (AB)C = A(BC);

• 2.некоммутативность (в общем случае): AB BA;

• 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

• 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

• 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

2 Определитель матрицы. Основные свойства определителя.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. — строчки матрицы, — определитель такой матрицы.
• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
• Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
• Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
• С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

3 Методы вычисления определителей. Надеюсь не попадется

Используя основные свойства определителей, вычисление можно осуществить одним из следующих способов.

1. Метод понижения порядка. Нахождение определителя n-го порядка сводится к вычислению п определителей (n – 1)-го порядка. Метод неэффективен.

2. Нахождение определителя сводится к вычислению одного определителя (n – 1)-го порядка. Для этого достаточно все элементы, кроме одного, в каком-либо столбце (строке) сделать равными нулю.

3. Приведение определителя к треугольному виду. Состоит в таком его преобразовании, когда все элементы, лежащие по одну сторону главной диагонали, становятся нулями. Полученный определитель равен произведению элементов главной диагонали

4 Обратная матрица. Нахождение обратной матрицы

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы

Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.Вторая матрица после применения всех операций станет равна , то есть будет искомой. Сложность алгоритма — .

Итерационные методы

Методы Шульца

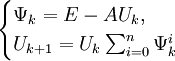
Оценка погрешности

Примеры

Матрица 2х2

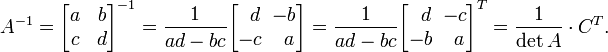
Обращение матрицы 2х2 возможно только при условии, что .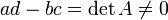

5 Решение системы линейных уравнений методом Крамера.

Описание метода

Для системы 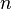линейных уравнений с 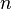неизвестными (над произвольным полем)

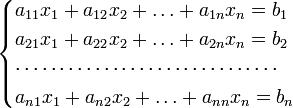
с определителем матрицы системы 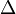, отличным от нуля, решение записывается в виде

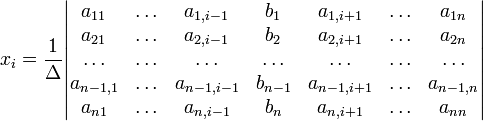
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

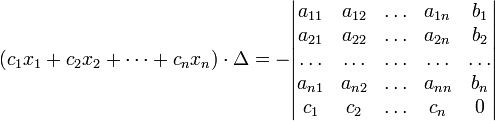
В этой форме формула Крамера справедлива без предположения, что 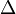отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы 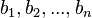и 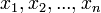, либо набор 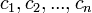состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений:

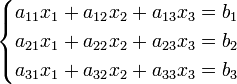
Определители:

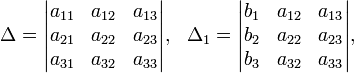
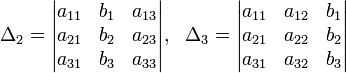
Решение:

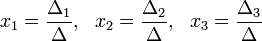
Пример:

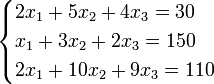
Определители:

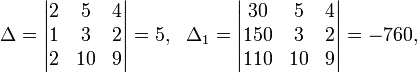
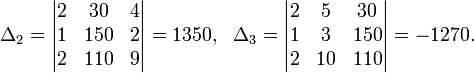
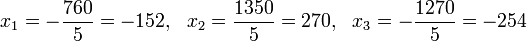
6 Решение системы линейных уравнений методом обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

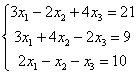
Решение: Запишем систему в матричной форме:
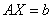, где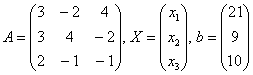

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице 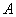нужно было бы поставить нули.

Решение системы найдем по формуле 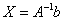(её подробный вывод можно посмотреть в статье Матричные уравнения).

Согласно формуле нам нужно найти обратную матрицу 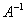и выполнить матричное умножение 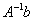. Алгоритм нахождения обратной матрицы подробно разобран на уроке Как найти обратную матрицу?

Обратную матрицу найдем по формуле:
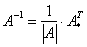, где 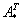– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

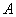Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если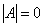 , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решаетсяметодом исключение неизвестных (методом Гаусса).

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров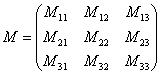

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

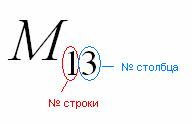
То есть, двойной подстрочный индекс указывает, что элемент 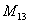находится в первой строке, третьем столбце, а, например, элемент 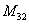находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

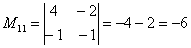
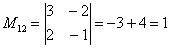
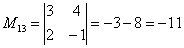
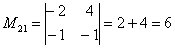
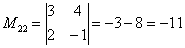
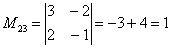
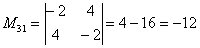
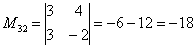
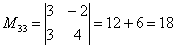
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).

Таким образом:

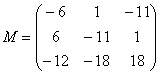– матрица миноров соответствующих элементов матрицы .

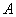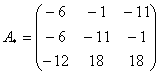– матрица алгебраических дополнений.

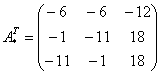– транспонированная матрица алгебраических дополнений.

Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?

Теперь записываем обратную матрицу:

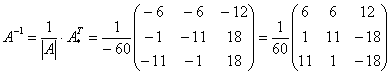
Ни в коем случае не вносим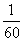 в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Осталось провести матричное умножение. Умножать матрицы можно научиться на уроке Действия с матрицами. Кстати, там разобран точно такой же пример.

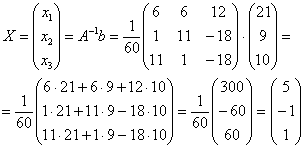
Обратите внимание, что деление на 60 выполняется в последнюю очередь.
Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.

Ответ: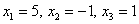

Пример 12

Решить систему с помощью обратной матрицы.

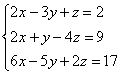
7 Решение системы линейных уравнений методом Гаусса.

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Описание метода

Пусть исходная система выглядит следующим образом

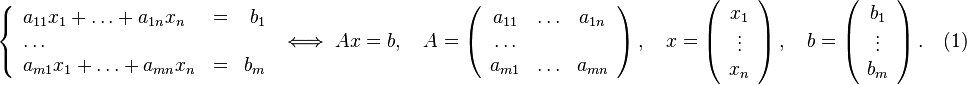
Матрица 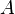называется основной матрицей системы, 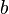— столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):

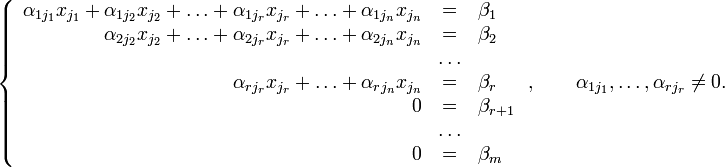
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных 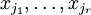^[3].

Тогда переменные 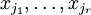называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число 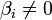, где 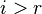, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.

Пусть 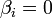для любых .

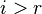Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 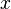( 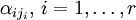, где 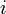— номер строки):

,
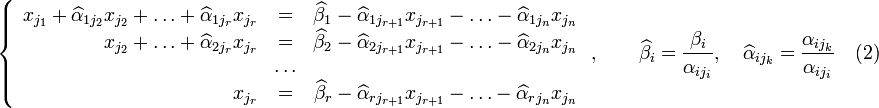где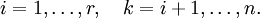

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Пример

Покажем, как методом Гаусса можно решить следующую систему:

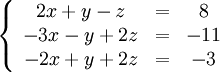
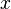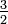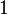Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

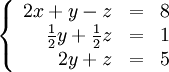
Теперь обнулим коэффициент при 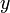в третьей строке, вычтя из неё вторую строку, умноженную на :

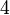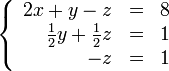
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

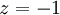из третьего;

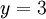из второго, подставив полученное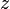

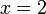из первого, подставив полученные 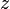и .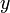

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

8 Понятие функции, область определения и множество значений функции.

Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной 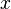однозначно определяет значение выражения 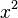, а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

авигация, поиск

Область определения функции — множество, на котором задаётся функция.

Областью определения функции 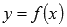(выражения f(x) ) называют множество всех значений x , для которых функция (выражение) имеет смысл.

Область определения функции 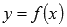обозначается как 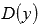или .

Дальнейшее изложение предполагает знание областей определения основных элементарных функций, знание классификации элементарных функций , а так же умение решать различные виды неравенств и систем неравенств.

При нахождении области определения функции приходится решать различные неравенства (иррациональные, логарифмические, тригонометрические и т.п.) и системы неравенств. Мы не будем подробно останавливаться на их решении, а иногда и вовсе будем оставлять без решения, так как это выходит за рамки данного раздела.

Что указывает на наличие ограничений области определения:

1. присутствие корней четной степени вида 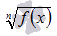, где n - четное, например, 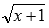(наличие степенной функции с дробным показателем, знаменатель которого есть четное число, например, 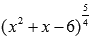); Примеры нахождения области определения степенной функции...
2. присутствие функции логарифма вида 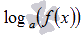, например, 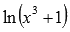или 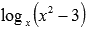; Нахождение области определения логарифмической функции...
3. присутствие дробей вида 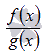, например, 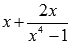; Нахождение области определения дроби...
4. присутствие функций тангенса вида 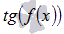и котангенса вида 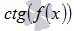, например, 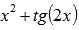или 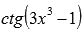; Примеры нахождения области определения тангенса и котангенса...
5. присутствие функций арксинуса вида 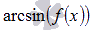и арккосинуса вида 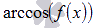, например, 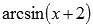или 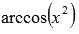; Примеры нахождения области определения арксинуса и арккосинуса...
6. присутствие показательно степенных функций вида 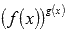, например, 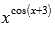; Нахождение области определения показательно степенной функции...
7. присутствие любых комбинаций всех вышеперечисленных случаев, например, 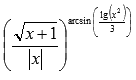Нахождение области определения элементарных функций...

Как находить область определенияв каждом случае.

Сначала будем считать функции y=f(x) и y=g(x) - основными элементарными функциями, чтобы разобраться с принципом нахождеия области определения.

В седьмом пункте рассмотрим случаи, когда y=f(x) и y=g(x) элементарные функции, то есть случаи, когда y=f(x) и y=g(x) представляют из себя сложные функции и их комбинации.

1. Для функций вида 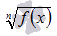, где n - четное, область определения находится из системы:
   

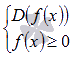
Пример.

Найти область определения функции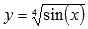

Решение.

Записываем систему

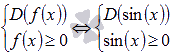
Как известно из свойств основных элементарных функций, область определения синуса есть все действительные числа, следовательно, система примет вид:

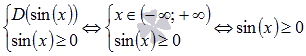
Решение последнего неравенства и даст искомую область определения.

Ответ:

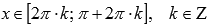
9 Способы задания функций, классификация функций

Табличный способ - общеизвестен (таблицы логарифмов, квадратных корней и т. д.). Он сразу дает числовое значение функции. В этом его преимущество перед другими способами. Недостатки: таблица трудно обозрима в целом; она часто не содержит всех нужных значений аргумента.

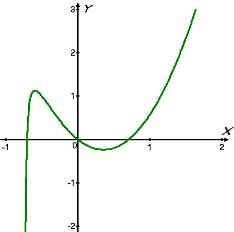
Графический способ состоит в построении линии (графика) в разных системах координат, например в Декартовой – абсциссы (по горизонтали) изображают значения аргумента, а ординаты (по вертикали) - соответствующие значения функции. Часто бывает, что функция быстро стремится вверх или вниз, поэтом тогда удобнее масштабы на осях брать разными.

Преимущества графического способа — легкость обозрения в целом и непрерывность изменения аргумента; недостатки: ограниченная степень точности и утомительность прочитывания значений функции с максимально возможной точностью.

Аналитический способ состоит в задании функции одной или несколькими формулами, например,

y=f(x)

. Если зависимость между х и у выражена уравнением, разрешенным относительно у, то величина у называется явной функцией аргумента х, в противном случае — неявной. Преимущество здесь в том, что всегда можно вычислить точно значение для любого аргумента. Недостатки, что по самой формуле сложно понять общее поведение функции.

Теперь вы знаете основные методы, и можете использовать любой тот, какой будет удобнее для вас при решении конкретной задачи. Вот, например, вы хотите зарабатывать на форекс, и вам надо проанализировать состояние рынка, спрогнозировать будущее тенденции. То для начала вы таблично выводите уже имеющие данные, потом по ним ищите аналитический вид и график, по которому и делаете необходимые выводы.

На продолжение предыдущего поста о способах задания функций сегодня поговорим о их классификации. Правда для полного понятие этих видов нужны широкие знания азов математического анализа, я постараюсь оговорить это в общем, а может где-то потом остановлюсь более подробно.

Для начала рассмотрим однозначные и многозначные. Если каждому значению аргумента соответствует одно значение функции, то она называется однозначной; если два или больше, - то многозначной (двузначной, трехзначной и т. д.). Когда особо не оговорено, что она многозначна, подразумевается, что - однозначна.

Также те, которые представленные формулами, подразделяются на явные и неявные. Их определение я давал в предыдущей статье, поэтому не буду повторяться.

Ещё бывают элементарные и неэлементарные. Последнее подразделение носит скорее исторический, чем математический характер. Каждая из основных элементарных функций представляет некоторое «действие» над аргументом (возведение в квадрат, извлечение кубического корня, логарифмирование, нахождение синуса и т. д.). Путем повторного выполнения этих действий, а также четырех основных операций арифметики (в ограниченном числе) получаются новые; они также причисляются к элементарным. Те, которые нельзя выразить указанным способом, считаются неэлементарными.

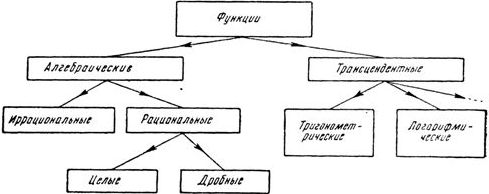
И на конец, они могут быть алгебраические и трансцендентные. Точное определение алгебраической функции можно дать лишь на основе более тонких понятий, таких как непрерывности или дифференцируемости. О них мы поговорим где-то в следующих постах, так как здесь надо знать ещё много разных дополнительных понятий, которые предварительно надо объяснить.

10 Основные свойства функций

Основные свойства функции.

1. Четность и нечетность

Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)

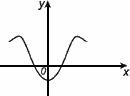
График четной функции симметричен относительно оси 0y

Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)

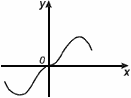
График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом 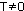, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

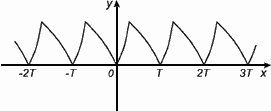
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)< f(x₂).

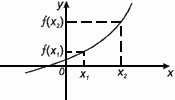
Функция f(x) убывает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁) > f(x₂).

4. Экстремумы

Точка Х_max называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Х_max , выполнено неравенство f(х) 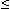f(X_max).

Значение Y_max=f(X_max) называется максимумом этой функции.

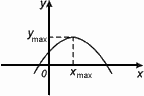
Х_max – точка максимума
У_max – максимум

Точка Х_min называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Х_min , выполнено неравенство f(х) 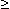f(X_min).

Значение Y_min=f(X_min) называется минимумом этой функции.

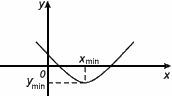
X_min – точка минимума
Y_min – минимум

X_min, Х_max – точки экстремума
Y_min, У_max – экстремумы.

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

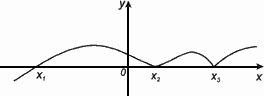
Х₁,Х₂,Х₃ – нули функции y = f(x).

11 Приращение аргумента и приращение функции. Разностное отношение

На оси Х – две точки: x₀ и x₁ (рис.1). Если от x₁ отнимем x₀, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x₀ в точке x₁. Эта разность между двумя заданными точками оси X и называется приращением аргумента.

Точки x₀ и x₁ образуют на оси Y соответственно точки у₀ и у₁. Если от у₁ отнять у₀, то мы получим приращение функции.

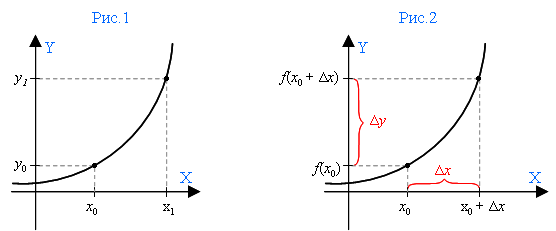
Итак, в функции y = f(x) относительно определенных точек x₀ и x₁:
разность x₁ – x₀ называется приращением аргумента, а разность у₁ – у₀ называется приращением функции.

Но у₀ и у₁ – зависимые переменные (зависимые от значений х). То есть их правильно записывать так: f(x₀) и f(x₁). Следовательно, приращение функции – это разность f(x₁) – f(x₀).

Приращение обозначается греческой буквой Δ (дельта):

Δx = x₁ – x₀;

Δy (или Δ f) = f(x₁) – f(x₀).

Можно сказать и иначе: если к x₀ прибавить величину приращения Δx, то мы получим точку x₁.
То есть x₁ = x₀ + Δx (рис.2).
Тогда точку f(x₁), отмеченную на первом рисунке как у₁, тоже можно обозначить иначе:
f(x₀ + Δx).

Осталось вывести формулу приращения функции.

Формула приращения функции:

Δy = f(x0 + Δx) – f(x0) или Δf = f(x0 + Δx) – f(x0)

Пример: Дана функция y = x². На оси абсцисс – две точки:
х₀ = 3,
(х₀ + Δx) = 4.
Надо найти приращение функции при переходе от точки х₀ к точке (х₀ + Δx).

Решение.

Итак, мы хотим найти Δy.

Сначала определимся с функцией:
так как у = f(x), то f(x) = x².

Теперь вычисляем приращение аргумента:
Δx = (х₀ + Δx) – х₀ = 4 – 3 = 1

Находим значения функции при х₀ = 3 и (х₀ + Δx) = 4:
f(x₀) = f(3) = 3² = 9
f(x₀ + Δx) = f(4) = 4² = 16

Осталось найти приращение функции:
Δy = f(x₀ + Δx) – f(x₀) = f(4) – f(3) = 16 – 9 = 7.

Ответ: Δy = 7.

12 Понятие производной. Понятие дифференциала.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется ее дифференциалом (в данной точке).

Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке. Производные элементарных функций.

13 Геометрический и физический смысл производной

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке