Частотные характеристики конечного отрезка линии
Уравнения конечного отрезка линии получаются из уравнений его участка (38) и (39) при x = l
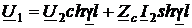 ,
,
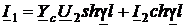 ;
;
(здесь для краткости записи введены обычные сокращения: U(l) = U1 и I(l) = I1).
Сравнивая эту пару выражений с уравнениями четырёхполюсника в А-параметрах
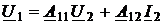 ,
,
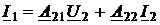 ,
,
заключаем, что отрезок однородной линии является неавтономным симметричным четырёхполюсником с матрицей А-параметров
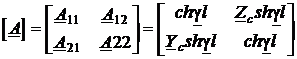 ,
,
детерминант которой, как и положено, равен единице.
В таком случае при произвольной пассивной нагрузке Uн = Zн Iн или Ií = Yн Uн он может быть представлен своими входными и передаточными комплексными частотными характеристиками. Для упрощения последующего анализа под нагрузкой будем понимать гипотетическую пассивную ветвь, параметры Zн и Yн которой при любых значениях частоты удовлетворяют условиям согласования Zн(jw) = Zc(jw) или Yн(jw) = Yc(jw). Такое ограничение является разумным, поскольку учёт отражений от нагрузки привёл бы лишь к неоправданному в учебном курсе усложнению анализа. Фактически же это условие означает замену сосредоточенной нагрузки отрезка линии полубесконечным отрезком той же линии. Поэтому при выводе выражений комплексных частотных характеристик конечного отрезка линии можно, минуя теорию четырёхполюсников, обратиться непосредственно к результатам анализа полуограниченного отрезка линии.
Входные комплексные частотные характеристики.
При введённом выше ограничении на характер нагрузки входные комплексные характеристики конечного (Рис. 9) и полубесконечного (Рис. 3) отрезков линии совпадают:
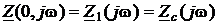 ,
,
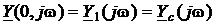 ,
,
Графики изменения от частоты w модулей и аргументов характеристического сопротивления Zc(jw) и характеристической проводимости Yc(jw) приведены выше на Рис. 30 и 32.
Передаточные комплексные частотные характеристики.
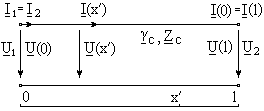 Рис. 32 Рис. 32 |
Для конечного отрезка линии выберем новую систему координат, показанную на Рис. 32. Если теперь в уравнения полубесконечного отрезка линии (18) и (19) вместо x¢ подставить длину отрезка линии l и положить U(l) = U2, I(l) = I2, то получим уравнения конечного согласованного отрезка линии в двух представлениях:
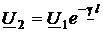 ,
,  ,
,
либо
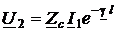 ,
, 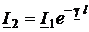 ,
,
в которых постоянная распространения 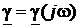 определена формулой (9):
определена формулой (9):
Отсюда в соответствии с определениями, находим следующие выражения различных видов передаточных характеристик согласованного отрезка линии:
· коэффициент передачи по напряжению 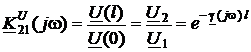 ;
;
· коэффициент передачи по току 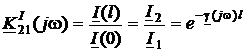 ;
;
· передаточное сопротивление 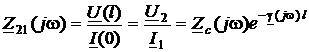 ;
;
· передаточная проводимость 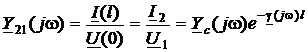 .
.
Из этих выражений видно, что передаточные характеристики согласованного отрезка однородной линии определяются, естественно, только частотными зависимостями характеристических параметров линии. Графики изменения от частоты w (в логарифмическом масштабе) модулей и аргументов характеристического сопротивления Zc(jw) и характеристической проводимости Yc(jw) даны на Рис. 31 и 32.
На Рис. 33 построены частотные зависимости коэффициентов затухания  и фазы
и фазы 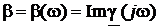 для некоторого частного примера с заданными значениями первичных параметров линии и диапазона частот. Из графика a = a(w) видно, что волны напряжения и тока разных частот в отрезке линии затухают по разному.
для некоторого частного примера с заданными значениями первичных параметров линии и диапазона частот. Из графика a = a(w) видно, что волны напряжения и тока разных частот в отрезке линии затухают по разному.
Фазовая скорость vф волн гармонических составляющих напряжения и тока определяется известной формулой
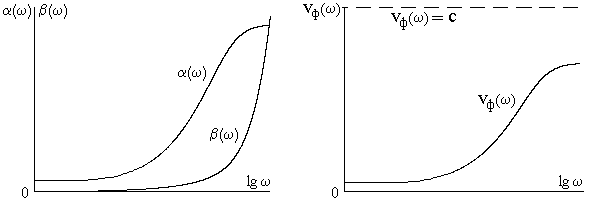 Рис. 33 Рис. 34 Рис. 33 Рис. 34 |
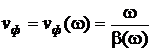 .
.
Рис. 34 иллюстрирует эту формулу для предыдущего частного примера линии передачи в том же диапазоне изменения частоты.
Зависимость коэффициента затухания a и фазовой скорости vф от частоты имеет большое практическое значение. При передаче по отрезку диссипативной линии сигнала (напряжения и тока), всегда состоящего из спектра частот, его энергия распределяется между группами волн напряжения и тока, соответствующих спектральному составу сигнала. Волны напряжения и тока отдельных гармонических составляющих спектра движутся по отрезку линии с разными значениями фазовой скорости и неодинаково затухают, поэтому форма сигнала при его движении вдоль отрезка непрерывно деформируется – искажается. В результате форма принимаемого сигнала(в конце отрезка линии) получается отличной от формы передаваемого сигнала (в начале отрезка). Напомним, что изменения формы сигнала, обусловленные неравномерностью коэффициента затухания a = a(w) и нелинейностью коэффициента фазы b = b(w) называются соответственно амплитудно-частотными и фазо-частотными искажениями.
Для неискажающей передачи сигналов требуется, чтобы коэффициент затухания a не зависел от частоты, а коэффициент фазы b был прямо пропорционален частоте (в последнем случае фазовая скорость 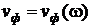 получается не зависящей от частоты). Преобразуя формулу (9) для постоянной распространения
получается не зависящей от частоты). Преобразуя формулу (9) для постоянной распространения 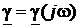 c учётом условия Хевисайда (84), нетрудно получить выражения коэффициентов затухания и фазы неискажающей линии:
c учётом условия Хевисайда (84), нетрудно получить выражения коэффициентов затухания и фазы неискажающей линии:
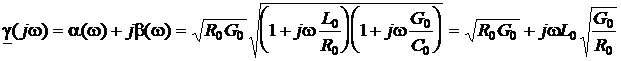
или
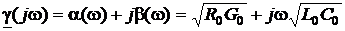 .
.
Следовательно:
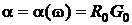
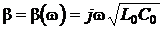 .
.
Поскольку коэффициент фазы b пропорционален частоте, то фазовая скорость vф волн всех гармоник напряжения и тока не зависит от неё и выражается формулой
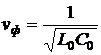 ,
,
определяющей также фазовую скорость волн в отрезке линии без потерь.
Следует отметить, что неискажающая линия является одновременно и линией с минимально возможным значением коэффициента затухания при фиксированных значениях параметров R0 и G0. Действительно, при высоких частотах (wL0 >> R0, wC0 >> G0) коэффициент затухания можно представить суммой
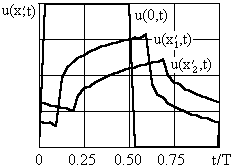 Рис. 35 Рис. 35 |
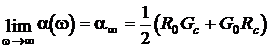 ,
,
из которой видно, что при
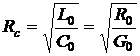 или
или 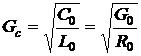
коэффициент затухания принимает минимальное значение, равное
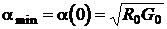 .
.
Для некоторого частного примера на Рис. 35 показаны кривые изменения напряжения 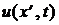 в течение периода их колебаний (0 £ t £ T) в трёх равноотстоящих сечениях полубесконечного отрезка однородной линии (Рис. 3):
в течение периода их колебаний (0 £ t £ T) в трёх равноотстоящих сечениях полубесконечного отрезка однородной линии (Рис. 3): 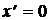 ,
, 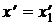 и
и 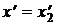 (
( 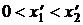 ).
).
В заключение отметим, что отрезок однородной линии конечной длины не может быть, вообще говоря, согласован в сравнительно широком диапазоне частот, так как частотные зависимости сопротивления и проводимости генератора и нагрузки и соответствующих характеристических параметров линии неодинаковы. В результате, из-за многократных отражений от начала и конца отрезка, частотные искажения напряжения и тока проявляются ещё более отчётливо, чем в условиях принятого выше ограничения характера нагрузки.
Оглавление
1. ВВЕДЕНИЕ...........................................................................................
2. ДИНАМИЧЕСКИЕ ПОГОННЫЕ ХАРАКТЕРИСТИКИ ЛИНИИ (ТЕЛЕГРАФНЫЕ УРАВНЕНИЯ).........................................................
3. КОМПЛЕКСНЫЕ ПОГОННЫЕ ХАРАКТЕРИСТИКИ ЛИНИИ (КОМПЛЕКСНЫЕ ТЕЛЕГРАФНЫЕ УРАВНЕНИЯ).........................
4. КОМПЛЕКСНЫЕ ХАРАКТЕРИСТИКИ ПОЛУБЕСКОНЕЧНОГО ОТРЕЗКА ОДНОРОДНОЙ ЛИНИИ.......................................................................
4.1. Общее решение комплексных телеграфных уравнений................
4.2. Определение граничных значений напряжения и тока...............
4.3. Волны напряжения и тока............................................................
5. КОМПЛЕКСНЫЕ ХАРАКТЕРИСТИКИ КОНЕЧНОГО ОТРЕЗКА ОДНОРОДНОЙ ЛИНИИ.....................................................................
5.1. Общее решение комплексных телеграфных уравнений..............
5.2. Определение граничных значений напряжения и тока отрезка линии
5.3. Распределения действующих значений напряжения и тока.......
5.4. Распределения составляющих сопротивления и проводимости.
6. АНАЛИЗ СТАЦИОНАРНОГО СОСТОЯНИЯ ОТРЕЗКА ЛИНИИ С ПОТЕРЯМИ..............................................................................................................
7. АНАЛИЗ ГАРМОНИЧЕСКОГО ПРОЦЕССА В ОТРЕЗКЕ ЛИНИИ БЕЗ ПОТЕРЬ..............................................................................................................
7.1. Комплексные характеристики отрезков линии без потерь.........
7.2. Гармонические волны напряжения и тока...................................
7.3. Распределения действующих значений напряжения и тока.......
7.4. Распределения составляющих сопротивления и проводимости.
7.5. Применение отрезков линии в качестве элементов согласующих устройств
8. КОМПЛЕКСНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ОТРЕЗКА ОДНОРОДНОЙ ЛИНИИ.....................................................................
8.1. Частотные характеристики полубесконечного отрезка линии...
8.2. Частотные характеристики конечного отрезка линии................
[*] См., например, Л.И.Мандельштам. Лекции по теории колебаний. - М.: 1972. - 471 с.
[†] Явное нарушение взаимной дуальности формул для Z(x) и Y(x) обусловлено тем, что во всех выражениях, начиная с (36), вместо коэффициентов отражения по напряжению ru2 и току ri2 фактически, в силу соотношения между ними (35), используется только один: коэффициент отражения по напряжению, переобозначенный как r.
[‡] Это нетрудно доказать, например, с помощью теоремы косинусов.
