Распределения составляющих сопротивления и проводимости
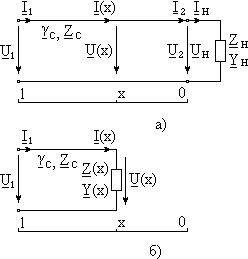 Рис. 18 Рис. 18 |
При исследовании гармонических процессов в отрезках линии, при расчёте согласующих распределённых устройств и в других приложениях большой интерес представляют выражения входного сопротивления Z(x) и входной проводимости Y(x) участка [0, x] отрезка линии (0 £ x £ l). Участок отрезка однородной линии вместе с пассивной нагрузкой справа от сечения с координатой x (Рис. 18, а) можно заменить пассивной ветвью (Рис. 18, б), причём распределения напряжения и тока в остальной части отрезка линии не изменятся, если значения сопротивления Z(x) и проводимости Y(x) участка вычислить по определённым формулам. Выражения комплексных входных параметров участка конечного отрезка линии Z(x) и Y(x) зависят от вида его исходных комплексных характеристик и граничных условий на его конце.
Возьмём, к примеру, комплексные характеристики участка конечного отрезка в экспоненциальных функциях в виде (36) - (37). По определению
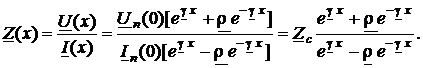 (44)
(44)
Применив подстановку (43), получим отсюда формулу
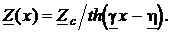 (45)
(45)
Аналогичным образом выводятся формулы для Y(x):
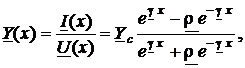 (46)
(46)
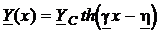 [†].(47)
[†].(47)
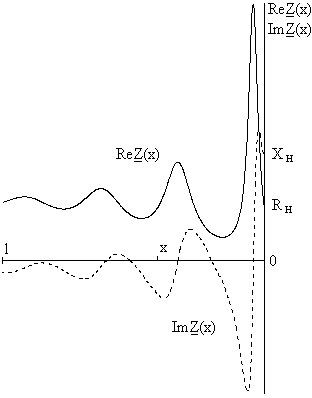 Рис. 19 Рис. 19 |
Если обратиться к выражениям комплексных характеристик участка конечного отрезка линии в гиперболических функциях (38) - (39), то при учёте граничных условий для конца отрезка (40) - (41) получаем одно из возможных выражений 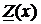 :
:
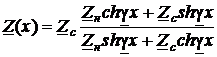 .(48)
.(48)
В соответствии с принципом дуальности
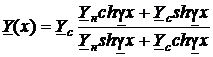 .(49)
.(49)
Анализ полученных выражений в общем виде довольно сложен, поэтому мы ограничимся иллюстрацией зависимостей Re Z(x), Im Z(x) и Re Y(x), Im Y(x) для некоторого частного примера с заданными значениями параметров нагрузки Zн или Yн, постоянной распространения линии 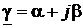 и длины l её отрезка (Рис. 19 и 20).
и длины l её отрезка (Рис. 19 и 20).
Построенные графики показывают, что составляющие входных параметров участка конечного отрезка однородной линии Re Z(x), Im Z(x) и Re Y(x), Im Y(x) изменяются не монотонно, а с колебаниями, причём эти колебания происходят относительно значений Re Zc, Im Zc и Re Yc, Im Yc. С удалением от конца отрезка размах колебаний уменьшается, что объясняется падением влияния отражённых волн напряжения и тока. В результате значения входных параметров участка всё более определяются комплексами действующих значений падающих волн напряжения и тока. Такое объяснение подтверждается формулами для комплексных входных параметров участка конечного отрезка однородной линии. В частности, из формул (44) - (47) следует, что при 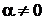 и неограниченном возрастании длины участка x значения его сопротивления и проводимости стремятся к характеристическим:
и неограниченном возрастании длины участка x значения его сопротивления и проводимости стремятся к характеристическим:
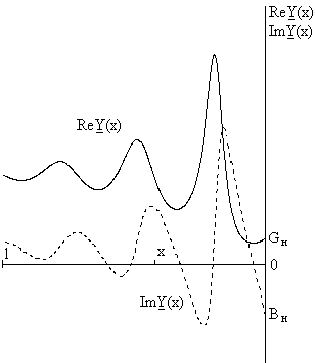 Рис. 20 Рис. 20 |
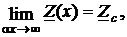
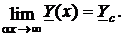
Размах колебаний зависит, конечно, и от соотношений значений параметров нагрузки и характеристических параметров Zc и Yc, иначе говоря от значения коэффициента отражения 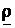 . Чем меньше рассогласование, тем колебания значений составляющих входных параметров участка менее заметны. При согласованной нагрузке Zн = Zc или Yн = Yc, отражённых волн напряжения и тока нет и r = 0; а из формул (44) - (47) следует
. Чем меньше рассогласование, тем колебания значений составляющих входных параметров участка менее заметны. При согласованной нагрузке Zн = Zc или Yн = Yc, отражённых волн напряжения и тока нет и r = 0; а из формул (44) - (47) следует 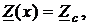
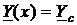 .
.
Из графиков Рис. 19 и Рис. 20 также видно, что при некоторых значениях координаты сечения x отрезка линии значения входных параметров участка оказываются вещественными. Такие значения координаты называют резонансными.
Примечания:
1. При коротком замыкании конца отрезка однородной линии длиной l ( 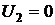 или, формально,
или, формально, 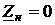 ) из формул (48) и (49) при
) из формул (48) и (49) при 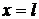 следует:
следует:
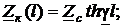 (50)
(50)
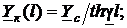 (51)
(51)
при I2= 0 или, формально, Yн = 0 (режим холостого хода отрезка линии) из тех же формул получается
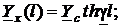 (52)
(52)
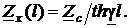 (53)
(53)
Выражениям (48) и (49) входных параметров отрезка линии при 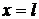 и учёте (50 - 53) путём элементарных преобразований можно придать вид:
и учёте (50 - 53) путём элементарных преобразований можно придать вид:
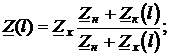
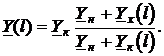
Этими формулами удобно пользоваться, если известны (например, из эксперимента) значения комплексных входных параметров в предельных режимах (короткого замыкания и холостого хода).
2. Из первых четырёх выражений предыдущего примечания имеем
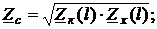
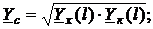
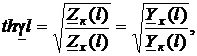
где 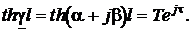
В свою очередь из последнего соотношения получаем
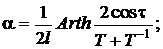
для T > 1 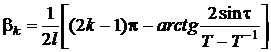 ;
;
для T < 1 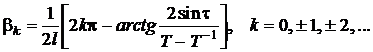 ;
;
Ввиду того, что значение коэффициента b определяется неоднозначно, при его вычислении необходима проверка на соответствие неравенству
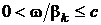 = 3×108 м/с.
= 3×108 м/с.
Минимальное значение bk, удовлетворяющее этому неравенству, определяет лишь одно допустимое – максимальное – значение фазовой скорости волн напряжения и тока. Сделать выбор среди всех её других возможных значений, опираясь лишь на результатах измерения комплексных входных параметров отрезка линии в предельных режимах, нельзя.
3. По известным значениям характеристических параметров однородной линии легко найти и значения её первичных или погонных параметров, если воспользоваться их определениями (9), (14) и (17). Откуда
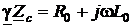 ;
; 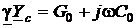 .
.
Каждое из этих комплексных равенств распадается на два вещественных; при заданном значенииw полученные четыре уравнения решаются относительно R0, L0, G0 и L0.
На практике часто, в особенности при высоких частотах, значения потребляемой мощности в начале и в конце отрезка линии передачи близки. Тогда в любом режиме такой отрезок линии передачи удовлетворительно моделируется отрезком однородной линии без потерь. В отличие от неё модель, являвшаяся до сих пор объектом исследования, называют линией с потерями, а линию без потерь считают её подвидом. Применение такой, довольно грубой модели, можно считать обоснованным, если собственное затухание отрезка линии передачи al в согласованном режиме не превышает 0,045 Нп; при этом 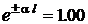 с погрешностью не более 5%, и характеристики участка существенно упрощаются. Разновидности гармонического процесса в отрезке линии без потерь будут рассмотрены особо.
с погрешностью не более 5%, и характеристики участка существенно упрощаются. Разновидности гармонического процесса в отрезке линии без потерь будут рассмотрены особо.
В отсутствие предварительной информации о характере процессов в отрезке линии или если эти процессы выступают в своей совокупности, пользуются самой общей и потому наиболее сложной моделью – однородной линией с потерями.
