Комплексные погонные характеристики линии (комплексные телеграфные уравнения)
При возбуждении отрезка линии источником гармонического напряжения или тока с частотой w установившиеся ток и напряжение его любого сечения изменяются также по гармоническому закону с тем же значением частоты w. В этом случае, как и в теории цепей с сосредоточенными элементами, все расчёты значительно упрощаются, если применить комплексный анализ. Согласно правилам комплексного анализа вещественным гармоническим функциям напряжения и тока можно однозначно поставить в соответствие комплексные экспоненциальные функции – комплексы мгновенных значений этих величин:
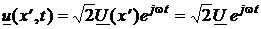 ,
, 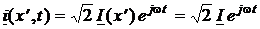 ,
,
над которыми и совершаются последующие линейные вещественные математические операции. Здесь U = U(x¢) и I = I(x¢) – комплексные функции вещественного аргумента x¢, называемые комплексами действующих значений напряжения и тока в сечении линии с координатой x¢.
Мгновенные значения этих величин вычисляются известным образом:
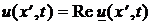 ,
, 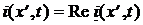 , (3)
, (3)
либо
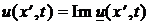 ,
, 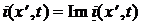 ,(4)
,(4)
в зависимости от вида вещественной гармонической функции времени, описывающей воздействие.
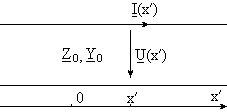 Рис. 2 Рис. 2 |
Подставляя комплексы мгновенных значений напряжения и тока в систему телеграфных уравнений (2), получаем систему двух обыкновенных дифференциальных уравнений первого порядка
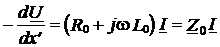 , (5)
, (5)
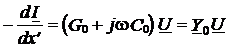 , (6)
, (6)
представляющих собой комплексные погонные характеристики (комплексные телеграфные уравнения) однородной линии (Рис. 2). Введённые здесь обозначения 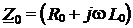 и
и 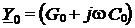 – это так называемые комплексные погонные параметры: продольное сопротивление и поперечная проводимость единицы длины однородной линии.
– это так называемые комплексные погонные параметры: продольное сопротивление и поперечная проводимость единицы длины однородной линии.
Преобразуем последнюю систему двух уравнений первого порядка к одному дифференциальному уравнению второго порядка относительно U = U(x¢) или I = I(x¢). Исключим, например, ток I = I(x¢). Дифференцируя первое уравнение и подставляя значение dI(x¢)/dx¢ из второго, найдём:
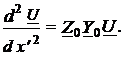 (7)
(7)
Точно такое же уравнение можно получить и для I = I(x¢):
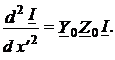 (8)
(8)
Введём комплексный параметр 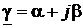 , называемый постоянной (коэффициентом) распространения и определяемый выражением
, называемый постоянной (коэффициентом) распространения и определяемый выражением
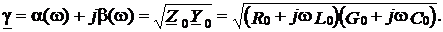 (9)
(9)
Для того, чтобы внести однозначность в определение g, условимся в дальнейшем выбирать то значение корня, которое располагается в первом квадранте плоскости комплексной переменной. Вещественная часть постоянной распространения 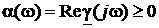 называется коэффициентом затухания, а мнимая
называется коэффициентом затухания, а мнимая 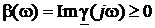 – коэффициентом фазы (волновым числом). Более детально смысл этих величин обсуждается ниже.
– коэффициентом фазы (волновым числом). Более детально смысл этих величин обсуждается ниже.
С введением постоянной распространения g комплексные телеграфные уравнения однородной линии примут вид:
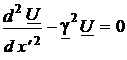 и
и 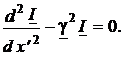 (10)
(10)
Уравнения такого вида в теории колебаний называют волновыми или уравнениями Гельмгольца.
Комплексные характеристики полубесконечного отрезка однородной линии
