Динамические погонные характеристики линии (телеграфные уравнения)
Введение
Одним из возможных способов анализа электромагнитных явлений в каком-либо устройстве является обращение к его математической модели в виде электрической цепи. Напряжение и ток каждого сосредоточенного элемента цепи в общем случае являются вещественными функциями лишь одной независимой переменной – относительного времени t. Цепи с сосредоточенными элементами (модели Кирхгофа) успешно отражают электромагнитные процессы в системах, размеры которых l1, l2, l3 пренебрежимо малы в сравнении с наименьшей значимой длиной волны:
(l1, l2, l3) << lmin = vф/fmax. (1)
Здесь 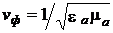 – фазовая скорость электромагнитной волны в безграничной среде с проницаемостями ea и ma вокруг исследуемой системы, а fmax – верхняя граница значимого частотного спектра воздействия. Как известно, математической основой анализа процессов в любой цепи с конечным числом сосредоточенных элементов является совокупность динамических характеристик всех элементов цепи и полная система её топологических уравнений, преобразуемая в систему обыкновенных дифференциальных уравнений состояния цепи. При этом выражения переменных состояния цепи находятся однозначно, если известны их начальные значения.
– фазовая скорость электромагнитной волны в безграничной среде с проницаемостями ea и ma вокруг исследуемой системы, а fmax – верхняя граница значимого частотного спектра воздействия. Как известно, математической основой анализа процессов в любой цепи с конечным числом сосредоточенных элементов является совокупность динамических характеристик всех элементов цепи и полная система её топологических уравнений, преобразуемая в систему обыкновенных дифференциальных уравнений состояния цепи. При этом выражения переменных состояния цепи находятся однозначно, если известны их начальные значения.
При теоретическом исследовании электромагнитных процессов в устройствах, для которых неравенства (1) не соблюдаются, применяют полевые модели (модели Максвелла), анализируемые методами теории электромагнитного поля (электродинамики).
Однако в ряде случаев все необходимые для практики сведения об электромагнитных свойствах исследуемых устройств можно получить и с помощью теории цепей, расширив соответствующим образом её элементную базу. Например, отрезки двухпроводных и коаксиальных линий, для которых выполняются соотношения:
(l1, l2) << lmin = vф/fmax
при l3 > lmax или l3 @ lmax ,
(где 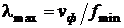 , а fmin - низшая граница значимого частотного спектра воздействия) в теории электрических цепей удовлетворительно моделируют одномерным распределённым четырёхполюсным элементом – отрезком двухпроводной линии передачи (модель Кирхгофа-Томсона).
, а fmin - низшая граница значимого частотного спектра воздействия) в теории электрических цепей удовлетворительно моделируют одномерным распределённым четырёхполюсным элементом – отрезком двухпроводной линии передачи (модель Кирхгофа-Томсона).
В дальнейшем ограничимся анализом процессов в цепях, содержащих отрезки только инвариантных во времени однородных линий. Последние служат моделями линий передач, у которых в продольном направлении неизменны и не зависят от времени конфигурация и значения электромагнитных параметров проводников и разделяющих их диэлектриков. В противном случае для моделирования используются отрезки неоднородных линий. На схемах электрических цепей отрезок однородной линии передачи изображают двумя параллельными отрезками прямых с обязательной фиксацией условно положительных направлений напряжения и тока его произвольного сечения (Рис. 1). Электрические цепи, содержащие хотя бы один распределённый элемент – отрезок линии – называют цепями с распределёнными элементами.
Комплексные характеристики полубесконечного отрезка однородной линии
Волны напряжения и тока
Перейдём к мгновенным значениям напряжения u(x¢, t) и тока i(x¢, t) в произвольном сечении отрезка с координатой x¢. Полагая в выражении (11) 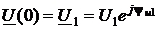 в соответствии, например, с формулами (3), получаем
в соответствии, например, с формулами (3), получаем
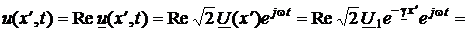
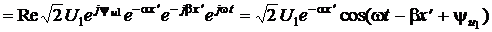 .
.
Отсюда видно, что при фиксированном значении координаты x¢ напряжение u(x¢, t) этого сечения является гармонической функцией времени с частотой w и постоянной амплитудой 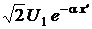 . Если же зафиксировать момент времени t и рассматривать изменение напряжения вдоль полубесконечного отрезка, то получим осциллирующую знакопеременную функцию амплитуда которой
. Если же зафиксировать момент времени t и рассматривать изменение напряжения вдоль полубесконечного отрезка, то получим осциллирующую знакопеременную функцию амплитуда которой 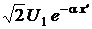 убывает по экспоненте с ростом x¢, то есть по мере удаления от начала отрезка линии.
убывает по экспоненте с ростом x¢, то есть по мере удаления от начала отрезка линии.
С течением времени распределение напряжения перемещается вдоль отрезка линии, образуя волну напряжения. Для определённости, за скорость распространения волны 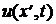 примем её так называемую фазовую скорость vф, под которой понимают скорость перемещения её сечения в выбранной неподвижной системе координат, фаза колебания в котором
примем её так называемую фазовую скорость vф, под которой понимают скорость перемещения её сечения в выбранной неподвижной системе координат, фаза колебания в котором 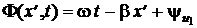 остаётся неизменной. Отсюда видно, что с течением времени t значение фазы волны остаётся неизменным, если значение координаты её сечения x¢ соответствующим образом возрастает. Таким образом, волна напряжения перемещается (бежит) от начала отрезка линии. Из условия постоянства значения фазы бегущей волны
остаётся неизменной. Отсюда видно, что с течением времени t значение фазы волны остаётся неизменным, если значение координаты её сечения x¢ соответствующим образом возрастает. Таким образом, волна напряжения перемещается (бежит) от начала отрезка линии. Из условия постоянства значения фазы бегущей волны 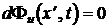 или
или
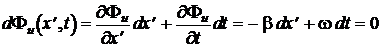
следует, что волна напряжения 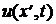 перемещается вдоль отрезка линии с фазовой скоростью
перемещается вдоль отрезка линии с фазовой скоростью
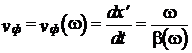
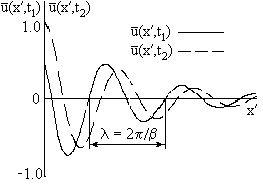 Рис. 7 Рис. 7 |
На Рис. 7 изображены нормированные на амплитуду Um волны напряжения для двух следующим друг за другом моментов времени t1и t2, причём 0 < t2 – t1 < T/2.
Аналогично можно рассмотреть изменения тока вдоль полубесконечного отрезка однородной линии и получить выражение
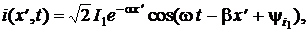
которое описывает волну тока, бегущую от начала отрезка с тем же значением фазовой скорости vф и так же затухающую в направлении своего распространения.
Из выражений волн напряжения 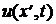 и тока
и тока 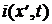 следует, что значение коэффициента затухания
следует, что значение коэффициента затухания 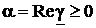 , входящего в показатель экспоненты, характеризует убывание амплитуд волн при их распространении вдоль отрезка линии. Фазы напряжения и тока изменяются вдоль отрезка линии по линейному закону. Коэффициент фазы b определяет скорость этих изменений. Разность фаз напряжения и тока в любом сечении отрезка равен аргументу характеристического сопротивления линии
, входящего в показатель экспоненты, характеризует убывание амплитуд волн при их распространении вдоль отрезка линии. Фазы напряжения и тока изменяются вдоль отрезка линии по линейному закону. Коэффициент фазы b определяет скорость этих изменений. Разность фаз напряжения и тока в любом сечении отрезка равен аргументу характеристического сопротивления линии
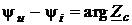 .
.
Коэффициент затухания a выражается в неперах или децибелах на единицу длины, а коэффициент фазы b – в радианах на единицу длины.
Убывание амплитуд волн напряжения и тока в направлении их перемещения обусловливается необратимыми преобразованиями энергии вдоль отрезка линии, а изменение их фаз – конечными значениями фазовых скоростей распространения этих волн.
Введение
Одним из возможных способов анализа электромагнитных явлений в каком-либо устройстве является обращение к его математической модели в виде электрической цепи. Напряжение и ток каждого сосредоточенного элемента цепи в общем случае являются вещественными функциями лишь одной независимой переменной – относительного времени t. Цепи с сосредоточенными элементами (модели Кирхгофа) успешно отражают электромагнитные процессы в системах, размеры которых l1, l2, l3 пренебрежимо малы в сравнении с наименьшей значимой длиной волны:
(l1, l2, l3) << lmin = vф/fmax. (1)
Здесь 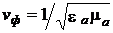 – фазовая скорость электромагнитной волны в безграничной среде с проницаемостями ea и ma вокруг исследуемой системы, а fmax – верхняя граница значимого частотного спектра воздействия. Как известно, математической основой анализа процессов в любой цепи с конечным числом сосредоточенных элементов является совокупность динамических характеристик всех элементов цепи и полная система её топологических уравнений, преобразуемая в систему обыкновенных дифференциальных уравнений состояния цепи. При этом выражения переменных состояния цепи находятся однозначно, если известны их начальные значения.
– фазовая скорость электромагнитной волны в безграничной среде с проницаемостями ea и ma вокруг исследуемой системы, а fmax – верхняя граница значимого частотного спектра воздействия. Как известно, математической основой анализа процессов в любой цепи с конечным числом сосредоточенных элементов является совокупность динамических характеристик всех элементов цепи и полная система её топологических уравнений, преобразуемая в систему обыкновенных дифференциальных уравнений состояния цепи. При этом выражения переменных состояния цепи находятся однозначно, если известны их начальные значения.
При теоретическом исследовании электромагнитных процессов в устройствах, для которых неравенства (1) не соблюдаются, применяют полевые модели (модели Максвелла), анализируемые методами теории электромагнитного поля (электродинамики).
Однако в ряде случаев все необходимые для практики сведения об электромагнитных свойствах исследуемых устройств можно получить и с помощью теории цепей, расширив соответствующим образом её элементную базу. Например, отрезки двухпроводных и коаксиальных линий, для которых выполняются соотношения:
(l1, l2) << lmin = vф/fmax
при l3 > lmax или l3 @ lmax ,
(где 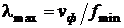 , а fmin - низшая граница значимого частотного спектра воздействия) в теории электрических цепей удовлетворительно моделируют одномерным распределённым четырёхполюсным элементом – отрезком двухпроводной линии передачи (модель Кирхгофа-Томсона).
, а fmin - низшая граница значимого частотного спектра воздействия) в теории электрических цепей удовлетворительно моделируют одномерным распределённым четырёхполюсным элементом – отрезком двухпроводной линии передачи (модель Кирхгофа-Томсона).
В дальнейшем ограничимся анализом процессов в цепях, содержащих отрезки только инвариантных во времени однородных линий. Последние служат моделями линий передач, у которых в продольном направлении неизменны и не зависят от времени конфигурация и значения электромагнитных параметров проводников и разделяющих их диэлектриков. В противном случае для моделирования используются отрезки неоднородных линий. На схемах электрических цепей отрезок однородной линии передачи изображают двумя параллельными отрезками прямых с обязательной фиксацией условно положительных направлений напряжения и тока его произвольного сечения (Рис. 1). Электрические цепи, содержащие хотя бы один распределённый элемент – отрезок линии – называют цепями с распределёнными элементами.
Динамические погонные характеристики линии (телеграфные уравнения)
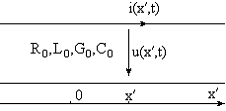 Рис. 1 Рис. 1 |
Отрезок однородной линии, как и всякий сосредоточенный элемент электрической цепи, определяется своими динамическими характеристиками, под которыми здесь понимают соотношения, связывающие напряжение и ток любого сечения отрезка в любой момент времени.
Выберем поэтому сначала координатную ось x¢, направив её по положительному направлению потока мощности, и отметим на ней произвольно начало отсчёта координаты сечения отрезка линии (Рис. 1).
Столь же произвольно зададимся началом отсчёта относительного времени t. И, наконец, обозначим для краткости через u = u(x¢, t) и i = i(x¢, t) мгновенные значения напряжения и тока в сечении линии с координатой x¢ в момент времени t.
Безупречный вывод динамических характеристик однородной линии возможен лишь на основе теории Максвелла [*]. Поэтому здесь приведём их без вывода и определим однородную линию системой двух дуальных линейных уравнений в частных производных первого порядка:
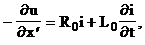
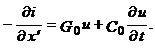 (2)
(2)
 Здесь R0, L0, G0 и C0 – независимые, так называемые первичные или погонные, то есть приходящиеся на единицу длины, параметры линии. Приведённая система однородных линейных уравнений, представляющая динамические погонные характеристики однородной линии, впервые была получена и исследована при теоретическом изучении электромагнитных явлений в линиях дальней телеграфной связи. Поэтому её традиционно называют системой телеграфных уравнений. Следует отметить, однако, что результаты анализа этих уравнений с помощью известной системы аналогий можно с успехом перенести и на другие виды цепей.
Здесь R0, L0, G0 и C0 – независимые, так называемые первичные или погонные, то есть приходящиеся на единицу длины, параметры линии. Приведённая система однородных линейных уравнений, представляющая динамические погонные характеристики однородной линии, впервые была получена и исследована при теоретическом изучении электромагнитных явлений в линиях дальней телеграфной связи. Поэтому её традиционно называют системой телеграфных уравнений. Следует отметить, однако, что результаты анализа этих уравнений с помощью известной системы аналогий можно с успехом перенести и на другие виды цепей.
Умножая первое уравнение системы на i, второе – на u и складывая, имеем
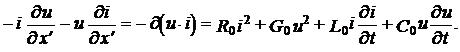
Проинтегрируем последнее равенство по x¢ в пределах от x¢1 до x¢2:
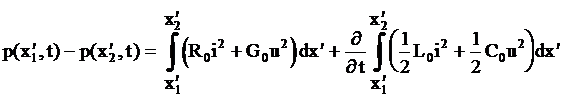
Величина p(x¢, t) = u×i определяет мгновенную мощность как скорость переноса энергии в положительном направлении оси x¢ через сечение линии с координатой x¢ в момент времени t.
Последнее равенство имеет простой физический смысл: сумма скоростей необратимого преобразования энергии и изменения электрической и магнитной энергии участка линии (x¢1, x¢2) в момент времени t равна разности мгновенных значений мощности в начале и в конце рассматриваемого участка в тот же момент времени. Оно представляет собой частный случай известной в электродинамике теоремы Пойнтинга: поток мощности выражается здесь произведением напряжения на ток.
Основная задача анализа процессов в однородной линии или её отрезке заключается в том, чтобы путём решения системы (2) в области определения x¢ найти распределения напряжения и тока вдоль линии или её отрезка в любой момент времени t ³ 0. Задача, однако, состоит не в том, чтобы определить бесконечное множество различных выражений мгновенных значений напряжения u = u(x¢, t) и тока i = i(x¢, t), удовлетворяющих системе телеграфных уравнений, а в том, чтобы найти такие функции, которые описывают напряжение и ток отрезка конкретной линии – распределённого компонента заданной цепи. А для этого надо поставить ряд дополнительных ограничений, выражаемых начальными и граничными (краевыми) условиями.
Начальные условия описывают распределение напряжения и тока вдоль линии или её отрезка накануне коммутации (t = 0-) и играют в данном случае такую же роль, что и начальные условия в цепях с сосредоточенными элементами, с той лишь разницей, что u(x¢, t) и i(x¢, t) зависят, вообще говоря, от некоторых функций u(x¢, 0-) и i(x¢, 0-), тогда как u(t) и i(t) любого элемента цепи с сосредоточенными элементами зависят от определённого числа начальных значений токов катушек, напряжений конденсаторов и задающих напряжений и токов.
Иной характер имеют граничные (краевые) условия. Они устанавливают функциональную связь между напряжением и током либо их выражения или значения в начале и в конце отрезка линии в любой момент времени t ³ 0. Граничные условия тесно связаны с доказательством теоремы существования и единственности решения телеграфных уравнений.
В результате достаточно длительного воздействия источников постоянного или периодически изменяющегося напряжения или тока отрезок линии придёт к установившемуся режиму, в котором напряжение и ток его любого сечения либо неизменны во времени (стационарное состояние), либо изменяются периодически. Изменение граничных условий отрезка линии вызовет изменение установившихся распределений напряжения и тока. Однако переход к новому установившемуся режиму, характеризуемому функциями uпр(x¢, t) и iпр(x¢, t), произойдёт не сразу. В отрезке линии возникнут свободные колебания напряжения и тока, которые описываются функциями uсв(x¢, t) и iсв(x¢, t). Как и в теории цепей с сосредоточенными элементами, будем считать, что во время переходного процесса напряжение и ток любого сечения отрезка линии получается сложением установившихся и свободных колебаний
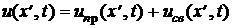 ,
, 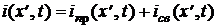 .
.
Функции принуждённых составляющих uпр(x¢, t) и iпр(x¢, t) выберем так, чтобы они удовлетворяли системе телеграфных уравнений и заданным граничным условиям. Тогда вторые составляющие – функции uсв(x¢, t) и iсв(x¢, t) – должны также удовлетворять телеграфным уравнениям и граничным условиям отрезка линии в цепи, “освобождённой” от активных элементов. Постоянные интегрирования могут быть вычислены из начальных условий после суммирования обеих составляющих напряжения и тока.
Несмотря на внешнюю простоту телеграфных уравнений, их аналитическое решение для произвольных граничных условий отсутствует.
В этой главе исследуются лишь установившиеся процессы в отрезках однородной линии. Поэтому в дальнейшем для упрощения записи индекс “пр” в обозначениях мгновенных, амплитудных и действующих значений напряжения и тока будет опущен.
Задача существенно облегчается при анализе гармонического процесса в отрезке линии, поскольку в этом случае известен закон изменения напряжения и тока во времени в произвольном сечении отрезка и остаётся лишь найти распределение их амплитуд и начальных фаз вдоль отрезка линии.
