Частотный критерий устойчивости Михайлова
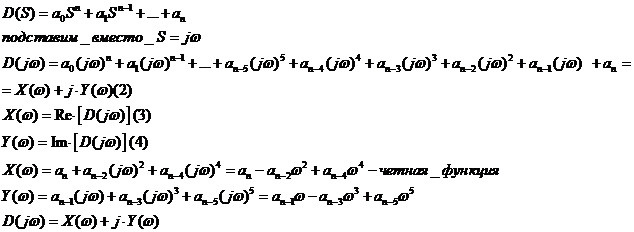
При изменении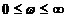 
конец вектора Михайлова будет вычерчивать кривую, которую назовем Годографом Михайлова
По поведению Годографа можно судить об устойчивости замкнутой АС.
Необходимое и достаточное условие устойчивости по Михайлову: Для устйочивости замкнутой АС необходимо и достаточно чтобы при изменении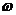 
Годограф:
-начинался на положительной вещественной оси( на оси х справа от нуля)
-изменялся в положительном направлении( против часовой стрелки)
-охватывать n- квадратов ( где n-порядок хар. уравнения- maxстепень в уравнении)
-уходить в бесконечность в n-м квадрате.
| Годографы Михайлова для устойчивой замкнутой АС. | Годографы Михайлова для неустойчивой замкнутой АС. |
 |  |
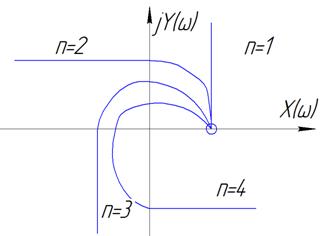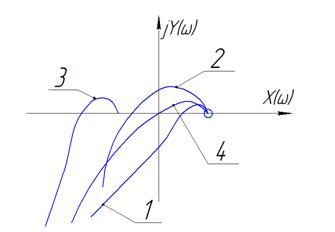Следствие из Критерия Михайлова:
1. 
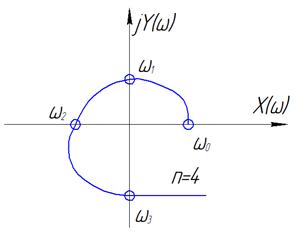Критерий чередуемости корней
Обозначим точки пересечения с осями через омега.
Частоты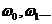 
являются корнями вещественной и мнимой частей годографа михайлова
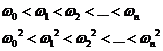
Для устойчивости замкнутой АС необходимо и достаточно чтобы корни вещественной и мнимой частей годографа чередовались
- Частотный критерий устойчивости Найквиста в случае устойчивой разомкнутой АС.
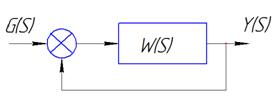
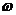При исследовании устойчивости считается по известной передаточной функции разомкнутой АС. Заменяем Sна j и тем самым получаем комплексную передаточную функцию (КПФ). При изменении 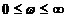вектор КПФ будет вычерчивать кривую – годограф КПФ. По виду этой кривой для разомкнутой АС можно судить о устойчивости замкнутой АС.
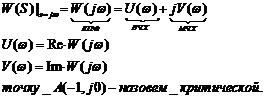
Существует 3случая исследования устойчивости по Найквисту:
1 случай: Разомкнутая АС устойчива
2 случай: Разомкнутая АС нейтрально устойчива (находится на границе устойчивости) и имеет в своем составе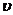 
интегрирующих звеньев.
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( mкорней характеристического уравнения с положительными вещественными частями.
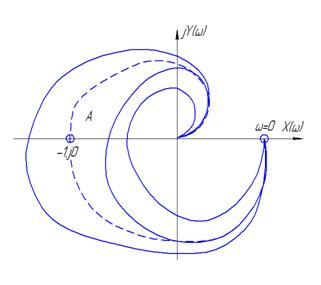
1 случай: Для устойчивости замкнутой АС. В случае устойчивой разомкнутой АС необходимо и достаточно, чтобы при изменении 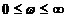Годограф КПФ разомкнутой АС (АФХ разомкнутой АС) не должен охватывать критическую точку..
-штриховая линия на рис.
- Частотный критерий устойчивости Найквиста при наличии в структуре разомкнутой АС интегрирующих звеньев.
При исследовании устойчивости считается по известной передаточной функции разомкнутой АС. Заменяем Sна j 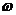и тем самым получаем комплексную передаточную функцию (КПФ). При изменении 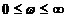вектор КПФ будет вычерчивать кривую – годограф КПФ. По виду этой кривой для разомкнутой АС можно судить о устойчивости замкнутой АС.
Существует 3случая исследования устойчивости по Найквисту:
1 случай: Разомкнутая АС устойчива
2 случай: Разомкнутая АС нейтрально устойчива( на границе устойчивости) и имеет в своем составе 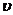интегрирующих звеньев.
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( mкорней характеристического уравнения с положительными вещественными частями.
2 случай: Нейтрально устойчивая АС
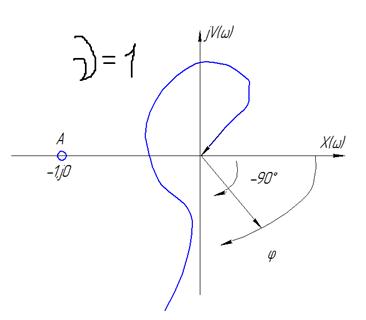ПФ можно представить в виде
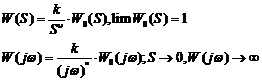
Т.к. годограф КПФ начинается в бесконечности трудно судить охватывает ли годограф КПФ разомкнутой АС критическую точку или нет. Для разрешения этого вопроса введем дугу бесконечного радиуса с угловой координатой омега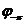 
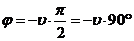
Полученную таким образом дугу назовем дополнением. Для устойчивости замкнутой АС в случае нейтрально устойчивой разомкнутой АС и имеющей 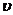интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.
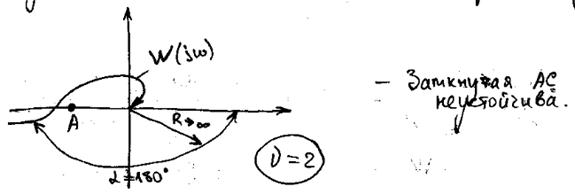
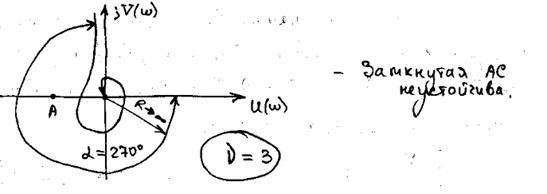
- Частотный критерий устойчивости Найквиста в случае неустойчивой замкнутой АС. Обобщенный критерий устойчивости Цыпкина.
При исследовании устойчивости считается по известной передаточной функции разомкнутой АС. Заменяем Sна j 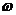и тем самым получаем комплексную передаточную функцию (КПФ). При изменении 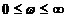вектор КПФ будет вычерчивать кривую – годограф КПФ. По виду этой кривой для разомкнутой АС можно судить о устойчивости замкнутой АС.
Существует 3случая исследования устойчивости по Найквисту:
1 случай: Разомкнутая АС устойчива
2 случай: Разомкнутая АС нейтрально устойчива( на границе устойчивости) и имеет в своем составе 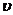интегрирующих звеньев.
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( mкорней характеристического уравнения с положительными вещественными частями.
2 случай: Нейтрально устойчивая АС
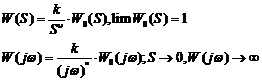
В этом случае трудно судить охватывает ли годограф КПФ разомкнутой АС критическую точку или нет. Для разрешения этого вопроса введем бесконечного радиуса с угловой координатой омега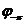
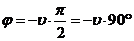
Полученную таким образом дугу назовем дополнением. Для устойчивости замкнутой АС в случае нейтрально устойчивой разомкнутой АС и имеющей 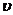интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.
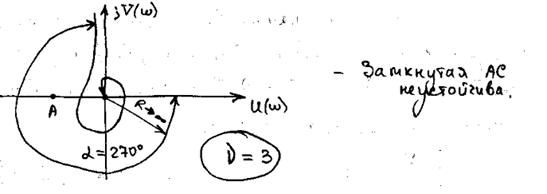
3 случай: Разомкнутая АС неустойчива и имеет m правых полюсов ( mкорней характеристического уравнения с положительными вещественными частями.
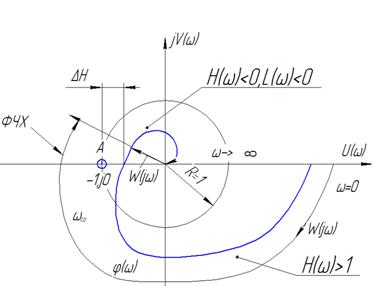
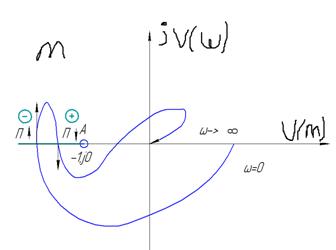В окрестности критической точки в этом случае получается сложная картина поведения годографа разомкнутой АС (петли самопересечения. В этом случае используется обобщенный критерий устойчивости Ципкина.
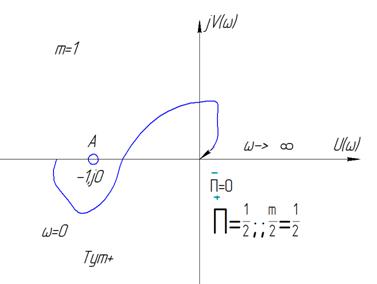
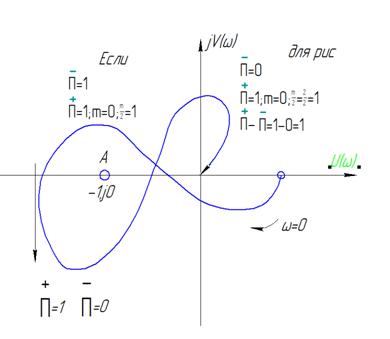Переход годографа КПФ слева от критической точки снизу вверх обознчают «П-» и называют отрицательным переходом, сверху вниз-положительным переходом «П+». Для устойчивости замкнутой АС в случае неустойчивой разомкнутой АС и имеющей в своем составе mправых полюсов (mкорней характеристического уравнения разомкнутой АС) необходимо и достаточно чтобы разность между положительным и отрицательным переходами была равна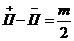 
Если годограф КПФ начинается на отрезке слева от критической точки то переход равен +-1/2. + если вверх,- если вниз идет.
- Логарифмический критерий устойчивости Найквиста. Обобщенный логарифмический критерий устойчивости.
:
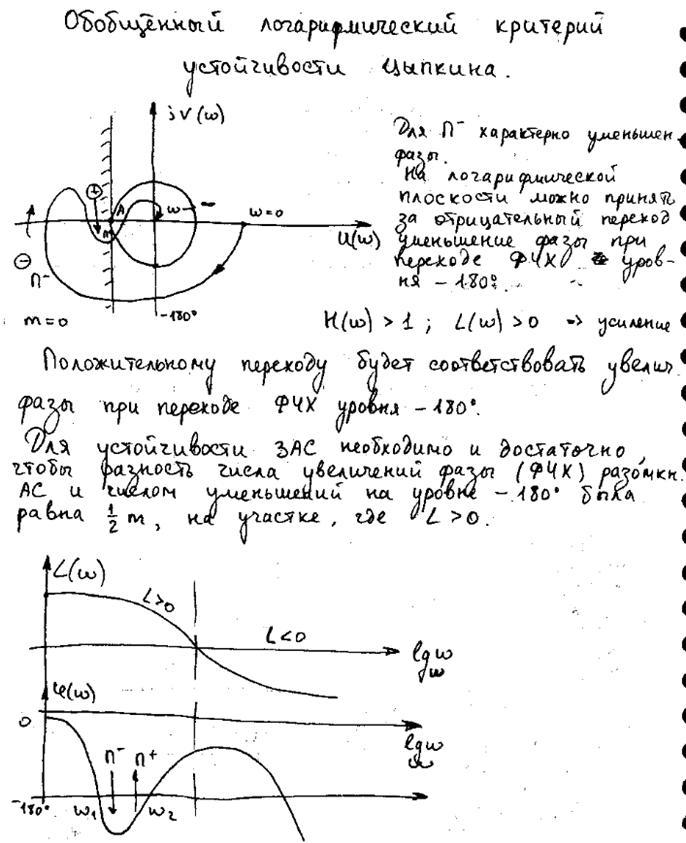
Для устойчивости Замкнутой АС в случае неустойчивой размокнутой АС необходимо и достаточно чтобы разность между числом увеличения ФЧХ и уменьшением ФЧХ на уровне -180 грудосов в области усиления (L>0) была равна m/2
- Понятие о запасах устойчивости. Общепринятые запасы устойчивости (запас по фазе и амплитуде).
Во время работы АС параметры АС изменяются (износ, старение системы). Поэтому необходимо обеспечить не только устойчивость, но и некоторый запас устойчивости, так как АС может находиться близко к границе устойчивости.
Запас устойчивости-степень удаленности АС от границ устойчивости. Запас устойчивости вводится с использованием критерий устойчивости.