Уравнения кривых второго порядка на плоскости: окружость, эллипс, парабола, гипербола

Поверхность, образованная вращением линии вокруг оси, называется поверхностью вращения.

При соответствующем выборе прямоугольной декартовой системы координат в пространстве уравнение поверхности вращения можно привести к одному из видов:

1. Эллипсоид.

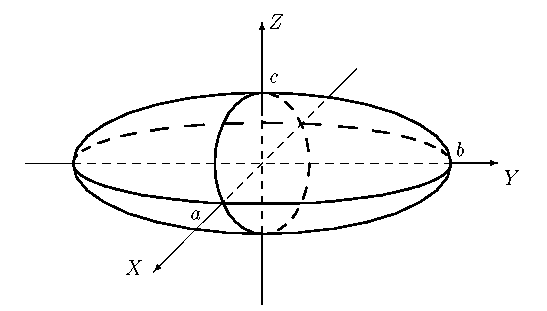
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

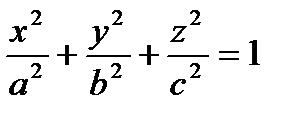
Уравнение 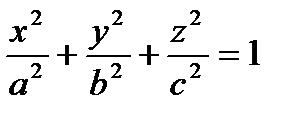называется каноническим уравнением эллипсоида.

Величины 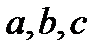- полуоси эллипсоида. Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид является поверхностью вращения. Если , эллипсоид представляет собой сферу.

Поверхност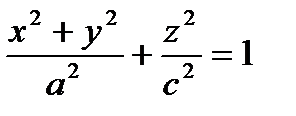и и 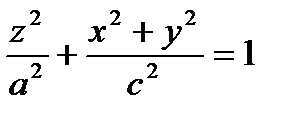называются сжатым и вытянутым эллипсоидами вращения.

y

вытянутый

сжатый

y

z

x

x

z

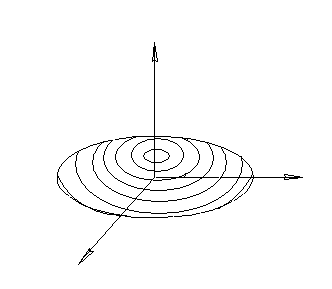
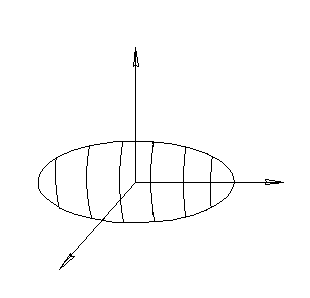
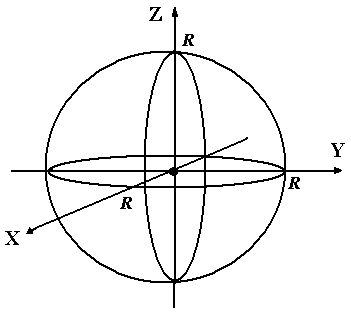
Если 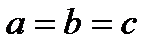, эллипсоид представляет собой сферу с центром в начале координат радиуса R: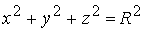

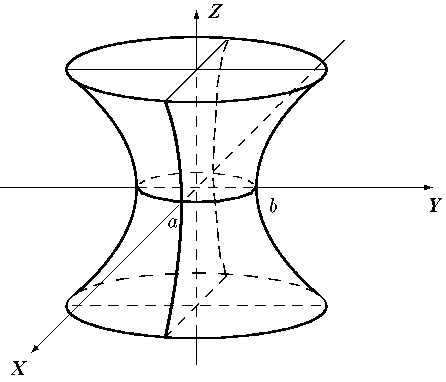
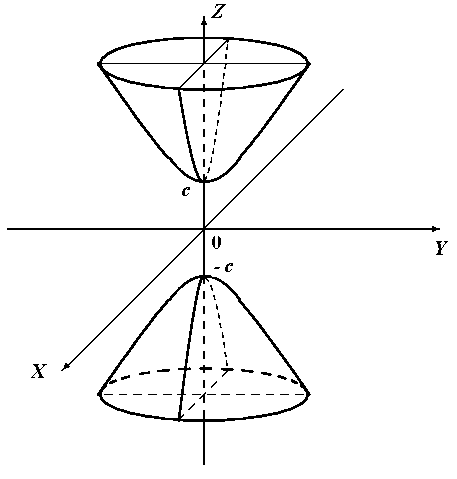
2. Однополосный гиперболоид. Двухполосный гиперболоид.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

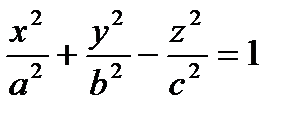
и

.

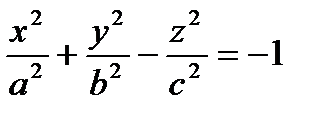Гиперболоид, определяемый уравнением 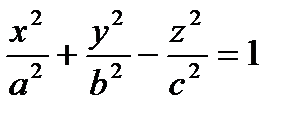, называется однополосным гиперболоидом.

Гиперболоид, определяемый уравнением 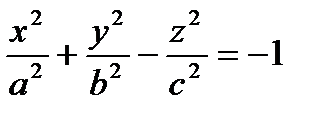, называется двухполосным гиперболоидом.

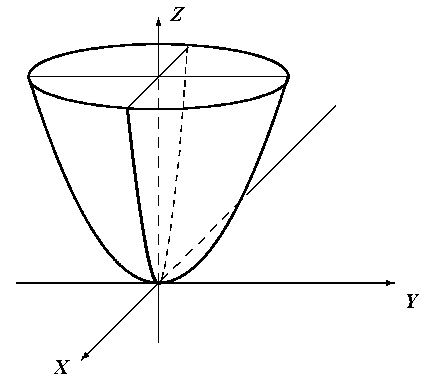
3. Эллиптический параболоид. Гиперболический параболоид.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

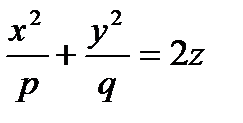
и

,

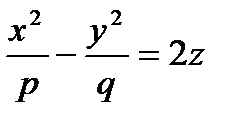где 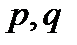- положительные числа, называемые параметрами параболоида.

Параболоид, определяемый уравнением 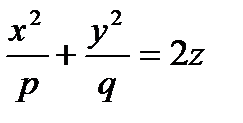, называется эллиптическим параболоидом.

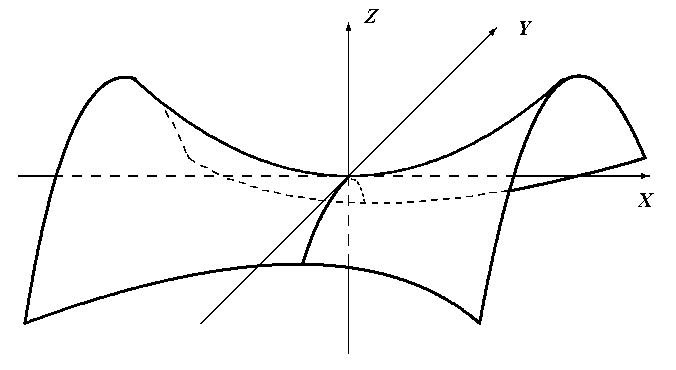
Параболоид, определяемый уравнением 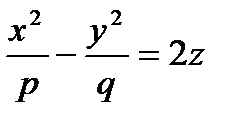, называется гиперболическим параболоидом.

11 Плоскость в пространстве различные формы её задания

12 Уравнение прямой проходящие через 2 точки. Взаимное расположение прямых в пространстве. Угол между 2 прямыми

Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

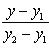
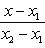
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

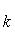
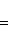
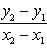
A₁x + B₁y + C₁ = 0

A₂x + B₂y + C₂ = 0

то угол φ между ними вычисляется по формуле:

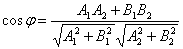(народ в знаменателе вместо б 1 квадрат нужно а 2 квадрат и вместо а 2 квадрат б 1 квадрат)

Или tg(w)=(А1В2-А2В1)\(А1А2+В1В2) –дробью

Условие перпендикулярности этих прямых имеет вид

А1А2+В1В2=0

Условие параллельности

А1\А2=В1\В2≠С1\С2

Пример:

4. Найти угол между двумя прямыми х+у-9=0 и х-6у+5=0

Тангенс фи=(1*(-6)-1*1)\(1*1+1*(-6))=7\5

Фи=арктангенс (7\5)

5. Доказать что прямые 3х-15у+16=0 и 6х-30у+13=0 параллельны

3\6=-15\-30≠16\13 следовательно параллельны

6. 30х+6у+6=0 и 6х-30у+13=0 доказать перпендикулярность

30*6+6*(-30)=0 следовательно перпендикулярны

Условия перпендикулярности и параллельности соблюдаются, т к тождества верны