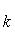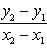Операции над комплексными числами в алгебраической форме
Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов; учитывая при этом, что 
, 
и т. д.
1. Суммой двух комплексных чисел 
называется число 
такое, что справедливы равенства 
, 
, т. е.
. (1.9)
Обозначение: 
.
Правило сложения.При сложении комплексных чисел складываются действительные и мнимые части соответственно
Пример 1.6. Найти сумму чисел 
и 
, где 
, 
.
Решение. 
.
2. Разностью комплексных чисел 
называется число такое, что справедливы равенства 
, 
, т.е.
. (1.10)
Обозначение: 
.
Правило вычитания.При нахождении разности комплексных чисел из действительной и мнимой частей уменьшаемого 
вычитаются соответственно действительная и мнимая части вычитаемого.
Пример 1.7. Найти разность чисел и , где , .
Решение. 
.
3. Произведением чисел называется число такое, что справедливы равенства 
, 
. Обозначение: 
.
Нетрудно убедиться, что эти равенства имеют место, если произвести формальное перемножение выражений 
как двучленов:
(1.11)
Правило умножения.Комплексные числа перемножаются как двучлены, при этом учитывается, что 
.
Пример 1.8.Найти произведение чисел 
и .
Решение.
.
Замечание. 
.
Результат замечания можно сформулировать как свойство: произведение сопряженных комплексных чисел – число действительное.
4. Частнымот деления числа 
( 
) называется число 
, такое, что справедливо равенство 
. Обозначение: 
.
Правило деления.Чтобы разделитьчисло 
( ), следует числитель и знаменатель дроби 
умножить на число 
, сопряженное знаменателю:
. (1.12)
Пример 1.9.Найти частное от деления числа 
на 
.
Решение.
.
Операции над комплексными числами в тригонометрической форме
Пусть
,
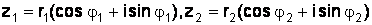тогда
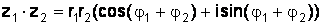; (1.13)
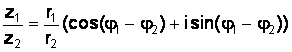. (1.14)
Пример 1.10.Дано: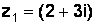 
и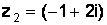 
. Найти произведение 
.
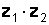Решение.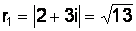 
, 
;
, 
;
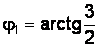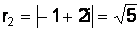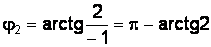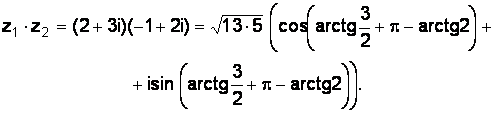
Формула Муавра: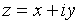 
.
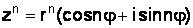; (1.15)
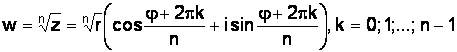; (1.16)
имеет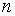 
позиций в области комплексных чисел.
Из формулы (1.16) видно, что все 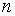различных значений величины 
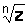имеют один и тот же модуль, равный 
. А так как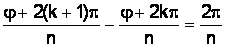 
, то точки, соответствующие значениям 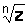, являются вершинами правильного 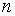-угольника, вписанного в окружность радиуса 
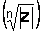, с центром в начале координат.
Пример 1.11.Найти все значения комплексно числа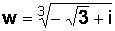 
.
Решение.
; 
; 
.
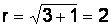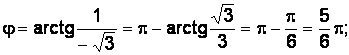
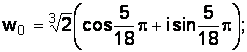
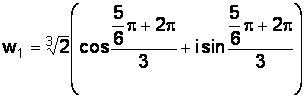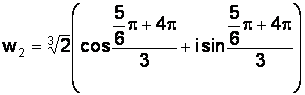Операции над комплексными числами в показательной форме.
Пусть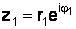 
и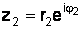 
, тогда
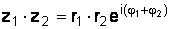; (1.17)
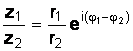; (1.18)
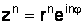; (1.19)
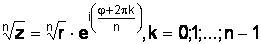. (1.20)
Пример 1.12. Вычислить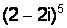 
.
Решение.
; 
;
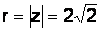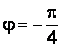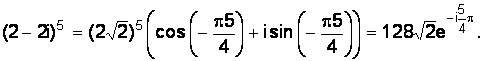
Уравнения прямой проходящей через точку, уравнения прямой проходящей через 2 точки
1. Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k,
y - y1 = k(x - x1).
Это уравнение определяет пучок прямых, проходящих через точку A(x1, y1), которая называется центром пучка.
2. Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:
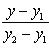
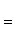
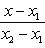
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
