Принцип возможных перемещений

Для равновесия механической системы с идеальными голономными стационарными неосвобождающими связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на систему активных сил на любом возможном перемещении системы из предполагаемого положения равновесия равнялась нулю.

.

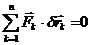Задачи с использованием принципа возможных перемещений рекомендуется решать в следующей последовательности:

1) построить схему механической системы с приложенными к ней внешними активными силами (при наличии неидеальных связей их отбросить и заменить соответствующими реакциями);

2) при необходимости определить реакцию связи мысленно от­бросить связи и заменить ее реакцией;

3) определить независимые возможные перемещения точек си­стемы (их число равно числу степеней свободы системы);

4) дать системе возможное перемещение, соответствующее одной из степеней свободы, считая при этом возможные переме­щения, соответствующие остальным степеням свободы, равными нулю; выразить возможные перемещения точек приложения сил через это возможное перемещение;

5) вычислить сумму работ всех сил, указанных в пп. 1) и 2), на соответствующих возможных перемещениях их точек приложе­ния и приравнять эту сумму нулю;

6) последовательно производя выкладки пп. 2) и 5) для каж­дого из независимых возможных перемещений, составить систему уравнений равновесия в числе, равном числу степеней свободы системы;

7) решив полученную систему уравнений, найти искомые ве­личины.

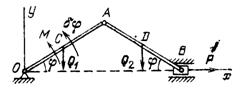Пример 1. На кривошип ОА кривошипно-ползунного меха­низма, расположенного в вертикальной плоскости (рис. 556), дей­ствует пара сил с моментом М. Кривошип и шатун равной длиныОА = АВ = l представ­ляют собой однородные стержни весом Q₁ и Q₂ соответ­ственно, вес ползуна В ра­вен Q₃, положение механизма задано на чертеже. Пренебрегая трением, найти горизонтальную силу Р, приложен­ную к ползуну и удерживающую механизм в равновесии.

Решение. К системе приложены активные силы

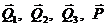и момент M.

Рис. 556 Положение механизма определяется углом φ, т. е. си­стема имеет одну степень свобо-ды и мы можем ей дать одно незави­симое возможное переме-щение, увеличив угол φ на величину δφ. В силу принципа возможных перемещений

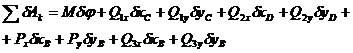
Так как Q_1x = 0, Q_1y = -Q₁, Q_2x = 0, Q_2y = -Q₂, P_x = Р, Р_у = 0, δу_B= 0, Q_3х = 0, то

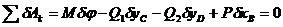
Найдем соотношение между проекциями возможных перемещений различных точек и δφ. Из схемы видно, что

y_C = у_D = (l/2) sin φ, х_B = 2l cos φ.

Дифференцируя эти соотношения, находим

δу_C = δу_D = (l/2) cos φδφ, δх_B = - 2lsinφδφ.

Подставим полученные значения в исходное уравнение:

Mδφ – (Q₁+Q₂)(l/2) cos φδφ - 2Plsinφδφ = 0.

В записанных ниже выражениях символ δ (вместо d) оз­начает, что получаются возможные, а не действительные переме­щения. Строго говоря, здесь производится операция не дифферен­цирования, а варьирования, т. е. дифференцирования при фикси­рованном времени. Откуда

.

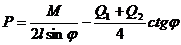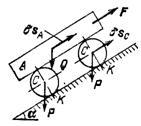Пример 2. Вес бревна А (рис. 557) равен Q, вес каждого из цилиндрических катков, на которые оно положено, равен Р. Катки катятся по наклонной плоскос-ти (угол α задан) без скольжения, бревно по каткам не скользит. Какую силу 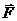, параллельную линии наибольшего ската, надо прило­жить к бревну, чтобы удержать его в рав­новесии?

Решение. Так как скольжение от-­

Рис. 557 сутствует, связи, наложенные на систе-му, являются идеальными. Сообщив системе возможное пере-мещение δs_A и вычислив возможные работы приложенных к сист Fδs_A еме активных сил ( 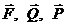), получим

Fδs_A – Q sin α δs_A – 2P sin α δs_C = 0

Так как точка К является мгновенным центром скоростей катков, то δs_A = 2δs_C, откуда

2Fδs_C – 2Q sin α δs_C – 2P sin α δs_C = 0

или F = (P + Q) sin α .

Задачи