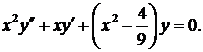Интегрирование дифференциальных уравнений с помощью рядов

1. Применение рядов к решению дифференциальных уравнений. В некото­рых случаях, когда интегрирование дифференциального уравнения в элемен­тарных функциях невозможно, решение такого уравнения ищут в виде степен­ного ряда

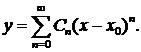
Неопределенные коэффициенты 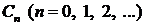находят подстановкой ряда в уравнение и приравниванием коэффициентов при одинаковых степенях разности 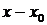в обеих частях полученного равенства. Если удается найти все коэффициенты ряда, то полученный ряд определяет решение во всей своей

области сходимости.

В тех случаях, когда длу уравнения 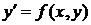требуется решить задачу Коши при начальном условии 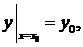решение можно искать с помощью ряда Тейлора:

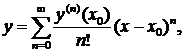
где 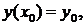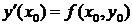, а дальнейшие производные 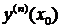находят последовательным дифференцированием исходного уравнения и подстановкой в результат дифференцирования вместо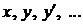значений 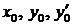и всех остальных найденных последующих производных. Аналогично с помощью ряда Тейлора можно интегрировать и уравнения высших порядков.

756. Проинтегрировать уравнение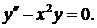

Δ Будем искать решение этого уравнения в виде ряда

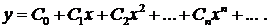
Подставляя у и у" в исходное уравнение, находим

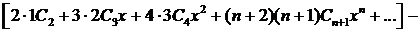
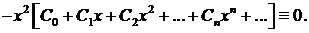
Сгруппируем члены с одинаковыми степенямих:

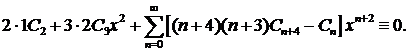
Приравнивая нулю все коэффициенты полученного ряда (чтобы уравнение об­ратилось в тождество), находим

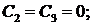
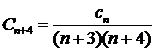
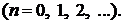
Последнее соотношение позволяет найти последовательно все коэффициенты искомого разложения (Со и С₁ остаются произвольными и играют роль про­извольных постоянных интегрирования);

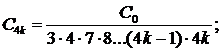
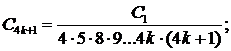
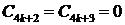
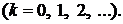
Таким образом,

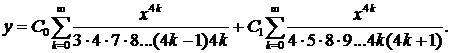
Полученные ряды сходятся на всей числовой оси и определяют два линей­но независимых частных решения исходного уравнения. ▲

С помощью разложения в ряд по степеням х проинтегрировать следующие уравнения н определить область существования полу­ченного решения:

757.

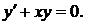
758.

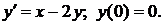
ф В силу начального условия положить Со==0.

759. у"+ху'+у=0.

760. у"—ху'—2у=0.

761.

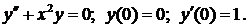
● В силу начальных условий положить Со=0, С₁=1.

762. Проинтегрировать приближенно с помощью ряда Тейло­ра уравнение 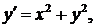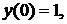взяв шесть первых членов разложения, отличных от нуля.

Δ Из уравнения начальных условий находим 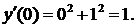Диффе­ренцируя данное уравнение, последовательно получаем

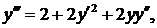
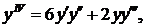
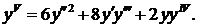
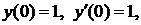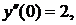
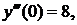
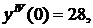
Полагаях=0 и используя значения последовательно нахо­дим 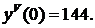Искомое решение имеет вид

▲

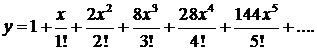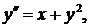
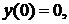
763. 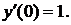Найти четыре первых (отличных от нуля) члена разложения.

. Δ Дифференцируя уравнение 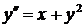имеем

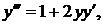
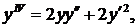
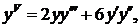
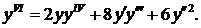
При х=0 получаем

у(0)=0, у'(0)=1,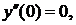

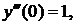
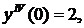
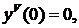
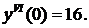
Решение имеет вид

▲

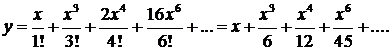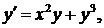
764. 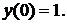Найти четыре первых (отличных от нуля) члена разложения.

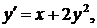
765. 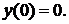Найти два первых (отличных от нуля) члена разложения.

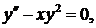
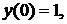
766. 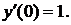Найти четыре первых (от­личных от нуля) члена разложения.

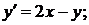
767. 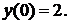Найти точное решение.

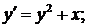
768. 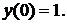Найти пять первых членов разложения.

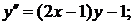
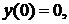
769. 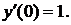Найти пять первых членов разложения.

2. Уравнение Бесселя. Линейное дифференциальное уравнение с переменны­ми коэффициентами, имеющее вид

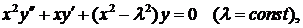(1)

называется уравнением Бесселя (к этому же виду сводится уравнение 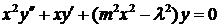заменой ),

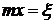Решение уравнения (1) будем искать в виде обобщенного степенного ряда, т. е. произведения некоторой степени х на степенной ряд:

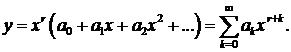(2)

Подставляя обобщенный степенной ряд в уравнение (1) и приравнивая нулю коэффициенты при каждой степени х в левой части уравнения, получим систему

ФОРМУЛА………………….

Считая, что 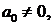из данной системы находим 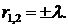Пусть 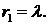Тогда из второго уравнения системы находим 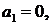а из уравнения 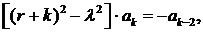придавая k значения 3, 5, 7, ... , заключаем, что 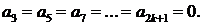Дяя коэффициентов с четными номерами получаем вы­ражения

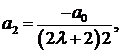
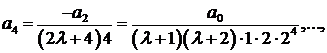
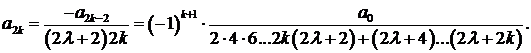
Подставляя найденные коэффициенты в ряд (2), получим решение

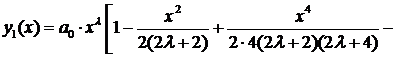
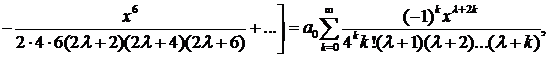
где коэффициент 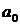остается произвольным.

При 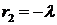все коэффициенты ад аналогично определяются только в слу­чае, когда 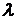не равно целому числу. Тогда решение можно получить, заменяя в предыдущем решении 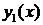величину 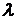на — :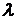

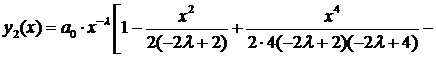
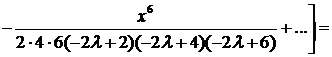
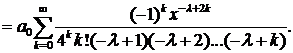
Полученные степенные ряды сходятся для всех значений х, что легко устанав­ливается на основании признака Даламбера. Решения у₁ (х) и y₂(х) линейно независимы, так как их отношение не является постоянным.

Решение у₁(х), умноженное на постоянную 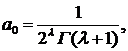называется функцией Бесселя (или цилиндрической функцией) порядка λ первого рода и обозначается символом 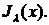Решение у₂ обозначают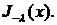

Следовательно, общее решение уравнения (1) при λ, не равном целому чгслу, имеет вид

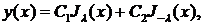
где C₁ и С₂—произвольные постоянные величины.

В общепринятом выборе постоянной 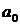участвует гамма-функция 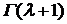, которая определяется несобственным интегралом (см. с. 35):

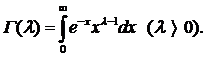
Можно показать, что при λ, равном половине нечетного числа, функция Бссселя выражается через элементарные функции, так как в этом случае гам­ма-функция, входящая в определение функции Бесселя

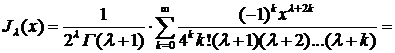
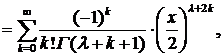
[произведение 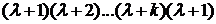заменено, согласно свойству гамма-функции, на 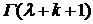], принимает следующие значения:

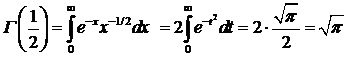
(здесь использовано значение интеграла Пуассона);

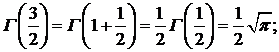
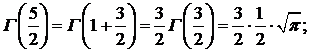
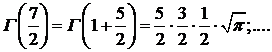
Функцию Бесселя 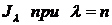(натуральном) можно записать так:

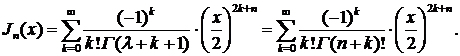
Для отрицательного и целого λ частное решение не выражается функцией Бесселя первого рода и его следует искать в форме

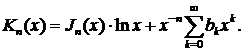
Подставляя это выражение в уравнение (1), мы определим коэффициенты 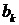. Функция 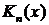умноженная на некоторую постоянную, называется функ-цией Бесселя п-го порядка второго рода.

770. Найти функцию Бесселя при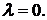

Δ Воспользовавшись равенством

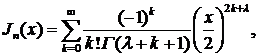
при 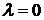получим

▲

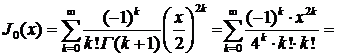
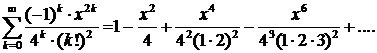771. Решить уравнение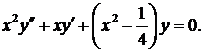

Δ Так как 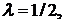то общее решение уравнения имеет вид 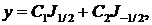где

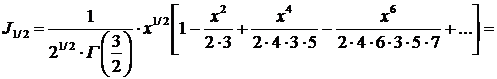
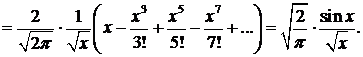
Точно так же получим 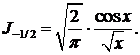Следовательно, общее решение

▲

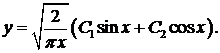772. Найти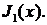

773. Решить уравнение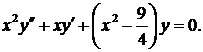

774. Решить уравнение