Определитель квадратной матрицы
Определитель матрицы обозначается стандартным математическим символом |A|. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) или набрать на клавиатуре <|> (нажав клавиши <Shift>+<\>). В результате появляется местозаполнитель, в который следует поместить матрицу. Чтобы вычислить определитель уже введенной матрицы, нужно:
1. Переместить курсор в документе таким образом, чтобы поместить матрицу между линиями ввода.
2. Ввести оператор нахождения определителя матрицы.
3. Ввести знак равенства, чтобы вычислить определитель.
Обратная матрица
Поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Inverse (Обратная матрица) на панели инструментов Matrix (Матрица).
Решение матричных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x1, x2,…,xn.
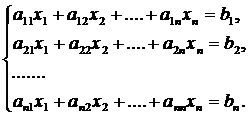 (1)
(1)
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в виде: 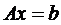 , где:
, где:
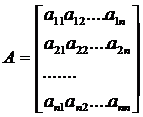
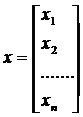
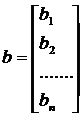
Если определитель матрицы А не равен 0, то система имеет единственное решение, т.к. существует обратная матрица А-1 при умножении обеих частей уравнения на которую получаем:
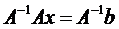
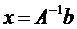
Системы линейных уравнений удобно решать с помощью функции lsolve:
lsolve(А, b)-возвращается вектор решения x такой, что 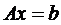 (см. рис. 9).
(см. рис. 9).
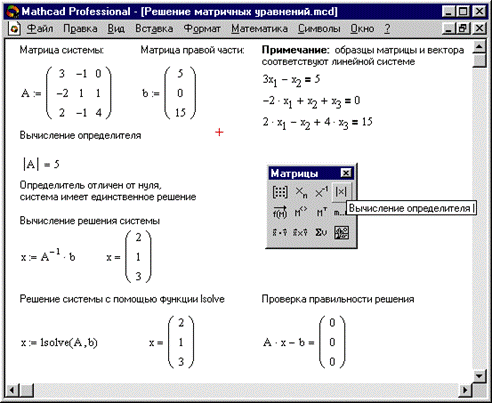
Рис.9.
Метод Гаусса
Метод Гаусса состоит в том, что систему (1) приводят последовательным исключение неизвестных к эквивалентной системе с треугольной матрицей:
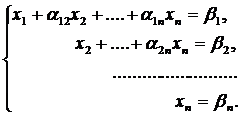
решение которой находят по рекуррентным формулам:
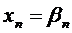 ,
, 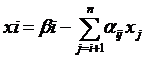
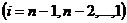
В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:
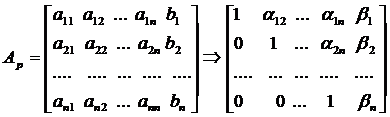
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:
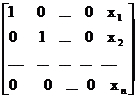
Последний, (n+1) этой матрицы содержит решение системы (1).
В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A). На рис.10 показано решение системы линейных уравнений методом Гаусса, в котором используются следующие показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции:
rref(A)- возвращает ступенчатую форму матрицы А.
augment(A, В) - возвращает матрицу, сформированную слиянием матриц-аргументов слева направо. Массивы Aи В должны иметь одинаковое число строк.
submatrix(A, ir, jr, ic, jc) - возвращает матрицу, состоящую из всех элементов с ir по jr строки столбцах с ic по jc. Удостоверьтесь, что ir ≤jr и ic ≤jc, иначе порядок строк и (или) столбцов будет обращен.
 Рис. 10
Рис. 10
Создание графиков
В Mathcad встроено несколько различных типов графиков, которые можно разбить на две большие группы:
Ø Двумерные графики
- XY (декартовый) график,
- полярный график;
Ø Трехмерные графики
- график трехмерной поверхности,
- график линий уровня,
- трехмерная гистограмма,
- трехмерное множество точек,
- векторное поле.
Чтобы создать график, например двумерный декартовый, необходимо:
1) Поместить курсор ввода в то место, куда требуется вставить график.
2) Нажмите на панели Graph (График) кнопку X-Y Plot для создания Декартового графика.
3) В результате в обозначенном месте документа появится пустая область графика с местозаполнителями, в один из которых нужно ввести функцию, а имя аргумента в другой.
В результате Mathcad создает график функции в пределах значений аргумента, по умолчанию принятых равными от –10 до 10.
1.4 Контрольные вопросы
1. Назначение Mathcad
2. Запуск Mathcad
3. Основные элементы окна Mathcad
4. Назначение меню Mathcad
5. Назначение панели инструментов Mathcad
6. Назначение панели форматирования Mathcad
7. Назначение математической панели Mathcad
8. Ввод, редактирование и вычисление выражений
9. Использование переменных в Mathcad
10. Создание и использование собственных функций пользователя
11. Переменные с заданным диапазоном изменения значений и переменные с индексами
12. Построение графиков функций
13. Ввод и форматирование текста
14. Копирование, перемещение, удаление фрагментов документа.
15. Использование Буфера Обмена при редактировании документа.
16. Сохранение и загрузка документа.
17. Просмотри печать документа
18. Численное дифференцирование и интегрирование функций.
19. Решение уравнений
20. Символьное дифференцирование и интегрирование функций.
21. Вставка результатов вычислений Mathcad в документ Word.
Домашнее задание № 2
«Основы работы в MatLab»
Введение
Пакет MatLab был создан компанией MathWorks. MatLab является мощным и универсальным средством решения задач, возникающих в различных областях человеческой деятельности. Спектр проблем, исследование которых может быть осуществлено при помощи MatLab, охватывает:
Ø матричный анализ;
Ø обработку сигналов и изображений;
Ø задачи математической физики;
Ø оптимизационные задачи;
Ø обработку и визуализацию данных;
Ø работу с картографическими изображениями;
Ø нейронные сети, нечеткую логику и многие другие.
Специализированные средства собраны в пакеты, называемые ToolBox, и могут быть выборочно установлены вместе с MatLab по желанию пользователя. В состав многих ToolBox входят приложения с графическим интерфейсом пользователя, которые обеспечивают быстрый и наглядный доступ к основным функциям. Пакет Simulink, поставляемый вместе с MatLab, предназначен для интерактивного моделирования нелинейных динамических систем, состоящих из стандартных блоков.
MatLab прекрасно интегрируется с Microsoft Word и Excel. Связь MatLab и Word обеспечивает возможность написания в редакторе Word интерактивных документов, так называемых М-книг, основанных на специальном шаблоне. Пользователь, работающий с М-книгой, может запускать блоки команд MatLab непосредственно из документа Word, причем результат выполнения команд отображается в М-книге. Данное средство прекрасно подходит для создания отчетов и учебных пособий, поскольку позволяет дополнить документ примерами и результатами расчетов.
Надстройка Excel Link, поставляемая вместе с MatLab, существенно расширяет возможности Excel, обеспечивая доступ пользователя к функциям MatLab и ToolBox. Подготовка данных осуществляется непосредственно в электронных таблицах, а обращение к функциям производится либо из ячеек рабочего листа, либо в модуле, написанном на Visual Basic.
2.1 Цели и задачи домашнего задания
Познакомиться с пакетом MatLab, принципами его работы, научиться выполнять простейшие вычисления в MatLab.
2.2 Содержания домашнего задания
Вариант задания каждого студента соответствует его порядковому номеру по списку в журнале.
Описать порядок действий (команд), произведенных при решения каждого задания.
Задание 2.2.1
Вычислить с различной точностью:
1. 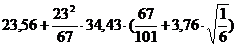
2. 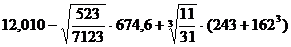
3. 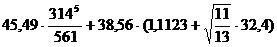
4. 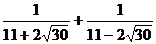
5. 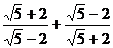
6. 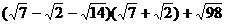
7. 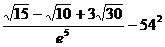
8. 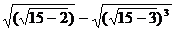
9. 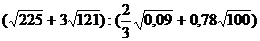
10. 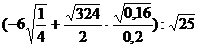
11. 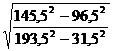
12. 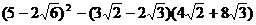
13. 
14. 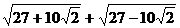
15. 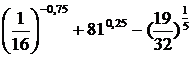
16. 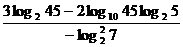
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 2.2.2
Вычислите значения следующих выражений, используя окно Command History:
1. 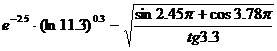 ;
; 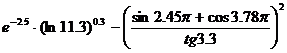
2. 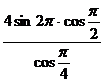 ;
; 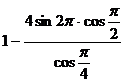
3. 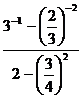 ;
; 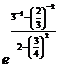
4. 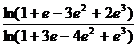 ;
; 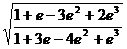
5. 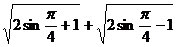 ;
; 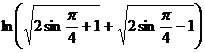
6. 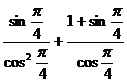 ;
; 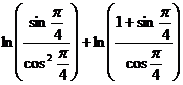
7. 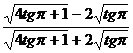 ;
; 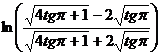
8. 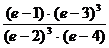 ;
; 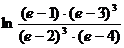
9. 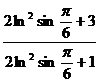 ;
; 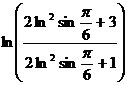
10. 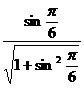 ;
; 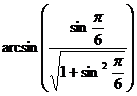
11. 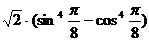 ;
; 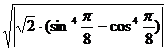
12. 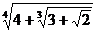 ;
; 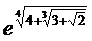
13. 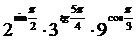 ;
; 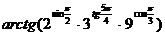
14. 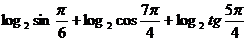 ;
; 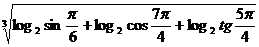
15. 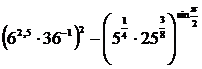 ;
; 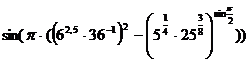
16. 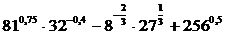 ;
; 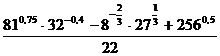
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 2.2.3
Найдите значения следующих выражений, используя переменные:
1. 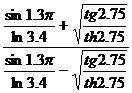
2. 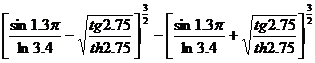
3. 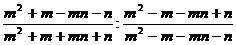 при m=5, n=3
при m=5, n=3
4. 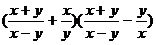 при x=4, y=5
при x=4, y=5
5. 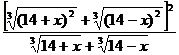 при x=25
при x=25
6. 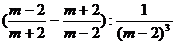 при m=8
при m=8
7. 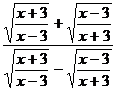 при x=2
при x=2
8. 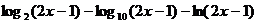 при x=8
при x=8
9. 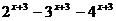 при x=1
при x=1
10. 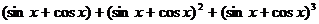 при x= π/4
при x= π/4
11. 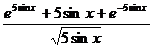 при x= π/4
при x= π/4
12. 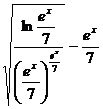 при x=3
при x=3
13. 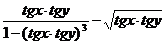 при
при 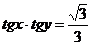
14. 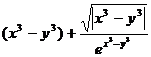 при x=3, y=5
при x=3, y=5
15. 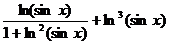 при x= π/6
при x= π/6
16. 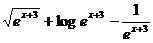 при x=5
при x=5
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 2.2.4
Найти сумму матриц
1. 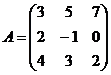 и
и 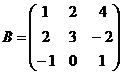 2.
2. 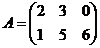 и
и 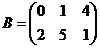
3. 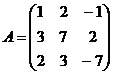 и
и 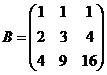 4.
4. 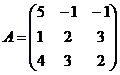 и
и 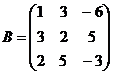
5. 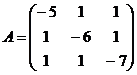 и
и 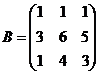 6.
6. 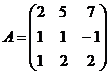 и
и 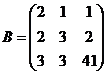
7. 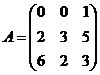 и
и 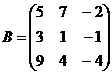 8.
8. 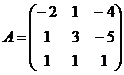 и
и 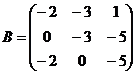
9. 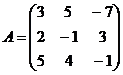 и
и 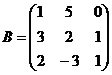 10.
10. 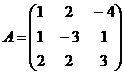 и
и 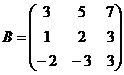
11. 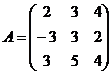 и
и 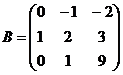 12.
12. 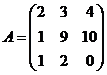 и
и 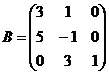
13. 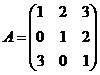 и
и 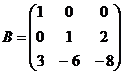 14.
14. 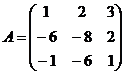 и
и 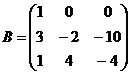
15. 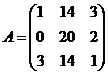 и
и 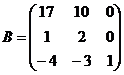 16.
16. 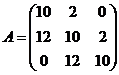 и
и 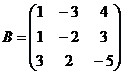
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________
Задание 2.2.5
Дана матрица А. Вычислить определитель матрицы А и найти транспонированную матрицу.
1. 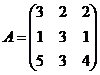 2.
2. 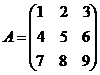 3.
3. 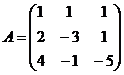
17. 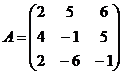 5.
5. 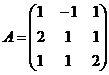 6.
6. 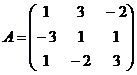
7. 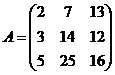 8.
8. 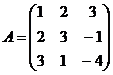 9.
9. 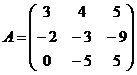
10. 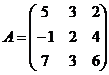 11.
11. 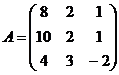 12.
12. 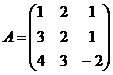
13. 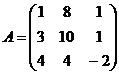 14.
14. 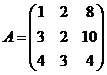 15.
15. 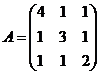
16. 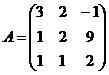
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________
Задание 2.2.6
Выведите таблицу значений функции
1. 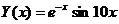 на отрезке [0,1] с шагом 0.05.
на отрезке [0,1] с шагом 0.05.
2. 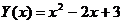 на отрезке [-11,1] с шагом 1.
на отрезке [-11,1] с шагом 1.
3. 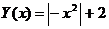 на отрезке [-2,3] с шагом 0.5.
на отрезке [-2,3] с шагом 0.5.
4. 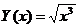 на отрезке [5,6] с шагом 0.02.
на отрезке [5,6] с шагом 0.02.
5. 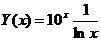 на отрезке [2,4] с шагом 0.1.
на отрезке [2,4] с шагом 0.1.
6. 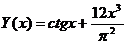 на отрезке [3,5] с шагом 0.2.
на отрезке [3,5] с шагом 0.2.
7. 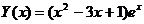 на отрезке [-2,-1] с шагом 0.1.
на отрезке [-2,-1] с шагом 0.1.
8. 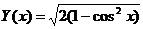 на отрезке [0, π] с шагом π/6.
на отрезке [0, π] с шагом π/6.
9. 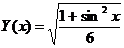 на отрезке [0, 2π] с шагом π/4.
на отрезке [0, 2π] с шагом π/4.
10. 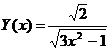 на отрезке [5,7] с шагом 0.5.
на отрезке [5,7] с шагом 0.5.
11. 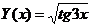 на отрезке [0, π/2] с шагом π/12.
на отрезке [0, π/2] с шагом π/12.
12. 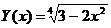 на отрезке [-1,1] с шагом 0.05.
на отрезке [-1,1] с шагом 0.05.
13. 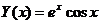 на отрезке [-2,3] с шагом 0.03.
на отрезке [-2,3] с шагом 0.03.
14. 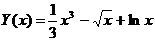 на отрезке [7,10] с шагом 0.4.
на отрезке [7,10] с шагом 0.4.
15. 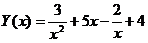 на отрезке [3,5] с шагом 0.05.
на отрезке [3,5] с шагом 0.05.
16. 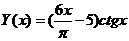 на отрезке [π, 2π] с шагом π/2 .
на отрезке [π, 2π] с шагом π/2 .
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________
Задание 2.2.7
Постройте графики функций:
1. 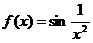 и
и 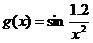 на отрезке [-1, -0.3]
на отрезке [-1, -0.3]
2. 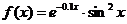 и
и 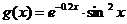 на отрезке [-2p; 2p]
на отрезке [-2p; 2p]
3. 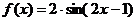 и
и 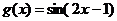 на отрезке [0; 2p] с шагом p/24
на отрезке [0; 2p] с шагом p/24
4. 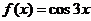 и
и 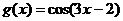 на отрезке [-2p; p]
на отрезке [-2p; p]
5. 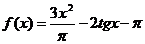 и
и 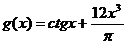 на отрезке [p/6; 2p] с шагом p/512
на отрезке [p/6; 2p] с шагом p/512
6. 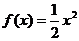 и
и 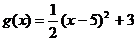 на отрезке [-10;15]
на отрезке [-10;15]
7. 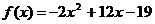 и
и 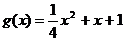 на отрезке [-8;8]
на отрезке [-8;8]
8. 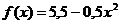 и
и 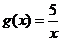 на отрезке [0,05;10]
на отрезке [0,05;10]
9. 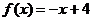 и
и 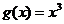 на отрезке [-4;4]
на отрезке [-4;4]
10. 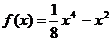 и
и 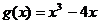 на отрезке [-3;3]
на отрезке [-3;3]
11. 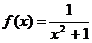 и
и 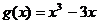 на отрезке [-5;5]
на отрезке [-5;5]
12. 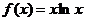 и
и 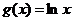 на отрезке [0,1;12]
на отрезке [0,1;12]
13. 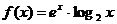 и
и 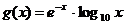 на отрезке [0,2;3]
на отрезке [0,2;3]
14. 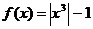 и
и 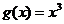 на отрезке [-3;3]
на отрезке [-3;3]
15. 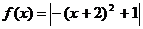 и
и 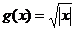 на отрезке [-5;0]
на отрезке [-5;0]
16. 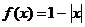 и
и 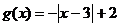 на отрезке [-5;5]
на отрезке [-5;5]
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________
 |
Задание 2.2.8
Постройте график функции:
1. 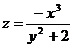
2. 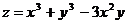
3. 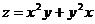
4. 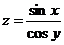
5. 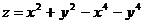
6. 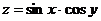
7. 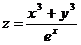
8. 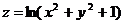
9. 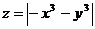
10. 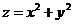
11. 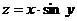
12. 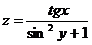
13. 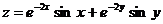
14. 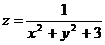
15. 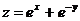
16. 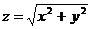
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________
 |
Задание 2.2.9
Найдите все корни полинома
1. 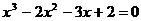
2. 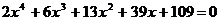
3. 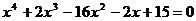
4. 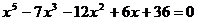
5. 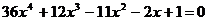
6. 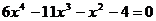
7. 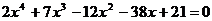
8. 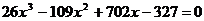
9. 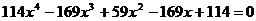
10. 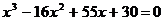
11. 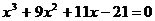
12. 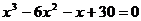
13. 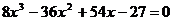
14. 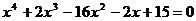
15. 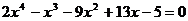
16. 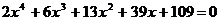
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________
2.3. Порядок выполнения домашнего задания
Рабочая среда MatLab
Запуск MatLab 6.x приводит к открытию рабочей среды, изображенной на рис.1.
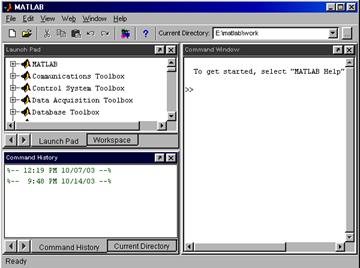
Если в рабочей среде MatLab 6.x отсутствуют некоторые окна, приведенные на рис. 1, то следует в меню Viewвыбрать соответствующие пункты: Command Window, Command History, Current Directory, Workspace, Launch Pad.
Рис.1.Рабочая среда MatLab 6.x
Рабочая среда MatLab 6.хследующие элементы:
· меню;
· панель инструментов с кнопками и раскрывающимся списком;
· окно с вкладками Launch Pad и Workspace,из которого можно получить простой доступ к различным модулям ToolBox и к содержимому рабочей среды;
· окно с вкладками Command History и Current Directory,предназначенное для просмотра и повторного вызова ранее введенных команд, а также для установки текущего каталога;
· командное окно Command Windows;
· строку состояния.
Простейшие вычисления
Встроенные математические функции MatLab позволяют находить значения различных выражений.
Наберите в командной строке 1+2 и нажмите <Enter>. В результате в командном окне MatLab отображается следующее:
>> 1 + 2
ans =
>> |
т.е. программа MatLab вычислила сумму 1+2, затем записала результат в специальную переменную ans и вывела ее значение, равное 3, в командное окно. Ниже ответа расположена командная строка с мигающим курсором, обозначающая, что MatLab готова к дальнейшим вычислениям. Можно набирать в командной строке новые выражения и находить их значения.
Если требуется продолжить работу с предыдущим выражением, например, вычислить (1+2)/4.5, то проще всего воспользоваться уже имеющимся результатом, который хранится в переменной ans. Наберите в командной строке ans/4.5 (при вводе десятичных дробей используется точка) и нажмите <Enter>, получается:
>> ans/4.5
ans=
0.6667
>> |
Вид, в котором выводится результат вычислений, зависит от формата вывода, установленного в MatLab. Далее объяснено, как задать основные форматы вывода.
