Тема: Законы распределения случайных величин.
Цели работы: Познакомиться с понятием случайная величина, законами ее распределения, научиться находить математическое ожидание и дисперсию.
Краткое изложение темы.
Случайная величина – это такая переменная, которая свои значения принимает с определенной вероятностью.
Совокупность значений случайной величины и соответствующих им вероятностей называется распределениемслучайной величины.
Дискретной случайной величиной называется случайная величина, которая принимает отдельные, изолированные друг от друга значения.
Распределение дискретной случайной величины может быть задано графически или таблицей.
Таблица или закон распределения обычно имеет вид
 |  |  | … |  | … |  |
 |  |  | … |  | … |  |
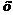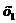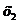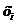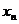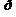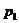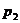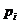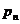Для вероятностей 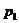, …, 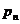справедливо равенство 
.
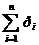Графическим изображением распределения дискретной случайной величины служит совокупность точек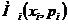 
.
Математическим ожиданием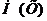 
называется сумма произведений всех возможных значений случайной величины на соответствующие им вероятности:
.
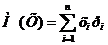Дисперсией случайной величины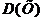 
называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания
.
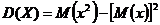Распределение, заданное таблицей
| … |  | … |  | ||
 |  | … |  | … |  |
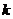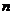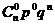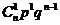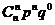где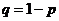 
, называется биноминальным распределением.
Математическое ожидание случайной величины, распределенной по биноминальному закону, равно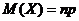 
, а дисперсия равна 
.
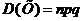Примеры выполнения заданий.
Пример 1. Установить, может ли распределение случайной величины быть задано таблицей:
| 5/2 | е | П | -2/3 | |
| 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Решение:
Поскольку 0,1+0,2+0,3+0,3+0,1=1 и все числа в нижней строке таблицы положительны, то таблица задает закон распределения некоторой случайной величины.
Ответ: да.
Пример 2. Стрелок произвел 150 выстрелов по мишени. Вероятность попадания при каждом выстреле равна 0,9. Найти математическое ожидание и дисперсию числа попаданий.
Решение:
Число попаданий в мишень распределено по биноминальному закону при n=150 и Р=0,9. тогда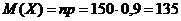 
, 
.
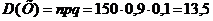Ответ: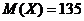 
, 
.
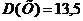Пример 3. Монету бросают два раза. Составить таблицу распределения числа появлений герба и построить график этого распределения. Найти математическое ожидание и дисперсию данной случайной величины.
Решение:
Х – число появлений герба при двукратном бросании монеты, которое может принимать значения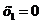 
, 
, 
.
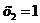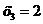А – событие, состоящее в появлении герба.
Тогда
,
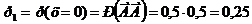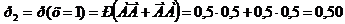
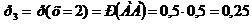
Закон распределения:
| х | |||
| р | 0,25 | 0,5 | 0,25 |
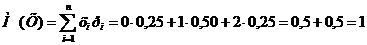
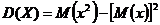
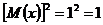
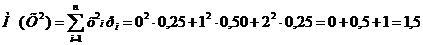
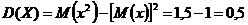
Ответ: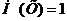 
, 
.
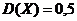| х | |||
| р | 0,25 | 0,5 | 0,25 |
Задания для практической работы.
Вариант 1.
1. Установите, задает ли закон распределения какой-либо случайной величины следующая таблица:
| -1 | |||
 |  |  | |
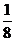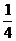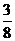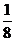2. Охотник сделал 10 выстрелов. Вероятность попадания при одном выстреле 0,7.Определить числовые характеристики распределения числа попаданий.
3. Два шахматиста, играющие в одинаковую силу, сыграли матч из шести партий (ничьих в матче не было). Пусть Х – число партий, выигранных одним из шахматистов. Найдите: а) закон распределения, б) постройте график распределения, в) 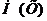, г) .
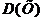Вариант 2.
1. Установите, задает ли закон распределения какой-либо случайной величины следующая таблица:
| -2 | -1 | ||
 | | |
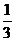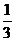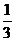2. Доля брака в некоторой продукции составляет 5%. Произведена выборка с возвращением каждый раз отобранного экземпляра. Всего отобрано 100 экземпляров. Определить числовые характеристики распределения количества брака в произведенной выборке.
3. Из урны, содержащей 5 белых и 5 черных шаров, вынимают наудачу три шара. Пусть Х – число вынутых черных шаров. Найдите: а) закон распределения, б) постройте график распределения, в) 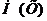, г) .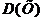
Практическая работа № 10.