Тема: Дифференциальные уравнения второго порядка.
Цели работы: научиться находить общее и частное решения дифференциальных уравнений второго порядка.
Краткое изложение темы.
Уравнение, содержащее производные не выше второго порядка, называется дифференциальным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом:
.
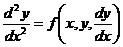Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
,
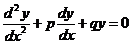где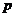 
и 
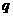- постоянные величины.
Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
- Записать дифференциальное уравнение в виде
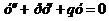. - Составить его характеристическое уравнение:
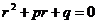(если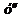 
обозначить через 
, 
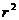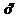- через 
, 
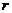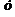- через 1). - Вычислить дискриминант
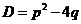; при этом если:
а)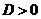 
, то характеристическое уравнение имеет два разных корня 
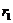и 
.
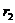Общее решение дифференциального уравнения выражается в виде
,
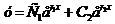где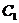 
и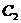 
- произвольные постоянные.
б)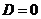 
, то при этом характеристическое уравнение имеет два равных корня = .
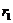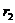Общее решение дифференциального уравнения выражается в виде
,
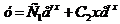где 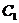и 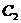- произвольные постоянные.
в)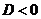 
, то при этом характеристическое уравнение имеет комплексные корни 
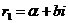и 
.
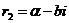Общее решение дифференциального уравнения выражается в виде
,
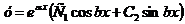где 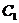и 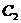- произвольные постоянные.
Примеры выполнения заданий.
Пример 1. Решить уравнение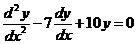 
.
Решение:
Составим характеристическое уравнение:
.
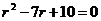Найдем корни данного уравнения:
.
,
.
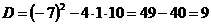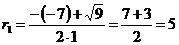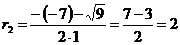Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения запишется так:
.
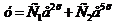Ответ: .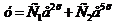
Пример 2. Решить уравнение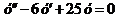 
.
Решение:
Составим характеристическое уравнение:
.
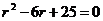Найдем его корни:
.
,
.
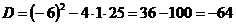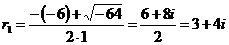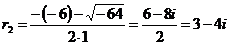Здесь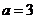 
, 
.
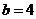Так как характеристическое уравнение имеет два комплексно-сопряженных корня, то общее решение дифференциального уравнения записывается в виде
.
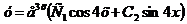Ответ: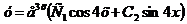
Пример 3. Найти частное решение уравнения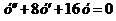 
, если 
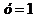и 
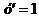при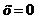 
.
Решение:
Составим характеристическое уравнение
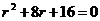
Найдем его корни
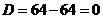
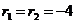
Так как корни действительные и равны, то общее решение данного дифференциального уравнения записывается в виде
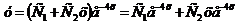
Продифференцируем общее решение
.
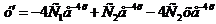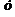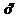Подставив начальные данные в выражения для и , получим систему уравнений
,
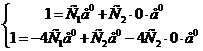
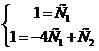откуда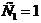 
и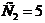 
.
Следовательно, искомое частное решение имеет вид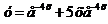 
.
Ответ: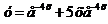
Пример 4. Найти частное решение уравнения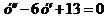 
, если 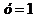и 
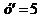при .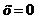
Решение:
Составим характеристическое уравнение
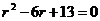
Найдем его корни
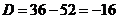
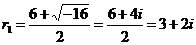
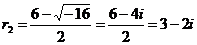
Так как корни комплексно-сопряженные, то общее решение данного дифференциального уравнения записывается в виде
.
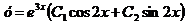Продифференцируем общее решение
.
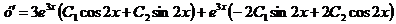
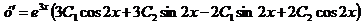
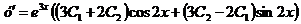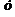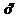Подставив начальные данные в выражения для и , получим систему уравнений
,
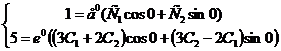
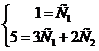откуда 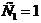и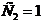 
.
Следовательно, искомое частное решение имеет вид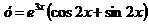 
.
Ответ: .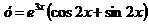
Задания для практической работы.
Вариант 1.
1. Решите уравнение: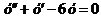 
.
2. Решите уравнение: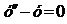 
.
3. Найти частное решение дифференциального уравнения 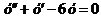, если 
.
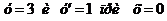4. Найти частное решение дифференциального уравнения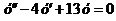 
, если 
.
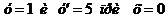Вариант 2.
1. Решите уравнение: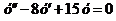 
2. Решите уравнение: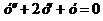 
3. Найти частные решения дифференциальных уравнений: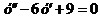 
, если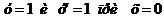 
4. Найти частные решения дифференциальных уравнений: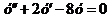 
, если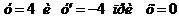 
Практическая работа № 6.