Дифференциальные уравнения второго порядка

Будем рассматривать уравнения второго порядка, разрешенные относительно второй производной:

y¢¢ = f(x, y, y¢). (11)

Теоремасуществования и единственности решения.Пусть функция
f(x, y, y¢) и ее частные производные ¶f/¶y, ¶f/¶y¢непрерывны в некоторой области D пространства переменных (x, y, y¢). Тогда для любой точки (x₀, y₀, y₀¢)этой области существует единственное решение уравнения (11), удовлетворяющее начальным условиям y(x₀) = y₀, y¢(x₀) = y₀¢.

Задачу отыскания решения (11) по заданным начальным условиям называют задачей Коши.

Далее будем рассматривать линейные дифференциальные уравнения второго порядка, которые имеют следующий общий вид:

y¢¢ + p(x)y¢ + q(x)y = f(x), (12)

где y – искомая функция, p(x), q(x), f(x)–заданные функции, непрерывные на некотором интервале (a, b). Если f(x) = 0, то (12) называется линейным однородным уравнением, если f(x) ¹ 0, –то неоднородным. Уравнение (12) при любых начальных условиях имеет единственное решение задачи Коши.

В дальнейшем рассматриваем (12) в случае, когда p(x), q(x) –постоянные величины, т.е. имеем уравнение

y¢¢ + p×y¢ + q×y = f(x), p, q = const. (13)

Теперь рассмотрим однородное уравнение

y¢¢ + p×y¢ + q×y = 0,(14)

соответствующее (13). Ищем решение (14) в виде y = e^kx, где k – некоторое число. Подставляя y = e^kx в (14), получаем k²×e^kx + k×p×e^kx + q×e^kx = 0 или

k² + k×p + q = 0. (15)

Если k – корень уравнения (15), то функция y = e^kx – решение однородного уравнения (14). Уравнение (15) называется характеристическим уравнением для дифференциального уравнения (14). Вид общего решения (14) существенно зависит от того, какие корни имеет характеристическое уравнение. Обозначим эти корни через k₁ и k₂. Справедливо следующее утверждение.

Теорема. Если корни характеристического уравнения (15) вещественные и k₁ ¹ k₂, то общее решение (14) имеет вид y = C₁×exp(k₁x) + C₂×exp(k₂x), где C₁, C₂ – произвольные постоянные. Если корни характеристического уравнения (15) вещественные и равны между собой (k₁ = k₂ = k), то общее решение (14) имеет вид y = (C₁ + C₂ x)e^kx. Наконец, если корни характеристического уравнения (15) комплексные, т.е. k₁ = a + i×b, k₂ = a – i×b, где i – мнимая единица, a, b – вещественные числа, то общее решение (14) будет иметь вид
y = e^ax[C₁×cos(bx) + C₂×sin(bx)].

Пример 1. Решить дифференциальное уравнение y¢¢ – 3y¢ + 2y = 0.

Решение. Здесь характеристическое уравнение имеет вид k² – 3k + 2 = 0, которое имеет два корня k₁ =1, k₂ =2. Итак, общее решение y = C₁e^x + C₂e^2x.

Пример 2. Решить дифференциальное уравнение 2y¢¢ + 8y¢ + 8y = 0.

Решение. Сокращая на 2, запишем исходное уравнение в виде

y¢¢ + 4y¢ + 4y = 0.

Соответствующее характеристическое уравнение k² + 4k + 4 = (k + 2)² = 0; его корни k₁ = k₂ = –2. Следовательно, общим решением будет y = (C₁ + C₂ x)×e^{– 2x} .

Пример 3. Решить дифференциальное уравнение y¢¢ + 4y¢ + 6y = 0.

Решение. Соответствующее характеристическое уравнение k² + 4k + 6 = 0имеет два комплексных сопряженных корня k₁ = –2 + i, k₂ = –2 – i. Общее решение исходного уравнения y = e^{– 2x} (C₁×cos(x ) + C₂×sin(x )).

Рассмотрим неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами вида (13). Общее решение получают несколькими способами. Рассмотрим метод вариации произвольных постоянных. Можно доказать, что общее решение линейного однородного уравнения (14) имеет вид

y_одн(x) = C₁×y₁(x) + C₂×y₂(x),

где C₁, C₂ – произвольные постоянные, а y₁(x), y₂(x) – линейно независимые функции (т.е. линейная комбинация a₁y₁(x) + a₂y₂(x) º 0 тогда и только, когда a₁ = a₂ = 0). Теперь переходим к решению неоднородного уравнения. Полагаем C₁, C₂ функциями от x, т.е. C₁ = C₁(x), C₂ = C₂(x). Варьируя произвольные постоянные, получаем общее решение уравнения (13) как

y = C₁(x)×y₁(x) + C₂(x)×y₂(x),

где C₁, C₂ определяется из системы

C₁¢×y₁(x) + C₂¢×y₂(x) = 0,

C₁¢×y₁¢(x) + C₂¢×y₂¢(x) = f(x);

при этом y₁(x), y₂(x) – частные линейно независимые решения соответствующего однородного линейного уравнения. Отметим, что

{ y₁ = exp(k₁x), y₂ = exp(k₂x) (k₁ ¹ k₂) }, { y₁(x) = e ^{k x}, y₂(x) = x×e ^{k x} },

{ y₁ = e^ax×cos(bx), y₂ = e^ax×sin(bx) } –

три пары линейно независимых функций, являющиеся частными решениями однородных линейных уравнений в соответствии с сформулированной теоремой.

Пример. Решить дифференциальное уравнение y¢¢ + 2y¢ + 2y = x×e ^–x.

Решение. Соответствующее однородное уравнение есть y¢¢ + 2y¢ + 2y = 0. Его характеристическое уравнение k²+2k+2=0имеет корни –1±i.Поэтому общее решение однородного уравнения имеет вид y_одн = e^–x (C₁×cos(x) + C₂×sin(x)).В качестве y₁(x), y₂(x) выбираем функции y₁(x) = e^–x cos(x), y₂(x) = e^–x sin(x). Варьируем C₁, C₂. Т.к.

y₁¢(x) = – e ^–x cos(x) – e ^–x sin(x), y₂¢(x) = – e ^–x sin(x) + e ^–x cos(x),

то

C₁¢×e^–x cos(x) + C₂¢×e^–x sin(x) = 0,

C₁¢×(– e^–x cos(x) – e^–x sin(x))+ C₂¢×(– e^–x sin(x) + e^–x cos(x)) = x×e^–x

или после сокращения на e^–x и преобразования

C₁¢×cos(x) + C₂¢×sin(x) = 0,

C₁¢×(cos(x) + sin(x))+ C₂¢×(sin(x) – cos(x)) = –x.

Используя правило Крамера для решения этой системы, находим C₁¢, C₂¢:

C₁¢=D₁/D, C₂¢=D₂/D,

где

D= =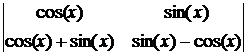

=cos(x)×(sin(x)–cos(x)) – sin(x)×(cos(x)+sin(x))= – cos²(x) – sin²(x) = –1.

D₁ = 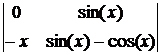= x×sin(x), D₂ = 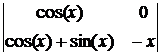= –x×cos(x).

Получаем C₁¢= –x×sin(x), C₂¢= x×cos(x). Теперь определяем C₁(x), C₂(x):

C₁(x) = ò (–x×sin(x))dx + C₁^*, C₂(x) = ò x×cos(x)dx + C₂^*,

где C₁^*, C₂^*–новые произвольные постоянные. Применяя метод интегрирования по частям, получаем

C₁(x) = x×cos(x) – sin(x) + C₁^*, C₂(x) = x×sin(x) + cos(x) + C₂^*.

Теперь выписываем общее решение исходного неоднородного линейного уравнения:

y = C₁(x)×y₁(x) + C₂(x)×y₂(x) =

= e ^–x [(x×cos(x) – sin(x) + C₁^*)×cos(x) + (x×sin(x) + cos(x) + C₂^*)×sin(x)].

Упрощая, получаем общее решение в более компактном виде:

y = e ^–x [C₁^*cos(x) + C₂^*sin(x) + x].

Пример. Решить задачу Коши для дифференциального уравнения

y¢¢+ y¢= x с начальными условиями y(0)=1, y¢(0) =1.

Решение. Соответствующее однородное уравнение есть y¢¢+ y¢= 0. Решая соответствующее ему характеристическое уравнение k² + k =0, получаем k₁=0, k₂= –1, откуда y_одн = C₁×e^0x + C₂×e ^{– x} = C₁×1 + C₂×e ^{– x}. Здесь в качестве y₁(x), y₂(x) выбираем функции y₁(x) = 1, y₂(x) = e ^–x . Варьируем C₁, C₂:

C₁¢×1 + C₂¢×e ^–x = 0, или C₁¢ + C₂¢×e ^–x = 0,

C₁¢×(1)¢+ C₂¢×(e ^–x)¢ = x –C₂¢×e ^–x = x.

откуда C₂¢= –x×e ^x, C₁¢= –C₂¢×e ^–x =x. Интегрируя по частям, находим C₁(x), C₂(x):

C₁(x) = ò x dx + C₁^* = + C₁^*, C₂(x) = – ò x×e^x dx + C₂^* = e^x (1–x) + C₂^*.

Теперь выпишем общее решение исходного уравнения y¢¢+ y¢= x:

y(x) = C₁(x)×y₁(x) + C₂(x)×y₂(x) = C₁(x)×1 + C₂(x)×e^{– x} =

= + C₁^* + (e^x (1–x) + C₂^*)×e^–x = – x + 1 + C₁^* + C₂^*×e^–x,

где C₁^*, C₂^*– произвольные постоянные. Теперь найдем частное решение, удовлетворяющее начальным условиям y(0)=1, y¢(0) =1. Имеем

y(0) = 1 + C₁^* + C₂^*= 1,

y¢(0) = ( – x + 1 + C₁^* + C₂^*×e^–x)¢_x=0 = (x – 1 – C₂^*×e^–x)_x=0 = –1 – C₂^*= 1.

Решая полученную систему, находим C₁^* и C₂^*: C₁^* = – C₂^* = 2. Итак, решая задачу Коши, однозначно определили значения постоянных C₁^*, C₂^*. Имеем

y = – x + 1 + C₁^* + C₂^*×e^–x = – x + 1 + 2 – 2e^–x.

Теперь можно записать окончательный ответ: y = – x – 2e^–x + 3.

9.3. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПРОИЗВОЛЬНОГО ПОРЯДКА
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

Рассмотрим линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами. Оно имеет вид

a₀y⁽ⁿ⁾ + a₁y^{(n – 1)} + … + a_{n – 1}y¢ + a_n y = 0. (16)

Для его решения следует составить характеристическое уравнение

a₀kⁿ + a₁k^{n – 1} + … + a_n–1k + a_n = 0 (17)

и найти все его корни. Общее решение содержит n произвольных постоянных и является линейной комбинацией частных решений следующих четырех типов.

1. Если k – вещественный и простой корень характеристического уравнения (17), то ему соответствует частное решение e^kx.

2. Если k – вещественный корень кратности m, то ему соответствует серия частных решений e^kx, xe^kx, … , x^m–1×e^kx.

3. Если k = a ± i×b – пара комплексно сопряженных корней характеристического уравнения (17) кратности 1, то этой паре соответствует пара частных решений: e^ax cos(bx) и e^ax ×sin(bx).

4. Если k = a ± i×b – пара комплексно сопряженных корней характеристического уравнения (17) кратности s, то этой паре соответствует серия частных решений:

e^ax ×cos(bx), x×e^ax ×cos(bx), …, x^s–1 e^ax ×cos(bx),

e^ax ×sin(bx), x e^ax ×sin(bx), …, x^s–1 e^ax ×sin(bx).

Пример 1. Решить дифференциальное уравнение y⁽⁵⁾ – 2y⁽⁴⁾ – 16y¢ + 32y =0.

Решение. Данному уравнению соответствует характеристическое уравнение k⁵ – 2k⁴ – 16k + 32 = 0. Для его решения перепишем это характеристическое уравнение в виде

k⁴ (k–2) – 16(k–2) = (k⁴ – 16)×(k–2) = (k² – 4)×(k² +4)×(k–2) = (k–2)²×(k+2)×(k² + 4).

Имеем следующие корни: k₁ = –2(кратность 1),k₂ = 2 (кратность 2), k_3,4 = ±2i (кратность 1). В силу вышесказанного получим общее решение

y = C₁e^–2x + (C₂ + C₃ x)e^2x + C₄ cos(2x) + C₅ sin(2x),

где C₁, …, C₅ – произвольные постоянные.

Пример 2. Решить дифференциальное уравнение y⁽⁶⁾ + 6y⁽⁴⁾ + 9y⁽²⁾ = 0.

Решение. Характеристическое уравнение имеет вид k⁶ + 6k⁴ + 9k² = 0. Запишем его в виде k² (k⁴ + 6k² + 9) = k² (k² + 3)² = 0. Получаем корни k₁ = 0 (кратность 2), k_2,3 = ±×i (кратность 2). Общее решение имеет вид

y = C₁ + C₂ x + (C₃ + C₄ x)×cos(x) + (C₅ + C₆ x)×sin(x),

где C₁, …, C₆ – произвольные постоянные.

Пример 3.Решить дифференциальное уравнение y⁽⁵⁾ + y⁽⁴⁾ + y⁽³⁾ = 0.

Решение. Характеристическое уравнение имеет вид k⁵ + k⁴ + k³ = 0. Запишем его в виде k³ (k² + k + 1) = 0.Получаем корни

k₁ = 0 (кратность 3), k_2,3 = (кратность 1). Общее решение имеет вид

y = C₁ + C₂ x + C₃ x² + C₄ ×e^{– x / 2} cos( x) + C₅×e^{– x / 2}×sin( x),

где C₁, …, C₅ – произвольные постоянные.

Задача Коши. Требуется найти решение уравнения (16), удовлетворяющее условиям y(x₀) = y₀, y¢(x₀) = y₀¢, … , y^(n–1)(x₀) = y₀^(n–1).

Доказывается, что задачи Коши для (16) имеет единственное решение.

Пример. Требуется найти решение уравнения y⁽⁴⁾ – y = 0, удовлетворяющее начальным условиям y(0) =1, y¢(0) =0, y¢¢(0) =2, y¢¢¢(0) =0.

Решение. Решая характеристическое уравнение k⁴ – 1 =0, получаем корни k_1,2 = ±1, k_3,4 = ±i(все кратности 1), после чего записываем общее решение

y(x) = C₁e^x + C₂ e^{– x} + C₃ cos(x) + C₄ sin(x),

где C₁, C₂, C₃, C₄ – произвольные постоянные. В дальнейшем определим значения C₁, C₂, C₃, C₄ , решив задачу Коши. Вычислим производные y(x) вплоть до 3-го порядка:

y¢(x) = C₁e^x – C₂ e^{– x} – C₃ sin(x) + C₄ cos(x),

y¢¢(x) = C₁e^x + C₂ e^{– x} – C₃ cos(x) – C₄ sin(x),

y¢¢¢(x) = C₁e^x – C₂ e^{– x} + C₃ sin(x) – C₄ cos(x).

С учетом начальных условий определяем постоянные C₁, C₂, C₃, C₄ :

y(0) = C₁ + C₂ + C₃ = 1, y¢(0) = C₁ – C₂ + C₄ = 0,

y¢¢(0) = C₁ + C₂ – C₃ =2, y¢¢¢(0) = C₁ – C₂ –C₄ = 0.

Имеем C₁+C₂ = , C₁ – C₂ = 0, откуда C₁ = C₂ = , C₃ = –, C₄ = 0.

Таким образом, y(x) = (e^x + e^{– x}) – cos(x).