Тема: Вычисление пределов. Раскрытие неопределенностей.
Цели работы: получить представление о пределах, их свойствах, замечательных пределах, теореме Лопиталя и научиться вычислять пределы, раскрывать различные виды неопределенностей.
Краткое изложение темы.
Число А называется пределом функции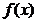 
при 
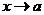, если для любого сколь угодно малого 
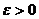найдется такое 
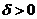, что 
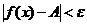при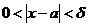 
. Это записывают так: 
.
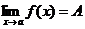Свойства пределов:
Если существуют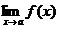 
и 
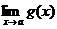, то
1) 
,
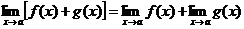2) 
,
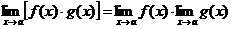3) 
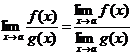(при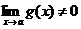 
).
Используются также следующие пределы:
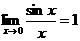(первый замечательный предел);
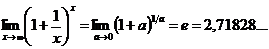(второй замечательный предел).
Правило Лопиталя раскрытия неопределенностей.
Пусть в некоторой окрестности точки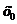 
(кроме, быть может, самой точки 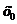) функци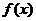и 
и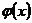 
дифференцируемы и 
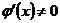. Ес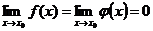ли 
или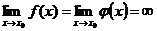 
, т. е. частное 
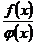в точке 
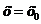представляет собой неопределенность вида 
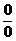или 
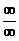, то
,
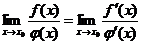если предел в правой части этого равенства существует.
Если частное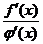 
в точке 
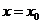также есть неопределенность вида 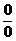или 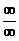и производные 
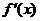и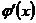 
удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т. д.
В случае неопределенности вида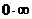 
или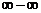 
следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида 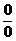или 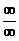и далее воспользоваться правилом Лопиталя.
Примеры выполнения заданий.
Пример 1. Найти предел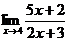 
.
Решение:
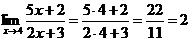
Ответ: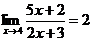 
Пример 2. Найти предел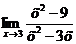 
.
Решение:
Имеем неопределенность вида .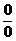
.
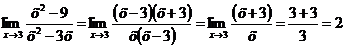Ответ: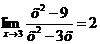 
Пример 3. Найти предел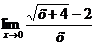 
.
Решение:
Имеем неопределенность вида .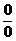
Умножим числитель и знаменатель дроби на сумму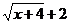 
.
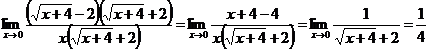
Ответ: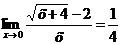 
.
Пример 4. Найти предел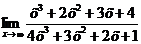 
.
Решение:
Это – неопределенность вида 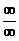. Разделим числитель и знаменатель дроби на старшую степень 
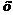, т.е. на 
:
.
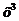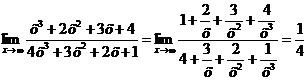Ответ: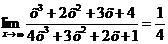 
.
Пример 5. Найти предел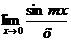 
.
Решение:
Используя первый замечательный предел, имеем
.
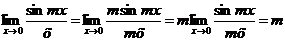Ответ: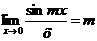 
.
Пример 6. Найти предел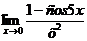 
.
Решение:
Имеем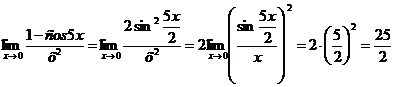 
.
Здесь мы воспользовались результатом предыдущего примера, приняв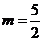 
.
Ответ: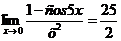 
.
Пример 7. Найти предел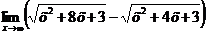 
.
Решение:
Здесь имеет место неопределенность вида 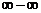. Умножим и разделим данное выражение на 
:
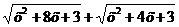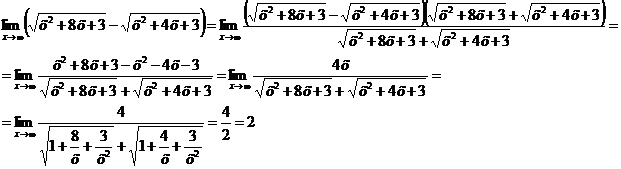
Ответ: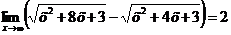 
Пример 8. Найти предел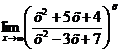 
.
Решение:
Делением числителя на знаменатель выделим целую часть:
.
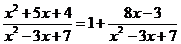Таким образом, при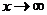 
данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределенность вида 
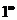). Преобразуя функцию так, чтобы использовать второй замечательный предел, получим
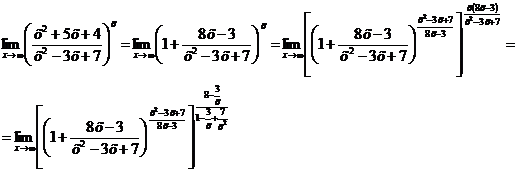
Так как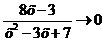 
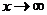при , то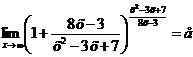 
.
Учитывая, что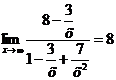 
, находим 
.
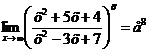Ответ: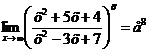
Пример 9. Найти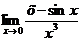 
.
Решение:
Это – неопределенность вида 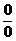. Имеем
,
так как 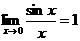. Здесь правило Лопиталя применено дважды.
Ответ: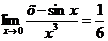 
.
Задания для практической работы.
Вариант № 1.
Вычислите пределы:
 . | ||
 . | ||
 | ||
 | ||
 | ||
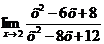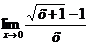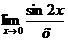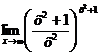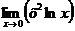| Дополнительные задания: | ||
 | ||
 | ||
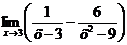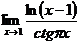Вариант № 2.
Вычислите пределы:
 | ||
 | ||
 | ||
 | ||
 | ||
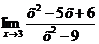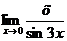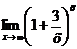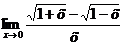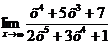| Дополнительные задания: | ||
 | ||
 | ||
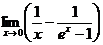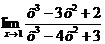Практическая работа № 3.
Тема: Дифференцирование функций.
Цели работы: закрепить умение находить производные по основным правилам дифференцирования, научиться дифференцировать сложные и неявные функции.
Краткое изложение темы.