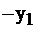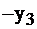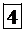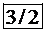Прикладные задачи математического программирования
Прикладные задачи математического программирования
Учебное пособие
Омск
Издательство ОмГТУ
Рассказова Марина Николаевна, доцент
Рыженко Любовь Степановна, старший преподаватель
Учебное пособие предназначено для студентов 2-го курса экономических специальностей дневного, вечернего и заочного обучения. В пособии рассмотрены основные темы прикладного раздела математики – линейного программирования, изучающиеся в общем курсе высшей математики; показана возможность решения прикладных задач на компьютере.
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
Редактор
ИД___________ от ___________
Подписано в печать . Бумага офсетная. Формат 60х84 1/16
Отпечатано на дупликаторе. Усл. печ. л. . Уч.-изд. л. .
Тираж 50 экз. Заказ .
__________________________________________________________
Издательство ОмГТУ. 644050, г. Омск, пр-т Мира, 11
Типография ОмГТУ
«В мире не происходит ничего, в чем бы не был бы виден смысл какого-нибудь максимума или минимума»
Леонард Эйлер
ГЛАВА I
ГЛАВА II
Основные типы задач линейного
программирования и методы их решения
Задача 4 (о рационе).
Необходимо составить рацион, включающий не менее 33 единиц вещества А, не менее 23 единиц питательного вещества В, не менее 12 единиц С. Для этого используются 3 вида продуктов. Данные о содержании питательных веществ в каждом виде продукта заданы таблицей 2.3. Также известны стоимости одной единицы каждого продукта. Нужно составить наиболее дешевый рацион.
Таблица 2.3
| продукты | Вещества | Стоимость 1 ед. продукта | ||
| А | В | С | ||
| I | ||||
| II | ||||
| III |
Для понимания задачи можете представить себе, что вещества А, В, С – это жиры, белки, углеводы, а продукты I, II, III. Тогда первая строка таблицы показывает содержание в 1 ед. продукта I: 4 ед. белка, 3 ед. жиров, 1 ед. углеводов; вторая строка содержание белков, жиров, углеводов в 1 ед. продукта II и т. д.
Если постановка задачи ясна, приступим к построению математической модели. Опять стоит вопрос: что обозначить за неизвестные. В качестве ответа к поставленной задаче мы должны предложить рацион, т. е. указать, сколько и каких продуктов взять, чтобы необходимое количество питательных веществ было соблюдено, и при этом чтобы его стоимость была минимальной.
Обозначим за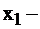 
количество продуктов вида I в рационе, за 
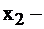количество продуктов вида II, и соответственно 
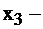количество III-го вида продукта в рационе. Тогда, вещества А при потреблении продуктов типа I получается 
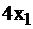, при потреблении II вида продукта – 
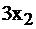, при потреблении III – 
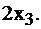Всего вещества А необходимо употребить по условию задачи не менее 33 единиц, следовательно: 
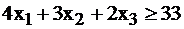. Аналогично рассуждая с веществом В, имеем: 
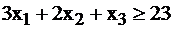и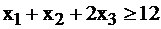 
для С.
Таким образом, получим систему ограничений:
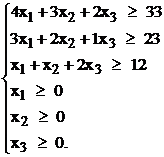(7)
Переменные неотрицательны по смыслу задачи. При этом стоимость рациона выражается функцией
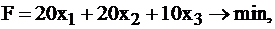т. к. 20, 20, 10 – стоимость одной единицы продуктов I, II, III типов соответственно, а в рационе их содержится 
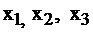единиц.
Система ограничений (7) и целевая функция составляют математическую модель исходной задачи. Решить ее, значит, найти такие 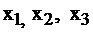, удовлетворяющие системе ограничений и обращающие значение функции F в минимальное.
Задача 5 (о раскрое).
Пусть из заготовок для замков-молний длиной 1 метр выпускаются замочки размером 12 см, 18 см и 35 см. Известны различные варианты раскроя метровых заготовок на замочки и остатки для каждого варианта. Также заданы минимальные потребности в замочках каждой длины. Необходимо определить: сколько заготовок нужно раскроить по каждому возможному варианту раскроя, чтобы получить необходимое количество замочков, при этом количество отходов должно быть минимальным.
Рассмотрим несколько возможных вариантов раскроя (в таблице 2.4 указано три), заметьте, что перечислены не все.
Таблица 2.4
| Типы замков-молний | Варианты раскроя | Потребности в замках | ||
| 12 см | ||||
| 18 см | ||||
| 35 см | ||||
| отходы |
Построение модели.
Обозначим за 
– количество метровых заготовок, раскраиваемых по 1-му варианту, за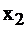 
– количество метровых заготовок, раскраиваемых по 2-му варианту, за 
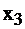– количество метровых заготовок, раскраиваемых по 3-му варианту.
Тогда посчитаем количество замков:
длиной 12 см: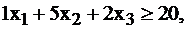 
длиной 18 см: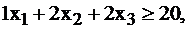 
(8)
длиной 35 см: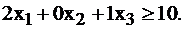 
Общее количество отходов определяет целевую функцию:
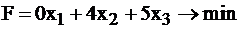
Система ограничений (8) вместе с целевой функцией составляют математическую модель задачи о раскрое.
Случай 1.
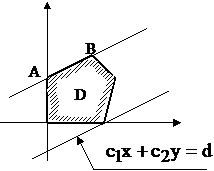При перемещении прямой 
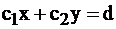«вход» или «выход» произойдет по стороне многоугольника (как на рисунке). Это случится, если в многоугольнике есть стороны, параллельные прямой .
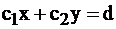В этом случае точек «выхода» («входа») бесконечное множество, а именно любая точка отрезка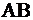 
.
Это означает, что целевая функция принимает максимальное (минимальное) значение не в одной точке, а во всех точках, лежащих на соответствующей стороне многоугольника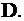 
Случай 2.
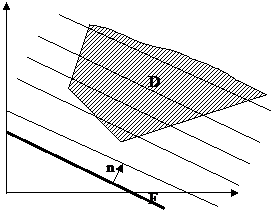Рассмотрим случай, когда область допустимых значений открыта, как в примере 3 § 2.3.
В случае открытой области целевая функция может быть задана таким образом, что соответствующая ей прямая не имеет точки «выхода» (или «входа») из области.
Тогда максимальное (минимальное) значение функции не достигается ни в какой точке, говорят, что функция неограниченно возрастает (убывает).
Рассмотрим графический способ решения на примере задачи 3 (о составлении плана) §2.1, смотри ниже рис.2.5.
Необходимо найти максимальное значение целевой функции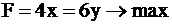 
при системе ограничений:
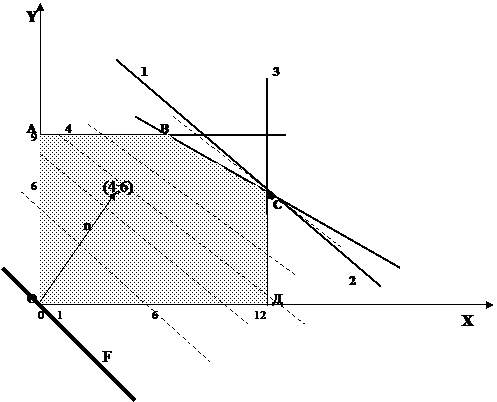
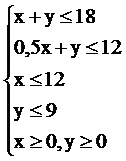
Рис. 2.5 Графическое решение задачи ЛП
1. Построим область допустимых значений, являющуюся решением системы неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами.
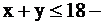полуплоскость ниже прямой 
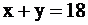(обозначена цифрой 1);
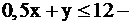полуплоскость ниже прямой 
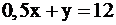(2);
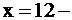прямая, параллельная оси OY (3); 
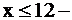полуплоскость левее (3);
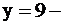параллельна оси OX (4), 
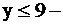полуплоскость ниже 
;
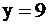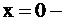ось OY; 
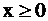– полуплоскость правее оси OY;
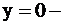ось OX; 
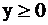– полуплоскость выше оси OX.
2. Пересечением всех этих полуплоскостей является, очевидно, пятиугольник ОАВСД с вершинами в точках О(0;0), А(0;9), В(6;9), С(12;6), Д(12;0). Этот пятиугольник и образует область допустимых значений задачи.
3. Рассмотрим целевую функцию задачи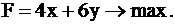 
Вектор градиента целевой функции имеет вид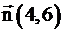 
. Построим прямую, перпендикулярную этому вектору: 
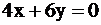. Будем двигать эту прямую параллельным образом. Из всего семейства прямых 
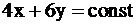последней вершиной, через которую пройдет прямая, при выходе за границу многоугольника, будет вершина 
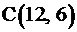. Именно в ней 
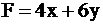достигнет своего максимального значения.
Значит, при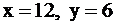 
функция F достигает своего максимального значения и равна 
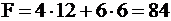. Точка (12; 6) удовлетворяет всем неравенствам системы ограничений, и в ней значение целевой функции оптимально: 
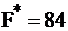(оптимальное значение будем обозначать «*»). Задача решена.
Ответ: необходимо выпустить 12 изделий I вида и 6 изделий II вида, при этом прибыль составит 84 ед.
Еще раз обратим внимание на то, что графический метод применялся нами для решения задач, которые имели в системе ограничений только две переменных. В принципе этот метод может применяться и для систем неравенств, имеющих три переменных. Геометрически ситуация будет иная, более сложная для изображения, роль прямых будут играть плоскости в трехмерном пространстве, а решением неравенства от трех переменных будет являться полупространство, находящееся по одну сторону от плоскости. Роль областей будут играть многогранники, являющиеся пересечением полупространств. Идея метода остается той же.
Каноническая форма задач ЛП
Одним из универсальных методов линейного программирования является симплексный метод, который применим для задач, имеющих каноническую форму.
Определение. Задача ЛП имеет каноническую форму, если:
1) все ограничения системы состоят только из уравнений,
2) переменные неотрицательны,
3) целевую функцию необходимо максимизировать.
Однако в большинстве экономических задач чаще всего в систему ограничений первоначально входят не только уравнения, но и неравенства, как было у нас в задачах 2, 3, 4, 5.
Любая общая задача ЛП может быть приведена к канонической форме. Выполнение первого условия достигается путем введения новых (или их называют дополнительными) переменных. Вернемся к задаче 3. Система ограничений (3) этой задачи состоит из четырех неравенств. Введя дополнительные переменные: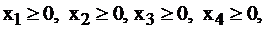 
можно перейти к системе ограничений:
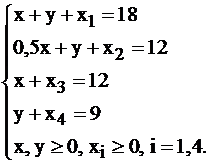(9)
Эти дополнительные переменные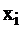 
имеют конкретный экономический смысл, а именно означают величину неиспользованного времени работы (простоя) машины 
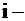го вида. Например, если бы машины первого вида работали все 18 ч., то 
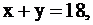следовательно, 
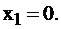Но мы допускаем возможность неполного использования времени работы 1-й машины 
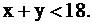В этом случае 
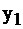приобретает положительное значение и может рассматриваться как неиспользованный лимит времени. Например, зная решение этой задачи из результатов § 2.3, 
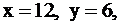мы можем из системы ограничений (9) сделать вывод, что 
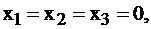а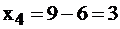 
. То есть машины 1-го , 2-го, 3-го вида используют свое рабочее время полностью, а вот 4-я машина загружена лишь наполовину: 3 часа при заданном оптимальном плане простаивает. Возможно, после таких выводов руководителю предприятия захочется загрузить ее другой работой, сдать в аренду на это время и т. д.
Итак, введением дополнительных переменных мы можем любое ограничение типа неравенства привести к уравнению.
Рассмотрим задачу о смеси (4 из §2.1). Система ограничений имела вид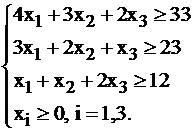 
Неравенства были обращены в сторону «больше», поэтому, вводя дополнительные переменные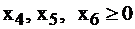 
их необходимо отнять от левой части, чтобы уравнять ее с правой. Получим систему ограничений в канонической форме:
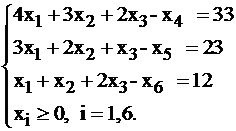
Переменные 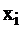также будут иметь экономический смысл. Если вы вспомните практическое содержание задачи, то переменная 
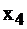будет означать количество излишнего вещества А в смеси, 
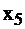– количество излишков вещества В в смеси, 
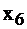– количество излишков С в смеси.
Выполнение второго условия: задача нахождения минимального значения целевой функции может быть сведена к нахождению максимума для функции –F, ввиду очевидности утверждения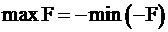 
.
|
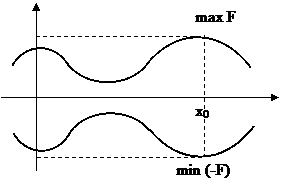Посмотрите на рис. 2.6, если в какой-то точке 
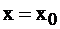функция 
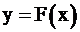достигает своего максимума, то функция 
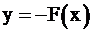, симметричная ей относительно оси OX, в этой же точке 
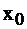достигнет минимума, причем 
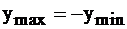при 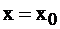. Вып
Выполнение третьего условия – неотрицательности переменных достигается представлением отрицательной переменной в виде разности двух переменных, которые уже в свою очередь неотрицательны: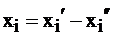 
.
Идея симплексного метода
Симплексный метод является универсальным методом линейного программирования. Его алгоритм состоит из ряда шагов, следуя которым, вы приходите к решению задачи ЛП. Сейчас нас будет интересовать аналитическая идея этого метода, которая при общем взгляде на алгоритм или на «замурованную» программу в ЭВМ не столь ясна, как если бы рассмотреть ее на конкретном примере.
Итак, если мы решаем ЗЛП в канонической форме, то система ограничений – это обычная система линейных уравнений. При решении задач ЛП получаются системы линейных уравнений неопределенные, т.е имеющие множество решений.
Например, пусть есть система
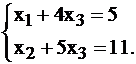
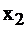Здесь число уравнений равно 2, а неизвестных 3, уравнений меньше – система недоопределена. Выразим и через :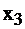
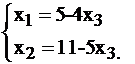
Это общее решение системы. Если переменной 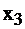придавать любые, произвольные числовые значения, то будем находить частные решения системы. Например, 
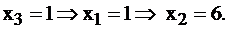Имеем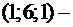 
частное решение. Пусть 
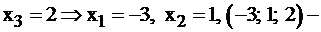другое частное решение. Таких частных решений бесконечно много.
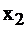Совокупность переменных и образует базис: 
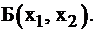Переменные и 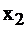называются базисными, а переменная 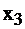– свободной. Если 
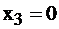, то полученное частное решение (5,11,0) называется базиснымрешением, соответствующим базису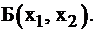
Теоремы двойственности
Двойственность является фундаментальным понятием в теории линейного программирования. Основные результаты теории двойственности заключены в двух теоремах, называемых теоремами двойственности.
Теорема 1 (первая теорема двойственности).
Если одна из пары двойственных задач I и II разрешима, то разрешима и другая, причем значения целевых функций на оптимальных планах совпадают,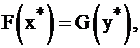 
где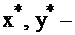 
оптимальные решения задачи I и II.
Теорема 2(вторая теорема двойственности).
Планы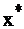 
и 
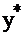оптимальны в задачах I и II тогда и только тогда, когда при подстановке их в систему ограничений задачи I и II соответственн, хотя бы одно из любой пары сопряженных неравенств обращается в равенство.
Доказательства теорем опускаем, а на конкретном примере нашей задачи покажем, как они работают. Теорема 2 позволяет по решению одной задачи находить решение двойственной.
Итак, имеем оптимальное решение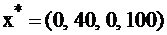 
и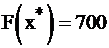 
задачи I. Найдем решение двойственной задачи II 
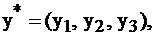не прибегая к симплекс-методу, а воспользовавшись второй теоремой двойственности и известным оптимальным планом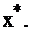 
Для этого необходимо подставить оптимальное решение 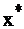в каждое неравенство системы ограничений и посмотреть, как оно выполняется: строго или нет.
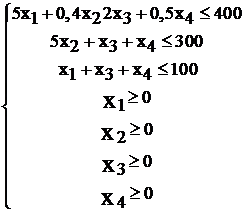
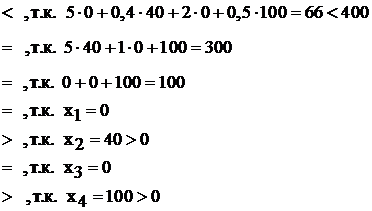
Поскольку 1, 5, 7 неравенства строгие (имеют знак «<» или «>»), то соответствующие им неравенства в задаче II из пары сопряженных по II теореме двойственности обязаны обратиться в равенства, имеем:
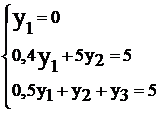Решаем систему, находим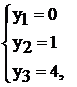 
т.е.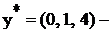 
оптимальное решение. Заметим, что действительно I-я теорема двойственности справедлива: 
.
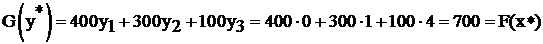Итак, в силу второй теоремы двойственности, мы быстро нашли оптимальное решение задачи II, пользуясь условием обращения в равенство хотя бы одного из пары сопряженных неравенств в системах ограничений двойственных задач.
Между переменными исходной задачи и переменными двойственной существует связь. А именно, после приведения обеих задач I и II к каноническому виду основные и дополнительные переменные задач соответствуют друг другу следующим образом:
основные дополнительные
 |  | ||
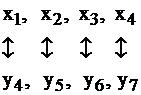
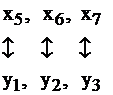
дополнительные основные
Установив такую связь, внимательный читатель заметит, что, решив задачу I симплекс-методом, и получив последнюю симплекс–таблицу (табл. 2.15), мы фактически решим и задачу II. Запишем таблицу 2.16, учитывая соответствие между переменным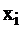и и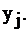 
Таблица 2.16
 |  |  |  | |||
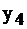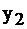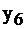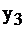| свободные базис | 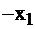 | 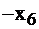 | 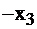 | 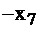 | правые части | |
| | | |||||
 | | |||||
 | | |||||
 |
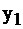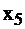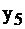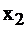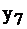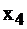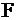Если последняя симплекс-таблица известна, то, пользуясь соответствием, можно найти решение двойственной задачи. Переменные, которые в левом столбце: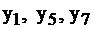 
обязаны равняться 0, т.к. 
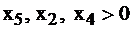строго. А переменные из верхней строки 
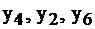принимают значения нижней строки 1, 1, 0, 4 соответственно, т.к. им соответствующие переменные 
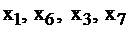равны 0 как свободные. Итак, из последней таблицы задачи II, не проводя никаких вычислений, и пользуясь лишь соответствием переменных, можно определить 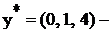оптимальное решение. 
Необходимо знать оба способа решения двойственной задачи. Т.к. если исходная задача решалась на компьютере, например, в приложении Excel , и вы не имеете симплекс-таблиц, но знаете оптимальный план, по второй теореме двойственности найдете решение. Если же вы находили исходный план вручную, нет необходимости решать систему линейных уравнений, достаточно посмотреть в последнюю симплекс-таблицу. Итак, мы научились по решению исходной задачи находить решения двойственной. Это возможно благодаря глубокой связи между переменным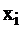и и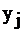 
. Осталось разобраться, каково экономическое содержание этих взаимосвязей.
И теории двойственности
Исходная задача I имела следующий экономический смысл: основные переменные 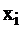обозначали количество произведенной продукции i-го вида, дополнительные переменные обозначали излишек соответствующего вида ресурсов, каждое из неравенств выражало собой расход определенного вида сырья в сравнении с запасом этого сырья. Целевая функция определяла прибыль при реализации всей продукции. Предположим теперь, что предприятие имеет возможность реализовывать сырье на сторону. Поставим вопрос: какую минимальную цену надо установить за единицу каждого вида сырья при условии, что доход от реализации всех его запасов должен быть не меньше дохода от реализации продукции, которая может быть выпущена из этого сырья. Иначе говоря, выгодно было бы продавать сырье, чем производить изделия. Переменные двойственной задачи 
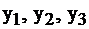имеют смысл – это условные относительные (теневые) цены за ресурсы 1, 2, 3 вида соответственно. Тогда доход от продажи видов сырья, расходуемого на производство одной единицы продукции I, равен: 
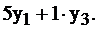Но, если мы хотим, чтобы доход от продажи сырья был не меньше, чем от реализации продукции, то должно быть 
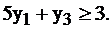Именно в силу такого экономического толкования система ограничений двойственной задачи принимает вид
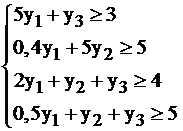
А целевая функция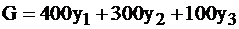 
подсчитывает условную суммарную стоимость всего имеющегося сырья. Понятно, что в силу I теоремы двойственности 
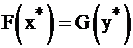равенство означает, что максимальная прибыль от продажи всей готовой продукции совпадает с минимальной условной ценой ресурсов. Итак, условные оптимальные цены 
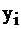показывают наименьшую стоимость ресурсов, при которой выгодно обращать эти ресурсы в продукцию, т.е. производить. Величина 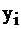показывает насколько увеличится значение целевой функции, если запас сырья увеличить на 1 ед.
Еще раз обратим внимание на то, что 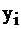– это лишь условные, предполагаемые, а не реальные цены на сырье. Иначе, читателю может показаться странным, что например, 
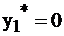. Этот факт вовсе не означает, что реальная цена 1–го ресурса нулевая, ничего бесплатного в этом мире нет. Равенство нулю условной цены означает лишь, что этот ресурс не израсходован полностью, имеется в излишке, недефицитен. Действительно, посмотрим на 1-е неравенство в системе ограничений задачи I, в котором подсчитывается расход 1-го ресурса: 
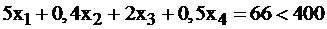. Его избыток составляет 
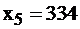ед. при данном оптимальном плане производства, и поэтому для производителя он недефицитен, его условная цена равна 0, его не надо закупать. Наоборот, ресурсы 2-й и 3-й используются полностью, причем 
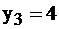а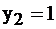 
, т.е. сырье третьего вида более дефицитно, чем второго, его условная цена больше. Если производитель продукции имел бы возможность приобретать дополнительно сырье к уже имеющемуся, с целью получения максимального дохода от производства, то, увеличив сырье 2-го вида на 1 единицу, он бы получил дополнительно доход в 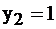денежных единиц, а увеличив на 1 ед. сырье 3-го вида, значение целевой функции увеличилось бы на 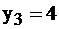ед.
Если перед производителем стоит вопрос: «выгодно ли производить какую-либо новую продукцию, при условии, что затраты на 1 единицу продукции составят 3, 1, 4 единицы сырья соответственно, а прибыль от реализации равна 23 единицам?», то в силу экономического истолкования задачи ответить на этот вопрос несложно. Поскольку затраты и условные цены ресурсов известны: затраты равны 3, 1, 4, а цены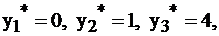 
значит можно посчитать суммарную условную стоимость ресурсов, необходимых для производства этой новой продукции: 
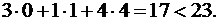Т.е. продукцию производить выгодно, т.к. прибыль от реализации превышает затраты на ресурсы, в противном случае, ответ бы на этот вопрос был отрицательным.
Замечание. Иногда при решении задач ЛП применяют двойственный симплекс-метод. Этот метод удобно применять при решении задачи о рационе, задачи о раскрое и некоторых других. Поскольку, решая исходную задачу, мы автоматически получаем решение двойственной, то иногда удобно выбирать, какую из задач решать. Двойственный симплекс–метод основан на очень простой идее. К данной задаче нужно построить двойственную, решить двойственную, а затем по её решению найти решение исходной.
Можно продемонстрировать на примере уже рассмотренной нами задачи о рационе.
I. 
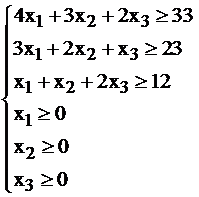II.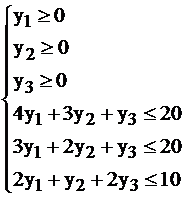 
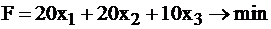
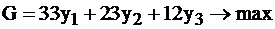
Решаем симплекс–методом задачу II (смотри табл.2.17-19).
Таблицы 2.17 Таблица 2.18
|
|
Таблица 2.19
| Баз. | 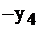 | 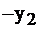 | 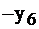 | Своб. |
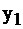| | -1/6 | |||
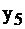| | -1/6 | |||
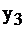| | -1/3 | 1/3 | 2/3 | |
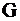 | 1/2 | 5/2 |
Выписываем решение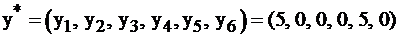 
. Найдем решение исходной, пользуясь II теоремой двойственности.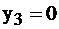 
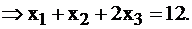
Так как неравенств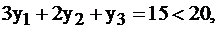о 
то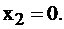 
Найдем и 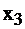из системы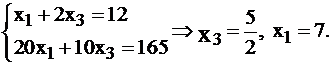 
Итак,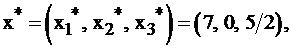 
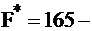решение исходной задачи о рационе.
Еще раз отметим, что мы воспользовались тем, что двойственная задача имела специальный вид, и ее удобно было решать, а затем уже вернуться к исходной. Но в силу тесной связи между этими двумя парами задач, на самом деле симплекс–таблицы, полученные сейчас, и ранее см.§ 2.7, совпадают с точностью до транспонирования. Фактически мы лишь упростили внешний вид табл. 2.10-2.12, избавив себя от излишних «минусов».
ГЛАВА III
Алгоритм метода потенциалов
Алгоритм состоит из трех основных шагов:
1) построение первоначального опорного плана.
2) проверка плана на оптимальность.
3) улучшение плана.
Шаг 1. Построение первоначального опорного плана.
Существует два наиболее часто применяемых метода для нахождения первого плана: метод наименьшей стоимости и метод северо-западного угла. Метод наименьшей стоимости позволяет найти план, наиболее близкий к оптимальному, метод северо-западного угла легче программируется, и поэтому до сих пор «живет». Но, если вы решаете задачу «вручную», то применение метода наименьшей стоимости, как правило, уменьшает количество итераций.
Идея метода наименьшей стоимости проста и отражается в названии метода. Сначала следует организовать перевозки к тем поставщикам, где стоимость минимальна. Рассмотрим конкретный пример.
Транспортная задача. Пусть имеется 4 поставщика некоторой продукции и 5 потребителей. Стоимости перевозок от i-го поставщика к j-му потребителю, а также потребности потребителей и возможности поставщиков заданы табл. 3.1
Таблица 3.1
| В1 | В2 | В3 | В4 | В5 | запасы | |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| А4 | ||||||
| потребности |
Эта транспортная задача является закрытой или сбалансированной, т.к. 24+12+18+16=60 и 11+13+26+10+10=60 – потребности равны запасам. Будем заполнять первую распределительную таблицу. Стоимости перевозок в новой таблице будем располагать в правом верхнем углу клеток, а в центр клеток помещать числа, соответствующие первоначальному опорному плану перевозок.
Итак, минимальная стоимость перевозки – это число 1, оно встречается на двух местах, с номерами (2, 4) и (3, 2). Выберем любое, к примеру, (2, 4). Рассуждаем: у поставщика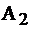 
имеется запас товара 12 ед., а потребителю 
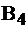требуется 10 ед., можем удовлетворить его потребности и привезти ему 10. Тогда у 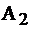останется в запасах 12-10=2 ед. Поместим в клетку (2, 4) наименьшее из чисел 10 и 12, т.е. перевозку 10. При этом заметим, потребности потребителя 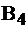удовлетворены, можем вычеркнуть 4-й столбец из рассмотрения, запомнив сбоку, что запасов осталось на втором складе 2 ед. (см.табл. 3.2).
Таблица 3.2
| В1 | В2 | В3 | В4 | В5 | запасы | |
| А1 | 21 | 19 | 11 | -12 | 12 | |
| А2 | 26 | 29 | 14 | 10 1 | 26 | 12/2 |
| А3 | 39 | 1 | 22 | - 8 | 25 | |
| А4 | 53 | 23 | 40 | -26 | 28 | |
| потребности | 10/0 |
В табл. 3.2 теперь снова ищем минимальный по стоимости элемент, это опять 1 на месте (3, 2). Записываем в эту клетку число 13, как наименьшее из чисел 13 и 18 и вычеркиваем 2-й столбец, потребности В2 удовлетворены (табл. 3.3).
Таблица 3.3
| В1 | В2 | В3 | В4 | В5 | запасы | |
| А1 | 21 | 19 | 11 | - 12 | 12 | |
| А2 | 26 | 29 | 14 | 10 1 | 26 | 12/2 |
| А3 | 39 | 131 | 22 | - 8 | 25 | 18/5 |
| А4 | 53 | 23 | 40 | – 26 | 28 | |
потребно< Наши рекомендации |