Плотность распределения и функция распределения показательной случайной величины, ее числовые характеристики.
Показательным (экспоненциальным)называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
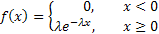
где - положительное число
Найдем закон распределения
F(x) = 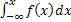 =
= 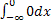 + λ
+ λ 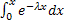 = 1- e-λx
= 1- e-λx
F(x) = 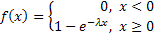
Интервал времени между двумя последовательными появлениями некоторого редкого события описывается случайной величиной, распределенной по показательному закону. Например, по показательному закону распределено время безотказной работы какого-либо устройства.
Найдем математическое ожидание и дисперсию.
∞
MX = 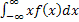 =
= 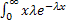 dx =
dx = 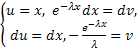 = λ(-
= λ(- 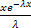 | +
| + 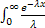 dx =
dx =
0
∞
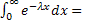 -
- 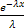 | =
| = 
Результат получен с использованием того факта, что
∞
xe-λx | = 0
Для нахождения дисперсии найдем величину MX2
MX2 = 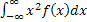 =
= 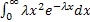
Дважды интегрируя по частям получаем
MX2 = 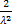
Тогда DX = MX2 – (MX)2 = 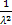
σX = 
Видно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.
Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.
P(a<X<b) = F(a) – F(b) = e-λa – e-λb
Показательное распределение широко используется в теории надежности.
45. Плотность распределения и функция распределения нормальной случайной величины (распределение Гаусса), ее числовые характеристики.
Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
f(x) = 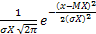
Нормальный закон распределения также называется законом Гаусса.
Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Можно легко показать, что параметры MX и σX , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.
Найдем функцию распределения F(x).
F(x) = 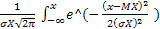
График плотности нормального распределения называется нормальной кривойили кривой Гаусса.
Нормальная кривая обладает следующими свойствами:
1) Функция определена на всей числовой оси.
2) При всех х функция распределения принимает только положительные значения.
3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю.
4) Функция является симметричной относительно прямой х = а, т.к. разность
(х – а) входит в функцию плотности распределения в квадрате.
Найдем математическое ожидание и дисперсию.
MX = 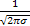
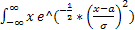 =
= 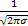
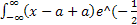 *(
*( 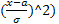 )dx =
)dx =
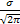
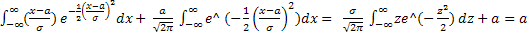
z = (x-a)/σ
Поскольку 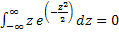 как интеграл по всей прямой от нечетной функции.
как интеграл по всей прямой от нечетной функции.
Таким образом, параметр а – математическое ожидание.
Найдем дисперсию нормальной случайной величины, снова применяя замену z = (x-a)/σ и интегрируя по частям:
DX = M(X-MX)2 = 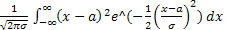 =
= 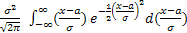 =
=
∞
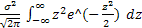 =
= 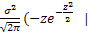 +
+ 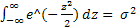
-∞
σ2 - это дисперсия, а σ – среднее квадратичное отклонение.
Случайная величина называется центрированной, если ее математическое ожидание равно 0. Для того, чтобы центрировать случайную величину, надо вычесть из нее математическое ожидание:
M(X – MX) = MX – MX = 0
Случайная величина называется нормированной, если ее дисперсия равна единице. Для того чтобы нормировать случайную величину, надо ее поделить на среднее квадратичное отклонение:
D( 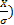 =
= 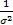 DX =
DX = 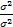 = 1
= 1
Центрированная и нормированная случайная величина называется стандартной.
