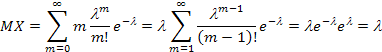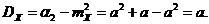Случайная величина принимает целые значения в промежутке от 0 до n с равной вероятностью. Вывести выражение для математического ожидания этой случайной величины.

Делала сама проверяйте ...

Х			...	n
Р	p	p	...	p

∞ ∞

MX = Σ x_i p_i =p Σ x_i т.к р конст, можно вынести за знак суммы

^{i=1 i=1}

а т.к сумма случайных величин от 1 (р*0=0) до n можно представить как арифметическую прогрессию, то

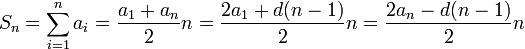
a₁=1 ,a_n=n , то получим: (1+n)n/2

получим:

1+n

MX = - np

Случайная величина принимает целые значения в промежутке от 0 до n с равной вероятностью. Вывести выражение для дисперсии этой случайной величины.

DX= M(x²)-(M(x)) ²

MX=∑ⁿ_i=1 x₁ p₁ = p ∑ⁿ_i=1 x₁

M(x)² = p (x²₁ +…x²_n)=p∑ⁿ_i=1 x²_i

D(x)= p∑ⁿ_i=1 x²_i – (p∑ⁿ_i=1 x_i)²

Вывести выражение для математического ожидания альтернативно распределенной случайной величины.

Альтернативной СВ, называется СВ Х, задаваемая рядом распределения

Х
р	1-р	р

МХ=0*(1-р)+1*р=р

М(Х²)=0²(1-р)+1²р=р

DX= М(Х²)-(МХ)²=р-р²=р(1-р)

Вывести выражение для дисперсии альтернативно распределенной случайной величины.

Альтернативной СВ, называется СВ Х, задаваемая рядом распределения

Х
р	1-р	р

МХ=0*(1-р)+1*р=р

М(Х²)=0²(1-р)+1²р=р

DX= М(Х²)-(МХ)²=р-р²=р(1-р)

Вывести выражение для математического ожидания случайной величины, распределенной по закону Пуассона.

Говорят, что СВ Х распределена по закону Пуассона с параметром λ, если она принимает значения 0,1,2,… с вероятностями

Λ^k

P_n(k)= - *e^-λ где λ≥0

K!

∞ λ^k ∞ λ^k ∞ λ^k-1

MX= Σ *k*- * e^-λ= Σ*k *- * e^-λ = e^-λλ Σ* -

^k=1 k! ^k=1 k(k-1)! ^k=1 (k-1)!

Предположим, что k-1=m, получим

∞ λ^m

MX =λ* e^-λ Σ -

^m=0 m!

∞ λ^m

Принимая во внимание, что Σ - имеем МХ= λ*e^-λ* e^λ =λ

^m=0 m!

DX= М(Х²)-(МХ)²= М(Х²)- λ²

∞ λ^k e^-λ ∞ k λ^k e^-λ ∞ λ^k-1 e^-λ

M(X²) = Σ k² - = Σ k - = λ Σ k -

^k=1 k! ^k=1 k(k-1) ^k=1 (k-1)!

∞ λ^k-1 e^-λ ∞ λ^k-1 e^-λ ∞ λ^k-1 e^-λ

= λ Σ[(k-1)+1] - = λ [Σ(k-1) - + Σ - ] .

^k=1 (k-1)! ^k=1 (k-1)! ^k=1 (k-1)!

Допустим k-1 =m, получим

∞ λ^m e^-λ ∞ λ^m e^-λ

M(X²) = λ[Σ m - + Σ - ]

^m=0 m! ^m=0 m!

Принимая во внимание, что

∞ λ^m e^-λ ∞ λ^m e^-λ ∞ λ^m

Σ m - = λ , Σ - = e^-λ Σ - = e^-λ e^λ

^m=0 m! ^m=0 m! ^m=0 m!

Имеем,

M(X²) = λ(λ-1)= λ²+λ

DX= λ²+λ- λ²= λ

Вывести выражение для дисперсии случайной величины, распределенной по закону Пуассона.

Говорят, что СВ Х распределена по закону Пуассона с параметром λ, если она принимает значения 0,1,2,… с вероятностями

Λ^k

P_n(k)= - *e^-λ где λ≥0

K!

∞ λ^k ∞ λ^k ∞ λ^k-1

MX= Σ *k*- * e^-λ= Σ*k *- * e^-λ = e^-λλ Σ* -

^k=1 k! ^k=1 k(k-1)! ^k=1 (k-1)!

Предположим, что k-1=m, получим

∞ λ^m

MX =λ* e^-λ Σ -

^m=0 m!

∞ λ^m

Принимая во внимание, что Σ - имеем МХ= λ*e^-λ* e^λ =λ

^m=0 m!

DX= М(Х²)-(МХ)²= М(Х²)- λ²

∞ λ^k e^-λ ∞ k λ^k e^-λ ∞ λ^k-1 e^-λ

M(X²) = Σ k² - = Σ k - = λ Σ k -

^k=1 k! ^k=1 k(k-1) ^k=1 (k-1)!

∞ λ^k-1 e^-λ ∞ λ^k-1 e^-λ ∞ λ^k-1 e^-λ

= λ Σ[(k-1)+1] - = λ [Σ(k-1) - + Σ - ] .

^k=1 (k-1)! ^k=1 (k-1)! ^k=1 (k-1)!

Допустим k-1 =m, получим

∞ λ^m e^-λ ∞ λ^m e^-λ

M(X²) = λ[Σ m - + Σ - ]

^m=0 m! ^m=0 m!

Принимая во внимание, что

∞ λ^m e^-λ ∞ λ^m e^-λ ∞ λ^m

Σ m - = λ , Σ - = e^-λ Σ - = e^-λ e^λ

^m=0 m! ^m=0 m! ^m=0 m!

Имеем,

M(X²) = λ(λ-1)= λ²+λ

DX= λ²+λ- λ²= λ

Вывести выражение для математического ожидания случайной величины, распределенной по геометрическому закону.

СВ Х называется распределенной по геометрическому закону с параметром р ( где р? [0;1]), если она принимает значения 1, 2,3 ...с вероятностями

Р (Х = m)= р(1-р)^m-1 (m = 1,2,3...) р = const

1 2 … m … 1

(X=m)=( ) S= -

P pq … pq^m-1 … q-1

∞ ∞ ∞ ∞ 1

MX= Σ mpq^m-1= p Σ mq ^m-1 = p Σ (q^m)_q = p(Σ q^m) _q =p ( - ) _q =

^{m=1 m=0 m=0 m=0} 1-q

1 p

= p – = - = -

(1-q)² p² p

DX = М(Х²)-(МХ)²

∞ ∞ ∞ ∞

М(Х²)= Σ m²pq ^m-1 = Σ m(m-1+1)pq ^m-1 = Σ m(m-1)p q ^m-1 + Σ p q ^m-1

^{m=0 m=0 m=1 m=1}

∞ ∞ 1 q 1-p

DX= Σ m(m-1)p q ^m-1 + Σ p q ^m-1 - - = - = -

^{m=1 m=1} p² p² p²

Вывести выражение для дисперсии случайной величины, распределенной по геометрическому закону.

СВ Х называется распределенной по геометрическому закону с параметром р ( где р? [0;1]), если она принимает значения 1, 2,3 ...с вероятностями

Р (Х = m)= р(1-р)^m-1 (m = 1,2,3...) р = const

1 2 … m … 1

(X=m)=( ) S= -

P pq … pq^m-1 … q-1

∞ ∞ ∞ ∞ 1

MX= Σ mpq^m-1= p Σ mq ^m-1 = p Σ (q^m)_q = p(Σ q^m) _q =p ( - ) _q =

^{m=1 m=0 m=0 m=0} 1-q

1 p

= p – = - = -

(1-q)² p² p

DX = М(Х²)-(МХ)²

∞ ∞ ∞ ∞

М(Х²)= Σ m²pq ^m-1 = Σ m(m-1+1)pq ^m-1 = Σ m(m-1)p q ^m-1 + Σ p q ^m-1

^{m=0 m=0 m=1 m=1}

∞ ∞ 1 q 1-p

DX= Σ m(m-1)p q ^m-1 + Σ p q ^m-1 - - = - = -

^{m=1 m=1} p² p² p²

Числовые характеристики случайных величин, распределенных по биномиальному, геометрическому закону и закону Пуассона (значения мат. ожидания и дисперсии)

Биноминальный закон

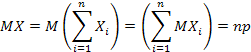
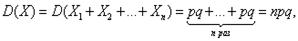
Геометрический закон

=

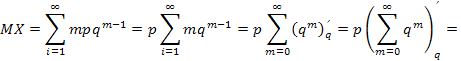
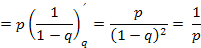
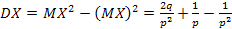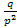
Закон Пуассона