Вращательное движение твердого тела. Скорость и ускорение точек тела

Модуль скорости точки тела, отстоящей отоси вра­щения на расстоянии h, определяют по формуле

v = |ω| h . (34)

Ускорение любой точки тела равно сумме центростре­мительного и вращательного ускорений:

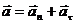, (35)

где

a_п = ω²h, a_τ = |ε| h. (36)

Вектор 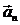всегда направлен по перпендикуляру к оси вращения (в сторону оси), вектор 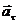направлен по касательной к траектории точки в ту же сторону, что и ско­рость, если вращение тела ускоренное, и в обратную, если оно замедленное.

Модуль ускорения находят по формуле

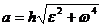. (37)

Острый угол между 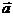и

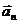
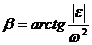. (38)

Пример 2.При наличии крутильных колебаний вра­щение вала описывается уравнением φ = ω₀t + φ₀sin kt, где (φ₀, ω₀, k - постоянные. Определить модули скорости, касательного и нормального ускорений точки вала, если ее расстояние до оси вала равно r.

Решение. Определим угловую скорость и угловое ускорение вала по (26) и (27):

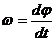= ω₀+ φ₀ k cos kt, 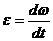= - φ₀ k²sin kt.

Найдем модуль скорости точки по формуле (34);

v = |ω| r =|ω₀+ φ₀ k sin kt| r.

Максимальный модуль этой скорости будет достигаться в те мо­менты времени, для которых cos kt = 1, т. е.

v_max = (ω₀+ φ₀ k)r.

Найдем модуль нормального ускорения по (36):

а_п = ω²t =(ω₀+ φ₀ k sin kt)²r.

Оно имеет максимум одновременно со скоростью, следовательно,

(а_n)_тах= (ω₀ + φ₀ k)²r

Определим модуль касательного ускорения

a_τ = |ε| r = φ₀ k² r |sin kt|.

Максимальное значение его (a_τ)_max = φ₀ k².

Задачи

Задача 1.3.22.* По проекту Циолковского, для создания искусственной тяжести на обитаемых искусственных спут­никах, имеющих форму кольца (тора), предполагается им сообщить вращательное движение вокруг оси симметрии. Определить период такого вращения, необходимый для того, чтобы находящиеся на нем тела имели земной вес, если их расстояния до оси вращения равны 39,2 м (g = 9,8 м/с²).

Ответ: Т = 4π с.

1.3.23.* Для безопасной работы маховика необхо­димо, чтобы ускорения его точек не превосходили некоторого предельного значения а_mах. Определить предельное значение угловой скорости, считая ее постоянной, если радиус маховика равен R.

Ответ: ω_max= .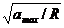

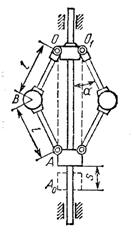
Рис. 40 Рис. 41

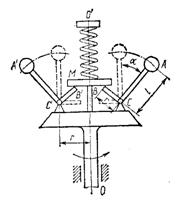
1.3.24.* На какое расстояние s = A₀A переместилась муфта А регулятора (рис. 40), если известно, что ускорение центра каждого шара В равно 288 м/с², угло­вая скорость регулятора постоянна и равна 60 рад/с, а A₀ - положение муфты при α = 0. Длины стержней 10см. Рас­стоянием OO₁ пренебречь.

Ответ: s = 8 см.

1.3.25.*В центробежном регуляторе (рис. 41) при вращении вокруг вертикальной оси ОО₁ рычаги АВС и A'C'B' поворачиваются вокруг горизонтальных осей С и С' и отжимают муфту М. Зная перемещение муфты s, длины плеч рычагов: BC= B'C' = r; AC = A'C' = 1 и угловую скорость регулятора ω = const. определить модули ускорений шаров А и А'. При отсутствии вращения ВС и В'С' перпендикулярны оси OO', а АС и А'С' параллельны этой оси. Расстояние СС' = 2b.

Ответ: .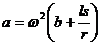

1.3.26.* Корабельный зубчатый редуктор (рис. 42) состоит из трех зубчатых колес. Первое колесо диамет­ром 20 см делает 7200 об/мин. Второе колесо делает 4000 об/мин, а третье, вращающее гребной вал, совершает 600 об/мин. Определить диаметры второго и третьего колес.

Ответ: d₂ = 36 см; d₃ = 240 см.

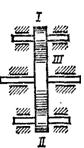
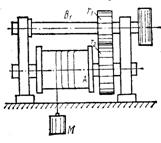
Рис. 42 Рис. 43

11.3.27.*На барабан А радиусом R=15 см одноступен-чатого зубчатого редуктора лебедки (pис. 43) намотан трос, на конце которого подвешен груз М. В течение 5 с грузподнимается с постоянным ускорением а₀= 0,2π м/с². Определить, сколько оборотов сделает ведущий вал В₁ за этот промежуток времени, если начальная скорость груза v₀ = 0,1π м/с, радиус ведущей шестерни r₁ = 10cм, а ведо­мой r₂ = 20 см.

Ответ: 20 оборотов.

1.3.28.* Диск вращается вокруг неподвижной оси в течение некоторого промежутка времени так, что уско­рения всех его точек состав­ляют с их скоростями одина­ковые углы, равные 45°. Оп­ределить угловую скоростьдиска как функцию времени, если в момент t = 0 она была равна ω.

Ответ: 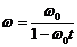(для t < 1/ω₀c).

1.3.29.*Вращение твердого тела вокруг неподвиж­ной оси задано уравнением φ = 1,5t² - 4t (φ - в радианах, t - в секундах). Определить: 1) ха­рактер вращения тела в моменты t₁= l с и t₂ = 2 с; 2) модули скоро­сти и ускорения точки тела, отстоя­щей от оси вращения на расстоянии 0,2 м, в эти моменты времени.

Ответ: 1) при t = 1 с вращение замедленное; при t₂ = 2 с вращение ускоренное;

2) v₁ = 0,2 м/с; а₁= 0,633 м/с²; v₂ = 0,4 м/с; a₂ = 1,0м/с².

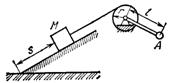1.3.30.* Груз М поднимается по наклонной плоскости с помощью ворота (рис. 44) так, что проходи­мое им расстояние s = 2πt³ см. Оп­ределить модули скорости и ускорения конца рукоятки А после од­ного оборота, если радиус барабана r = 27 см, а

Рис. 44 длина рукоятки l = 54 см.

Ответ: v = 3,39 м/с, а = 21, 3м/с².

1.3.31.* Вращение винта корабля в период пуска задано уравнением φ =15π + 3070(e^-kt - 1) (k - величина постоянная). Определить наибольшую угловую скорость винта (об/мин), а также модуль ускорения точки, отстоящей от оси винта на расстоянии 0,8 м, в момент t= 0, если на­чальная угловая скорость винта равна нулю. Определить также момент времени t, когда винт будет делать 270 об/мин.

Ответ: n_max = 450 об/мин; а|_t=0 = 0,58 м/с²; t = 60 с.

1.3.32.* Стержень АВ (рис. 45), двигающийся вниз

в вертикальных направляющих с постоянной скоростью v,

скользит своим концом В по стороне CD прямоугольного рычага CDO, благодаря чему последний 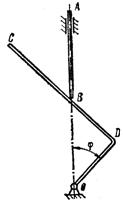поворачивается вокруг точки О, лежащей на оси направляющей. Опреде­лить модули скорости и ускорения точки С рычага в за­висимости от угла поворота φ, если OD = b; CD = 2b. Ответ: ;

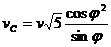Рис. 45 .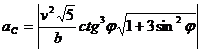

1.3.33. Тело вращается вокруг неподвижной оси согласно закону φ = t². Определить скорость точки тела на расстоянии r = 0,5 м от оси вращения в момент времени, когда угол поворота φ = 25 рад. (5)

1.3.34. Тело вращается равнопеременно с угловым ускорением ε = 5 рад/с². Определить скорость точки на расстоянии r = 0,2 м от оси вращения в момент времени t = 2с, если при t₀ =0 угловая скорость ω₀= 0. (2)

1.3.35. Груз 1 (рис. 46) поднимается с помощью лебедки, барабан 2 которой вращается согласно закону

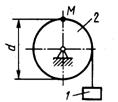φ = 5 + 2t³. Определить скорость точки М барабана в момент времени t = 1 с, если диа­метр d = 0,6 м. (1,8)

1.3.36. Угловая скорость балансира механических часов изменяется по закону ω = π sin 4 π t.

Рис. 46 Определить в см/с скорость точки балансира на расстоянии h = 6 мм от оси вращения в момент времени t = 0,125 с. (1,88)

1.3.37. Скорость точки тела на расстоянии r = 0,2 м от оси вращения изменяется по закону v = 4t². Определить угловое ускорение дан­ного тела в момент времени t = 2с. (80)

1.3.38. Маховик вращается с постоянной частотой вращения, равной 90 об/мин. Определить ускорение точки маховика на расстоянии 0,043 м от оси вращения. (3,82).

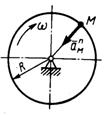1.3.39. Тело вращается вокруг неподвижной оси согласно закону φ = 2t². Определить нормальное ускорение точки тела на расстоянии r = 0,2 м от оси вращения в момент времени t = 2 с. (12,8)

1.3.40. Нормальное ускорение точки М диска, вращающегося вокруг неподвижной оси (рис. 47), рав­но 6,4 м/с².Определить угловую скорость ω этого диска, если его радиус R = 0,4 м.

Рис. 47 (4)

1.3.41.Тело вращается вокруг неподвижной оси согласно закону φ = 2t³. В момент времени t = 2 с

определить касательное ускорение точки тела на расстоянии от оси вращения r = 0,2 м. (4,8)

1.3.42. Угловая скорость тела изменяется по закону ω = 2t³. Опре­делить касательное ускорение точки этого тела на расстоянии r = 0,2 м от оси вращения в момент времени t = 2 с. (4,8)

1.3.43. В данный момент времени ротор электро-двигателя вращаетcя с угловой скоростью ω = 3 π и угловым ускорением ε = 8 π. Определить ускорениеточки ротора на расстоянии 0,04м от оси вращения .(3,69)

1.3.44. Тело вращается согласно закону φ = 1 + 4t. Определить ускорение точки тела на расстоянии r = 0,2 м от оси вращения. (3,2)

1.3.45. Угловая скорость тела изменяется по закону

ω=1+t. Опреде­лить ускорение точки этого тела на расстоянии r = 0,2 м от оси вра­щения в момент времени t = 1 с. (0,825)

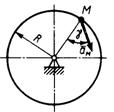1.3.46. Маховое колесо в данный момент времени вращается с угловым ускорением ε = 20 π, а его точка на расстоянии от оси вращения 5 см имеет ускорение a = 8 π. Определить нормальное ускорение указаннойточки. (24,9)

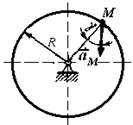1.3.47.Ускорение точки М диска (рис.48), вращающегося вокруг неподвижной оси, равно 4 м/с².

Рис. 48 Определить угловую скорость этого диска, если его радиус R = 0,5 м, а угол γ = 60°. (2)

1.3.48.Ускорение точки М диска, вращающегося вокруг неподвижной оси (рис. 49), равно 8 м/с². Определить угловое ускорение этого диска, если его радиус R = 0,4 м, а

Рис. 49 угол γ = 30°. (10)

1.3.4. Преобразование поступательного и вращательного движения тела в механизмах

1.3.49.При движении клина по горизонтальным направляющим со ско­ростью 1 м/с другой клин перемещается в вертикальном направлении со скоростью 1 м/с. Определить угол в градусах скоса клиньев. (45)

1.3.50. Клинья 1 и 3 перемещаются по параллель­ным горизонтальным направляющим, а проме­жуточный клин 2 - по вертикальным направ­ляющим (рис.50). Определить перемещение клина 3, если перемещение клина 1 равно 0,12 м, а угл α = 30° и β = 60°. (0,04)

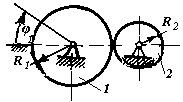1.3.51. Колесо 1 (рис. 51) вращается согласно закону φ₁=20t. Определить число оборотов, совершен­ных коле-сом 2 за время t = 3,14 с, если ради­усы колес R₁ = 0,8 м, R₂ = 0,5 м. (16)

Рис. 50 Рис. 51

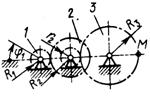
1.3.52. Зубчатое колесо 1 (рис. 52) вращается равнопере­менно с угловым ускорением ε₁ = 4 рад/с². Определить скорость точки М в момент вре­мени t = 2 с, если радиусы зубчатых колеc R₁= 0,4 м, R₃ = 0,5 м. Движение начинается из состояния покоя. (3,2)

Рис. 52 Рис.53

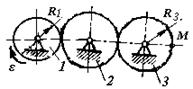
1.3.53. Зубчатое колесо 1 (рис. 53) вращается согласно закону φ₁ = 4 t² . Определить скорость точки М колеса 3 в момент времени t =2с, если радиусы колес R₁= 0,4 м, R₂= 0,8 м, r₂ = 0,4 м, R₃ = 1 м. (3,2)

1.3.54.Редуктор (рис. 54) состоит из конической и цилинд­рической зубчатых передач с числом зубьев колес z₁ = 18, z₂ = 26, z₃ = 28 и z₄ = 40. Вал 1 вращается с угловой скоростью ω = 20 (t + e^-t). В момент времени t = 10 с опре­делить угловую скорость вала 2. (96,9)

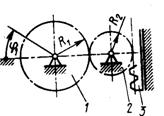
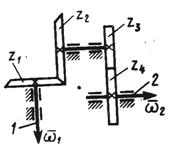
Рис.54 Рис. 55

1.3.55.Зубчатое колесо 1 (рис. 55) вращается согласно закону φ₁= 4t². Определить ускорение рейки 3, если радиусы зубчатых колес R₁ = 0,8 м, R₂= 0,4 м. (6,4)

1.3.56.Вариатор (рис. 56) состоит из ведущего диска 1, ролика 2 и ведомого диска 3. Угловые скорости дисков ω₁= 10 рад/с, ω₂ = 5 рад/с. Опреде­лить отношение расстояний b/d. (2)

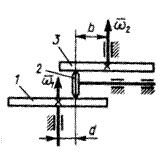
Рис. 56 Рис. 57

1.3.57. Груз 1 поднимается с помощью лебедки 2 (рис. 57). Закон движения груза имеет вид: s = 7 + 5 t², где s - в см. Определить угловую скорость барабана в момент времени t = 3 с, если его диаметр d = 50 см. (1,2)

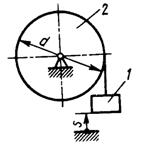
1.3.58. Какой должна быть частота вращения (об/мин) п₁ шестерни 3 (рис. 58), чтобы тело 1 двига­лось с постоянной скоростью v = 90 см/с, если числа зубьев шестерен z₃ = 26, z₂ = 78 и ра­диус барабана r = 10 см? (258)

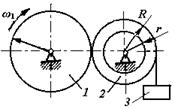
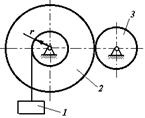
Рис.58 Рис. 59

1.3.59.Угловая скорость зубчатого колеса 1 (рис. 59) из­меняется по закону ω₁ = 2t². Определить ус­корение груза 3 в момент времени t = 2 с, если радиусы шестерен R₁ = 1 м, R₂ = 0,8 м и радиус барабана r = 0,4 м. (4)

1.3.60.Зубчатое колесо 3 (рис. 60) вращается равнопере­менно с угловым ускорением ε₃= 8 рад/с². Определить путь, пройденный грузом 1 за про­межуток времени t =3 с, если радиусы R₂=0,8 м, R₃=0,6 м, r =0,4 м. Груз 1 в начале движения находился в покое. (10, 8)

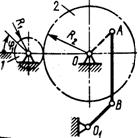
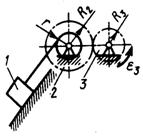
Рис. 60 Рис. 61

1.3.61.Зубчатое колесо 1 (рис. 61) вращается согласно закону φ = 2t³. Определить скорость точки В в момент времени t = 2 с, если радиусы ко­лес R₁ = 0,3 м, R₂ = 0,9 м, длина кривошипа O₁B =ОА = 0,6 м, расстояние 00₁ = АВ. (4,8)

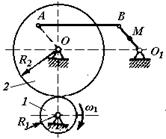1.3.62. Зубчатое колесо 1 (рис. 62) вращается равномер-но с угловой скоростью ω₁ = 6 рад/с. Определить ускорение точки М, если радиусы колес R₁ = 0,3 м, R₂ = 0,9 м, расстояние О₁М = 0,3 м. ОА = O₁B и AB = OO₁. (1,2)

Рис.62

1.4. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА