Уравнение движения точки по траектории имеет вид

s = s(t), (10)

где s - дуговая координата, отсчитываемая от выбранного начала отсчета на траектории. Знак s определяют в соот­ветствии с выбранным направлением отсчета дуг.

При задании движения точки естественным способом ее скорость находят по формуле

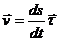, (11)

где 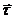-единичный вектор касательной, направленный в сторону возрастающих значений дуговой координаты s.

Скорость точки как алгебраическую величину опреде­ляют по формуле

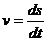. (12)

При v > 0 точка движется в сторону возрастающих, а при v < 0 - в сторону убывающих значений s.

Если известна зависимость v = v(t), то дуговую коор­динату находят по формуле

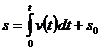, (13)

где s₀ - значение дуговой координаты при t = 0.

Если начало отсчета дуг совпадает с начальным по­ложением точки, то s₀ = 0, и тогда

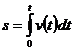. (14)

Так как движущаяся точка может изменить направле­ние движения по траектории, то путь σ, пройденный точкой за промежуток времени (0, t), определяют как сумму длин дуг отдельных участков, на каждом из ко­торых скорость v сохраняет свой знак.

Таким образом,

σ = |s₁ - s₀| + |s₂ - s₁| + ... + |s - s_n|. (15)

где s₁, s₂, .... s_п - значения дуговой координаты в мо­менты времени t₁, t₂,…t_n,в которые скорость v изменяет свой знак.

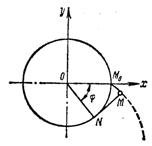Пример 1. Не­растяжимый трос сматывается с неподвижного барабана ра­диусом R, все время оставаясь в натянутом состоянии (рис. 20). Опре­делить уравнение движения по траектории точки троса, нахо­дившейся в начальный момент времени на барабане, если угол φ, определяющий положение ра­диуса, проведенного в точку Nсхода троса, задан каквозрастающая функция времени(φ > 0).

Решение. Проведем ось Ох через центр барабана и начальное положение рассматриваемой точки

Рис. 20 М_у. В силу нерастяжимости троса длина смотанного конца равна длине соответствующей дуги бара­бана, т. е. NM = 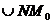= Rφ.

Из рисунка найдем

X = ON cos φ + NM sin φ = R cos φ + Rφ sin φ;

y = - ON sin φ + NM cos φ= - R sin φ - Rφ cos φ.

При сматывании троса угол φ = φ(t), следовательно, эти уравнения являются уравнениями движения точки М.

Найдем проекции скорости точки на выбранные оси:

;

,

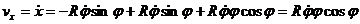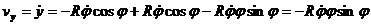следовательно,

.

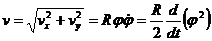Считая, что φ = 0, s = 0 при t = 0, по формуле (14) найдем

.

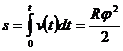Если вместо φ подставить известную функцию φ = φ(t), то

,

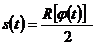т. е. получим уравнение движения точки по траектории.

Пример 2. Движение точки по траектории задано уравнением 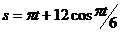(s - в метрах, t - в секундах). Определить значение дуговой координаты s в момент t = 15 с и путь σ, пройденный точкой за первые 15 с.

Решение. Определим скорость точки

.

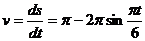Найдем моменты времени t₁, t_2,…, в которые скорость точки изменяет свой знак:

,

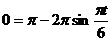откуда t_n+1 = (-l)ⁿ +6n с (п = 0;1; 2; ...).

Следовательно, в течение первых 15 с скорость изменяет свой знак в моменты времени: t₁= l с, t₂ = 5 с, t₃ = 13 с.

Определим значения дуговой координаты s вэти моменты вре­мени, а также в момент

t₀ = 0 и в момент t₄ = 15 с:

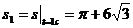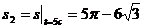s₀ = 12 м;

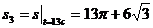м;

м;

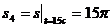м;

м.

Пользуясь формулой (15), найдем путь, пройденный точкой за первые 15 с:

П = |π+6√З-l2| + |5π-6√3-π-6√3| + |13π+6√3-5π+6√3 | +

+|15π-13π-6√3| = 59,7 м.

Пример 3. Определить уравнение движения точки по траектории, если даны ее уравнения движения в декар­товых координатах:

х = а (2 cos t + cos 2t), y = a(2sin t—sin 2t), 0 ≤ t ≤ .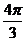

Дуговую координату отсчитывать от начального по­ложения точки в сторону первоначального движения.

Решение. Заданные уравнения представляют собой параметриче­ские уравнения гипоциклоиды, т. е. линии, которую описывает точка окружности радиусом а, катящейся внутри окружности радиусом 3а, причем t равно углу поворота линии центров от ее начального по­ложения.

Для определения s найдем v(t):

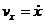= - 2а (sin t + sin 2t),

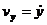= 2a (cos t - cos 2t),

отсюда .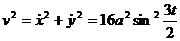

Заметим, что величина v(t) всегда положительна, так как точка не меняет направления своего движения. Это следует из вышеука­занной интерпретации движения. Аналитически в этом можно убе­диться, если рассмотреть изменение угла φ, образованного радиус-вектором точки с осью абсцисс:

tg φ = x/y; φ = arc tg x/y,

отсюда

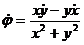
Знаменатель и числитель всегда положительны, так как

.

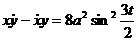Таким образом, точка всегда движется в одном направлении (φ растет) и скорость сохраняет постоянный знак, который совпадает с ее первоначальным знаком:

.

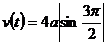Для s(t) получим

.

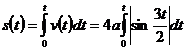Этот интеграл не может быть вычислен в элементарных функциях (для произвольного t). Вычислим его по участкам.

При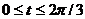

,

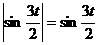тогда s(t)= .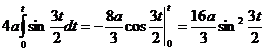

В частности, при t = 2π/3

s = (2π/3) = 16a/3.

Применять эту формулу при больших t нельзя. Например, при t = 4π/3 она привела бы к нелепому результату s = 0. При , .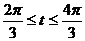

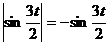Тогда

.

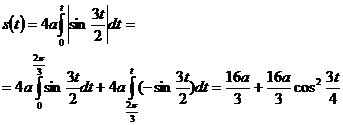Задачи

1.2.1.* Определить уравнение движения точки по траектории, а также значение дуговой координаты s и пройденный путь σ к моменту t = 5с, если ее скорость v задана уравнением:

1) v =10 см/с;

2) v = 2 см/с (0 ≤ t ≤ 3);

v = (5 - t) см/с(3 ≤ t ≤ 5);

3) v = (2t+1) см/с;

4) v = (3 - t) см/с;

5) v = 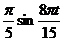см/с;

6) см/с;

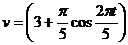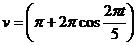7) см/с;

8) v = (t² - 3t + 2) см/с.

Ответы:

1) s = 10t см; s|_t=5c = 50 см; σ|_t=5c = 50 см;

2) s = 2t см (0 ≤ t ≤ 3); s = (5t - 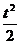- 4,5) см (3 ≤ t ≤ 5);

s|_t=5c = 8 см; σ|_{t=5 c}= 8 см;

3) s = (t² + t) см; s|_t=5c = 30 см; σ|_t=5c = 30 см;

4) s =(3t - 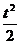) см; s|_t=5c = 2,5 см; σ|_t=5c = 6,5 см;

5) s = 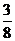(1- cos 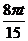) см; s|_t=5c = 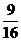см; σ|_t=5c = 2 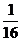см;

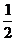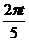6) s = (3t + sin ) см; s|_t=5c = 15 см; σ|_t=5c = 15см;

7) s = (πt +5 sin 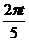) см; s|_t=5c = 5π см;

σ|_t=5c = 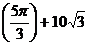см;

8) s = 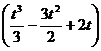см; s|_t=5c = 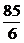см; σ|_t=5c = 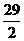см.

1.2.2.*Определить уравнение движения точкипотраектории, если даны уравнения ее движения в декарто­вых координатах. Дуговую координату s отсчитывать от начального положения точки в сторону первоначального движения:

1) x = Зt² + 5; y = 4t² + 3;

2) x = 1 – t; y = t - 1;

3) x = 2sin 2t; y = 2cos 2t;

4) x = a+r cos ωt; y = r sin ωt;

5 ) х = 3cos t²; y = 3sin t²;

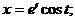
6) 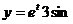; z = e^t;

7) x = 4a cos²ωt; y = За sin²ωt;

8) x = acos³t; y = a sin³t;

9) x = a(t - sin t ); y = a(l - cos t);

10) x = a cos t; у = a sint; z = ct.

Ответы: 1) s = 5t²;

2) s =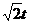

3) s = 4t;

4) s = rωt;

5) s = 3t²;

6) s = √3(e^t—l);

7) s = 5a sin²ωt;

8) s = 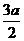sin²t [ 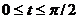(см. пример 3)];

9) s = 4a(l-cos 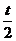) [ 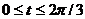(см. пример 3)];

10) .

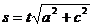1.2.3.* Колесо радиусом R катится без скольже­ния по горизонтальному рельсу со скоростью центра 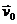. Определить уравнение движения по траектории точки обода колеса, находившейся в начальный момент в точке каса­ния с рельсом. Какое расстояние s_i будет пройдено точ­кой по траектории от начала движения до наивысшего положения?

Ответ: s = 8R sin² 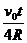; s_i = 4R. Выражение для s справедливо только до момента t = 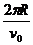, при котором s = 8R. После него нужно вычис­лять s так же, как в примере 3.

1.2.4. Точка движется по траектории согласно уравнению s = 15 + 4 sin πt. Указать ближайший после начала движения момент вре­мени t₁, при котором s₁=17 м. (0.167)

1.2.5. Точка движется по траектории согласно уравнению s = 0,5t² + 4t. Определить, в какой момент времени скорость точки дос­тигнет 10 м/с. (6)

1.2.6. Точка движется по заданной траектории со скоростью v = 5 м/с. Определить криволинейную координату s точки в момент времени t = 18 с, если при

t₀ = 0 координата s₀ = 26 м. (116)

1.2.7. Точка движется по кривой со скоростью v = 0,5 t. Определить ее координату в момент времени t = 10 с, если при t₀ = 0 координатa точки s₀ = 0. (25)