Применение искусственных базисных неизвестных к решению основной задачи ЛП. Условие противоречивости системы условий исходной задачи.

Метод искусственного базисаприменяется к решению задач линейного программирования в общем случае, когда система ограничений не имеет предпочитаемого вида.

Пусть требуется минимизировать 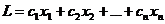(1) при ограничениях:

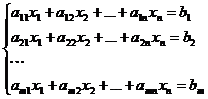(2)

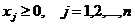. (3)

К данной задаче ЛП непосредственно нельзя применить симплексный метод, т.к. система (2) не имеет предпочитаемого вида, хотя правые части всех ее уравнений можно считать неотрицательными. Поэтому к левой части каждого уравнения системы (2) добавим по одной искусственной неотрицательной неизвестной и образуем следующую систему m линейных уравнений с n+m неизвестными:

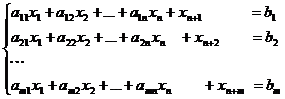(4)

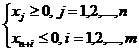где (5)

Очевидно, в системе (4) неизвестные 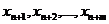образуют базисный набор, который принято называть искусственным. Кроме того, образуем искусственную линейную форму: 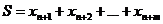(6) и сформулируем следующую вспомогательную задачу линейного программирования: минимизировать линейную форму (6) при линейных ограничениях (4) и (5).

Для решения вспомогательной задачи можно применить симплексный метод, так как система (4) имеет предпочитаемый вид, искусственные неизвестные 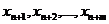являются базисными, а правые части всех уравнений неотрицательны. В процессе решения вспомогательной задачи система уравнений (4) будет подвергаться симплексным преобразованиям, в результате которых искусственные базисные неизвестные будут переходить в число свободных, а в базисный набор будут постепенно включаться исходные неизвестные. На некотором этапе процесса решения вспомогательной задачи система уравнений (4) примет такой предпочитаемый вид, что соответствующее базисное решение будет оптимальным решением этой задачи. При этом минимальное значение целевой функции может быть или положительным, или равным нулю, так как функция представляет сумму неотрицательных переменных.

Если S_min<0, то исходная задача не имеет решения ввиду противоречивости условий (2) и (3). Действительно, если допустить, что система уравнений (2) имеет неотрицательное решение (α₁,α₂,...,α_n), то вспомогательная задача будет иметь решение (α₁,α₂,...,α_n,0,0,…,0) для которого S=0, что противоречит предположению.

Если же S=0, то возможна дальнейшая минимизация.

В каком случае процесс решения задачи ЛП симплекс-методом является конечным.

Один шаг симплекс-метода состоит в работе с конкретным базисным решением и заключается в следующем:

1)вычисляется симплекс-разности для всех свободных переменных:

c_j-c_Bq_j , j=m+1, m+n;

2)определяется максимальная симплекс-разность

c_s –c_Bq_s =max (c_j- c_Bq_j )

m+1≤j≤m+n

(если разность положительна,переходим к след пункту,если нет то алгоритм закончен)

3)в базис вводится переменная Хs, а выводится переменная Xr, для которой

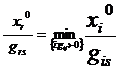
Эти шаги повторяются до тех пор,пока на некотором шаге все симплекс-разности станут неположительными.Тогда оптимальное решение получено.