Дайте определение матрицы, обратной квадратной матрице А. Какое условие является необходимым и достаточным условием существования обратной матрицы?

Дайте определение матрицы, обратной квадратной матрице А. Какое условие является необходимым и достаточным условием существования обратной матрицы?

Пусть задана кв. матрица А.Если сущ-т матрица В, такая что А*В=Е,то гов что матрица В явл обратной по отношению к мат А: В=А^-1, А*А^-1=Е.

Свойства: 1)Обратная и исходная матрицы перестановочны и матрица,обратная обратной, совпадает с исходной:

А*А^-1=А^-1*А=Е.

2)Единственность матрицы: если для данной матрицы обратная мат сущ-т,то она только одна.

Как выяснить явл ли кв. матрица обратной? Пусть исход матрица А имеет вид: а₁₁ а₁₂ а₁₃

А= а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

Предпол что имеется какая-то мат В, В=(х_ij)=А^-1,кот явл обратной по отношению к исходной мат-це А. Тогда должно выполняться:

а₁₁ а₁₂ .. а_1n x₁₁ x₁₂ .. x_1n 10….0

а₂₁ а₂₂ .. а_2n * x₂₁ x₂₂ .. x_2n = 010...0

…………… ………….. …….

а₃₁ а₃₂ .. а_3n x_m1 x_m2 .. x_mn 000001

Это матричное ур-е можно переписать в виде системы n² линейных ур-й с n² неизвестными.

3)Квадратная матрица обратима тогда и только тогда, когда она является невырожденной.

5.СЛАУ решается методом Жордана- Гаусса. Каким образом в процессе решения убедиться в том, что СЛАУ:

Не имеет решения?

Имеет уравнение, являющееся линейной комбинацией каких-либо других уравнений системы?

Суть метода состоит в том, что за счёт элементарных преобразований, за конечное число шагов система приводится к так называемому, предпочитаемому или каноническому виду, кот легко исслед-ся и решается. Выбирается разрешающее ур-е, в кот выбирается неизвестная, коэф-т при кот отличен от нуля (разреш-ая неизвестная), а коэф-т при ней назыв разрешающий коэф-т. Путём элем-х преобразований разреш-ая неизвестная искл-ся из всех урав-й системы кроме разрешающей. Берётся след ур-е и след разреш-ая перем-ая отличная от первой, далее путём элем-х преобр-й она искл-ся из всех ур-й системы кроме разрешающей и т.д. Пример:

а₁₁х₁+а₁₂х₂+а_1nх_n=b_{1 –} разреш урав-е

а₁₁¹0 а_m1х₁-разреш перем-ая

нужно искл х₁ из всех ур-й кроме разрешающего. Нужно 1-е ур-е умножить на (-а₂₁/а₁₁)=>

-а₂₁х₁- а₁₂*а₂₁/а₁₁*х₂ -…- а₂₁*а_1n/а₁₁*х_n=-b₁*а₂₁/а₁₁ + 2 ур-е системы

В рез-те преобр-й возможны след.случаи:

1) в процессе реш-я появл равенства 0*х₁+0-х₂+…+0-х_n=b_i в_i¹0

при появл такого равенства пишем что сис-ма несовместна.

2) левая и правая части i ур-я обращ-ся в 0, т.е.0=0 Þ данное ур-е явл линейной комбинацией ур-й вход-х в эту систему, в этом случае это ур-е исключается из всей системы

3) После того как будут получены решения системы, либо будет доказана её несовместность, система будет приведена к следующему виду:

х₁ + q_1,m+1*x_m+1 + … + q_1n*х_n=h₁

х₂ + q_2,m+1*x_m+1 + … + q_2n*х_n=h₂

_. . . . . . . . . . . . . . .

х_m + q_m,m+1*x_m+1 + … + q_mn*х_n=h_m

В этом случае говорят, что СЛАУ приведена к предпочитаемому или каноническому виду.

Единичная матрица: определение, формулы для элементов.

Матрица – это прямоугольная таблица чисел, содержащая m строк и n столбцов.

a₁₁ а₁₂ …а_1n

А= a₂₁ а₂₂ …а_2n или кратко А=(a_ij)

…………..

a_m1 а_m2 …а_mn

Если т=п, то матрица называется квадратной матрицей n-го по­рядка. Кв. матрица наз треугольной, если все ее элемен­ты, стоящие над или под главной диагональю, равны нулю. Кв. матрица называется диагональной, если все ее эл-ты, стоящие на главной диагонали, отличны от нуля, а остальные равны нулю. Диагональная матрица наз единичной, если у нее по главной диагонали стоят 1. Единичную матрицу принято обозначать буквой Е:

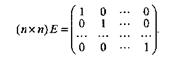
Основные понятия в теории графов: дуги, вершины в ориентированном и неориентированном графе. Примеры применения теории графов на практике.

Графом называется пара объектов, состоящая из множества точек и множества отрезков, соединяющих некоторые (может быть, все) из этих точек. Упомянутые точ-ки называются вершинами графа.

Если отрезки, соединяющие вершины графа, имеют направления, то граф называ-ется ориентированным, а сами отрезки — дугами. Если же отрезки не имеют направ-ления, то граф называется неориентированным, и в этом случае говорят, что вершины графа соединены ребрами. Смешанным называется граф, в котором содержатся как ориентированные, так и неориентированные отрезки. Ориентированный граф часто называют сетью.

Обозначим вершины графа 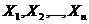, а дугу, соединяющую вершину X_i c X_j - u_ij.

Две дуги графа (два ребра) называются смежными, если они различны и имеют общую вершину. Две вершины графа называются смежными, если существует дуга (ребро), соединяющая их.

Говорят, что дуга исходит из вершины X_i, если X_i является ее началом. Дуга заходит в вершину X_j если X_jявляется ее концом.

Говорят, что в графе данная дуга инцидентна данной вершине, если эта вершина является началом или концом данной дуги.

Путь в ориентированном графе — это последовательность дуг, в которой конец предыдущей дуги совпадает с началом следующей. Путь, в котором ни одна вершина не встречается дважды, называется элементарным. Путь, в котором ни одна дуга не встречается дважды, называется простым, в противном случае — составным. Конечный путь, у которого конечная вершина совпадает с начальной, называется контуром. Контур, образованный одной дугой, называется петлей.

Ориентированный граф называется симметрическим, если любые две смежные вершины его соединены двумя противоположно ориентированными дугами. Ориентированный граф называется антисимметрическим, если каждая пара смежных вершин соединена только в одном направлении и петли отсутствуют.

20) Экономический смысл двойственной задачи к модели оптимального планирования производства. Математическая модель задачи определения расчетных оценок ресурсов.

Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях.

В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач.

Если система ограничений исходной задачи состоит из неравенств и на все переменные х_j наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.

Пусть исходная задача имеет вид: найти наибольшее значение функции

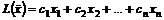
при ограничениях:

.

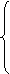
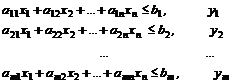
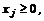
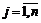Правило составления двойственных задач

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .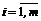

2. Составляется целевая функция 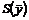, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

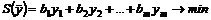. (1)

3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

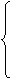
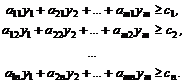₍₂₎

4. Переменные y_i в двойственной задаче также неотрицательны, т.е.

. (3)

Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.

В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.

Двойственные (расчетные) оценки ресурсов. Симметричная пара двойственных задач ЛП. Несимметричная пара двойственных задач ЛП, правила составления двойственной задачи для данной задачи ЛП со смешанными ограничениями.

Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях.

В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач.

Если система ограничений исходной задачи состоит из неравенств и на все переменные х_j наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.

Пусть исходная задача имеет вид: найти наибольшее значение функции

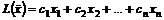
при ограничениях:

.

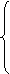
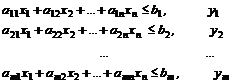
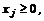
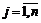Правило составления двойственных задач

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .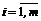

2. Составляется целевая функция 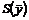, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

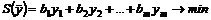. (1)

3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

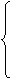
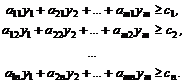₍₂₎

4. Переменные y_i в двойственной задаче также неотрицательны, т.е.

. (3)

Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.

В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.

39.Матричная запись пары двойственных задач ЛП (симметричная пара задач с ограничениями-неравенствами и нессиметричная пара,где в одной из задач ограничения имеют вид равенств)

Прямая Двойствен

AX≤И A*Y≥C

х≥0 Y≥0

F=CX=>max G=B*Y=>min

Если среди неравенств есть 1 равенство,то нессиметричная пара.

2х1+3х2+8х3≤50 у1

4х1-7х2+9х3=60 у2

40,41,42.Основное неравенство теории двойственности ЛП. Малая теорема двойственности и ее экономическое содержание. Теорема о достаточном условии оптимальности решений пары двойственных задач ЛП.

Для любых допустимых решени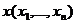й и 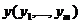прямой и двойственной задач ЛП справедливо неравенство: 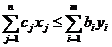. Для любого допустимого плана исходной задачи и для любого допустимого в-ра оценок ресурсов 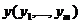общая стоимость всего произведенного продукта не превышает суммарной стоимости ресурсов.

Малая теорема двойственности: Для существования оптимального решения пары двойственных задач необходимо и достаточно существование допустимого решения для каждой из них.

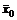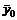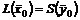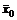Теорема о достаточном условии оптимальности решений пары двойственных задач: Если и - допустимые решения пары двойственных задач, для которых выполняется равенство , то и 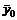- оптимальные решения соответствующих задач.

Согласно этой теореме, план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Постановка и математическая модель транспортной задачи,в которой суммарные запасы продукции меньше суммарныхъ запросов на нее.Записать правила сведения такой модели к замкнутой задаче и записать полученную замкнутую модель транспортной задачи.

Правило:Если суммарная мощность меньше суммарного спроса,то вводится фиктивный поставщик,его мощность=тому чего не хватает.В таблице вводится доп. строка,затраты считаются 0.

Постановка и математическая модель транспортной задачи,в которой суммарные запасы продукции больше суммарныхъ запросов на нее.Записать правила сведения такой модели к замкнутой задаче и записать полученную замкнутую модель транспортной задачи.

Правило:Если суммарная мощность меньше суммарного спроса,то вводится фиктивный потребитель,его мощность=тому чего не хватает.В таблице вводится доп. строка,затраты считаются 0.

Дайте определение матрицы, обратной квадратной матрице А. Какое условие является необходимым и достаточным условием существования обратной матрицы?

Пусть задана кв. матрица А.Если сущ-т матрица В, такая что А*В=Е,то гов что матрица В явл обратной по отношению к мат А: В=А^-1, А*А^-1=Е.

Свойства: 1)Обратная и исходная матрицы перестановочны и матрица,обратная обратной, совпадает с исходной:

А*А^-1=А^-1*А=Е.

2)Единственность матрицы: если для данной матрицы обратная мат сущ-т,то она только одна.

Как выяснить явл ли кв. матрица обратной? Пусть исход матрица А имеет вид: а₁₁ а₁₂ а₁₃

А= а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

Предпол что имеется какая-то мат В, В=(х_ij)=А^-1,кот явл обратной по отношению к исходной мат-це А. Тогда должно выполняться:

а₁₁ а₁₂ .. а_1n x₁₁ x₁₂ .. x_1n 10….0

а₂₁ а₂₂ .. а_2n * x₂₁ x₂₂ .. x_2n = 010...0

…………… ………….. …….

а₃₁ а₃₂ .. а_3n x_m1 x_m2 .. x_mn 000001

Это матричное ур-е можно переписать в виде системы n² линейных ур-й с n² неизвестными.

3)Квадратная матрица обратима тогда и только тогда, когда она является невырожденной.

5.СЛАУ решается методом Жордана- Гаусса. Каким образом в процессе решения убедиться в том, что СЛАУ:

Не имеет решения?