Золотая пропорция и тело человека
Древние скульпторы знали и использовали золотую пропорцию как критерий гармонии, канон красоты, корни которой лежат в пропорциях человеческого тела. “Человеческое тело – лучшая красота на земле”, - утверждал Н.Чернышевский. Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов: Фидия, Поликлета, Мирона, Праксителя. В создании своих творений греческие мастера использовали принцип золотой пропорции. Центр золотой пропорции строения человеческого тела располагался точно на месте пупка. И не случайно величину золотой пропорции принято обозначать буквой Ф; это сделано в честь Фидия – творца бессмертных скульптурных произведений.
Разработку теории пропорций человеческого тела в эпоху Возрождения начал Альбрехт Дюрер. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Pост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.
Художники, ученые, модельеры, дизайнеры делают свои расчеты ,чертежи или наброски исходя из соотношения золотого сечения. Леонардо Да Винчи создавал свои шедевры досконально изучив параметры человеческого тела и используя формулу золотой пропорции. Ле Корбюзье возводил свои архитектурные произведения, считающиеся шедеврами инженерной мысли также используя формулу Фибоначчи. Самая главная книга всех архитекторов – справочник Нойферта «Строительное проектирование» основано на параметрах туловища человека, заключающих в себе золотую пропорцию. Пропорции различных частей нашего тела составляет число очень близкое к золотому сечению. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы соотношение по данной схеме всегда равно золотому сечению. В строении черт лица человека также есть множество примеров приближающихся по значению к формуле золотого сечения. Наличие золотого сечения на лице и теле человека и есть идеал красоты. Если принять центром человеческого тела центр пупка , а расстояние от ступни человека до точки пупка за единицу измерения, то весь рост человека равен соотношению 1:1,618. Кроме того есть еще несколько основных золотых пропорций нашего тела. Соотношения расстояния от кончиков пальцев до локтя и от запястья до локтя равно отношению 1:1,618. Соотношения расстояния от уровня плеча до макушки головы = 1:1,618. Соотношение от точки пупка до макушки, от уровня плеча до макушки головы равно 1:1,618, от пупка до коленей и от коленей до ступней =1:1,618. Соотношение высоты лица и ширины лица =1:1,618 ,расстояние от бровей до центра губ и высоты носа=1:1,618, от макушки до подбородка и, от линии бровей до подбородка =1:1,168..соотношение ширины рта и ширина носа 1:1,618, соотношение ширины носа и ширины ноздрей, соотношение ширины между глазами и расстояния между бровями=1:1,618
Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.
ой сечение тело
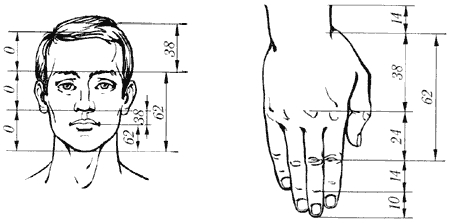
"Золотое сечение" и лицо человека.
Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется "динамической симметрией" или "динамическим равновесием". Какие же пропорции в лице человека стремятся к "золотому сечению"? Прежде всего, у людей с красивыми лицами наблюдается:
Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется "динамической симметрией" или "динамическим равновесием".
Соотношение высоты верхней и нижней губы будет 1,618:
Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38:
Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции "золотого сечения".
Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз - к ширине лба на уровне линии бровей, как все пропорции "золотого сечения".
Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка - как 38 : 62
Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию "золотого сечения"
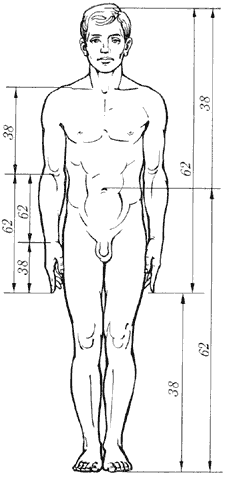
Пупок делит высоту человека в золотом отношении. Основание шеи делит расстояние от макушки до пупка в золотом отношении.
У большинства людей, верхняя точка уха делит высоту головы вместе с шеей в золотом отношении. Разделив в отношении золотого сечения отрезок, заключенный между макушкой и адамовым яблоком, мы получим точку, лежащую на линии бровей. Нижняя точка уха делит в золотом отношении расстояние от верхней части уха до основания шеи. Подбородок делит расстояние от нижней точки уха до основания шеи в золотом отношении
Человек – венец творения природы… Установлено, что золотые отношения можно найти и в пропорциях человеческого тела. Кроме того, человек сам является творцом, создаёт замечательные произведения искусства, в которых просматривается золотая пропорция. Человек, как и другие творения природы, подчиняется всеобщим законам развития. Корни этих законов нужно искать глубже - в строении клеток, хромосом и генов, а далее - в возникновении самой жизни на Земле.
Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется "динамической симметрией" или "динамическим равновесием". Какие же пропорции в лице человека стремятся к "золотому сечению"? Прежде всего, у людей с красивыми лицами наблюдается:
Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется "динамической симметрией" или "динамическим равновесием".
Соотношение высоты верхней и нижней губы будет 1,618:
Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38:
Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции "золотого сечения".
Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз - к ширине лба на уровне линии бровей, как все пропорции "золотого сечения".
Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка - как 38 : 62
Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию "золотого сечения"
Пупок делит высоту человека в золотом отношении. Основание шеи делит расстояние от макушки до пупка в золотом отношении.
У большинства людей, верхняя точка уха делит высоту головы вместе с шеей в золотом отношении. Разделив в отношении золотого сечения отрезок, заключенный между макушкой и адамовым яблоком, мы получим точку, лежащую на линии бровей. Нижняя точка уха делит в золотом отношении расстояние от верхней части уха до основания шеи. Подбородок делит расстояние от нижней точки уха до основания шеи в золотом отношении
Человек – венец творения природы… Установлено, что золотые отношения можно найти и в пропорциях человеческого тела. Кроме того, человек сам является творцом, создаёт замечательные произведения искусства, в которых просматривается золотая пропорция. Человек, как и другие творения природы, подчиняется всеобщим законам развития. Корни этих законов нужно искать глубже - в строении клеток, хромосом и генов, а далее - в возникновении самой жизни на Земле.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона.
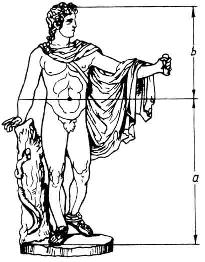
Как связано строение человеческого тела с числами Фибоначчи?
Числа Фибоначчи отражают основную закономерность роста организмов, следовательно, и в строении человеческого тела они должны каким – то образом проявиться.
Займемся “инвентаризацией” частей человеческого тела. У него одно туловище, одна голова, одно сердце и т. д.; многие части тела и органы парные, например: руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. У человека 12 пар ребер (одна пара атрофирована и присутствует в виде рудимента).
Характерно строение кисти человека. Кисть состоит из трех основных частей: запястья, пясти и пальцев. В состав запястья входит 8 косточек, оно сочленяется с 5 костями пясти, которые составляют основу ладони. Каждый палец состоит из трех фаланг: основных, средних и ногтевых. Позвоночник человека состоит из 34 позвонков.
Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34.
Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Действительно, как видно из рисунка отношение длины кисти и локтя к предплечью есть золотое сечение.
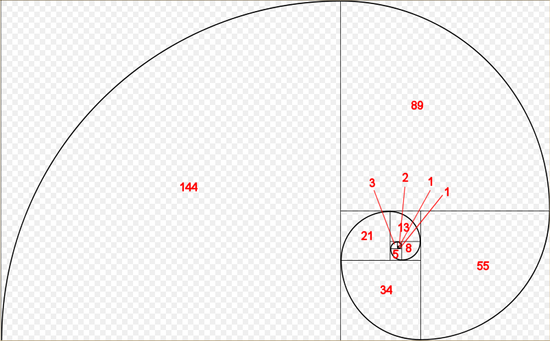
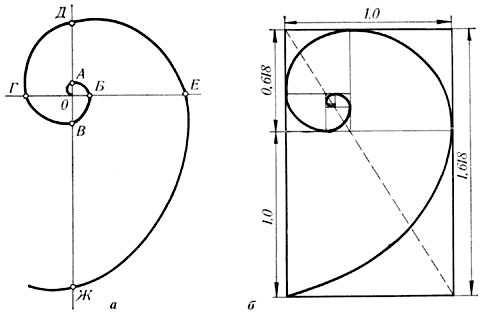
Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.

Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.
Выше мы уже писали о спиральности как характерной черте строения организмов. Оказалось. Что спиральность проявляется даже на клеточном уровне организации, в строении молекул живых организмов. Английский ученый Э. Синнот указывает в своих работах, что спиральность во многих случаях является отличительной особенностью протоплазмы; направления её движения в клетке тоже спиральное. Рост самих клеток тоже может быть спиральным. Не случайно носители генетической информации молекул ДНК и РНК построены по закону спирали. Советские ученые Б. Вайнштейн и Н. Киселев наблюдали, как белковые молекулы, полученые в результате “раздробления” вируса, снова собирались вместе в подходящих условиях и укладывались по правилу спирали. Естественно возникает вопрос: не здесь ли была заложена природой исходная информация спирального вида организмов?
Пропорции Фибоначчи в природе.
Просто удивительно, сколько постоянных можно вычислить при помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых. Приводимые ниже примеры показывают некоторые интересные приложения этой математической последовательности.
Раковина.
Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Cпирали очень распространены в природе. Раковина в форме спирали - форма раковины заинтересовала Архимеда и он выяснил, что увеличение длины завитков раковины – это постоянная величина и равна она 1,618.

Золотые" спирали широко распространены в биологическом мире. Рога баранов, коз, антилоп и других рогатых животных растут лишь с одного конца. Этот рост осуществляется по спирали.
И не только в раковине моллюска и рогах животных можно найти спирали Фибоначчи, а во многих цветах и растениях, просто они не такие явные.


