Переходные процессы. Классический метод расчёта переходных процессов

Переходные процессы. Классический метод расчёта переходных процессов

Классический метод расчета переходных процессов основан на составлении и последующем решении (интегрировании) дифференциальных уравнений, составленных по законам Кирхгофа и связывающих искомые токи и напряжения послекоммутационной цепи и заданные воздействующие функции (источники электрической энергии). Преобразуя систему уравнений, можно вывести итоговое дифференциальное уравнение относительно какой-либо одной переменной величины x(t):

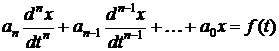. (4.2)

Здесь n – порядок дифференциального уравнения, он же – порядок цепи, коэффициенты a_k > 0 и определяются параметрами пассивных элементов R, L, C цепи, а правая часть является функцией задающих воздействий.

В соответствии с классической теорией дифференциальных уравнений полное решение неоднородного дифференциального уравнения находится в виде суммы частного решения неоднородного дифференциального уравнения и общего решения однородного дифференциального уравнения:

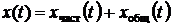. (4.3)

Частное решение полностью определяется видом правой части f(t) дифференциального уравнения. В электротехнических задачах правая часть зависит от воздействующих источников электрической энергии, поэтому вид 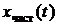обуславливается (принуждается) источниками электрической энергии и называется принужденной составляющей .

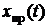Общее решение 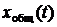однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части. В прикладных задачах электротехники 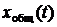не зависит (свободно) от воздействующих источников и по этой причине называется свободной составляющей 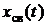и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.

Таким образом, любая искомая величина в переходном режиме

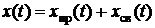. (4.3)

Свободную составляющую 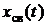переходного процесса ищут в виде

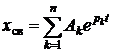, (4.4)

где n – порядок цепи, совпадающий с порядком дифференциального уравнения;

p_k – корни характеристического уравнения (собственные числа цепи);

A_k – постоянные интегрирования.

Собственные числа линейных цепей либо действительные отрицательные, либо комплексные с отрицательными вещественными частями (т.е. находятся в левой полуплоскости комплексных чисел). Поэтому 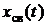носит преходящий (асимптотически затухающий до нуля) характер.

В искомом решении 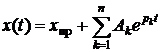надо уметь определять величины 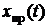, n, p_k, A_k.

Переходные процессы. Классический метод расчёта переходных процессов

Классический метод расчета переходных процессов основан на составлении и последующем решении (интегрировании) дифференциальных уравнений, составленных по законам Кирхгофа и связывающих искомые токи и напряжения послекоммутационной цепи и заданные воздействующие функции (источники электрической энергии). Преобразуя систему уравнений, можно вывести итоговое дифференциальное уравнение относительно какой-либо одной переменной величины x(t):

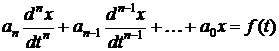. (4.2)

Здесь n – порядок дифференциального уравнения, он же – порядок цепи, коэффициенты a_k > 0 и определяются параметрами пассивных элементов R, L, C цепи, а правая часть является функцией задающих воздействий.

В соответствии с классической теорией дифференциальных уравнений полное решение неоднородного дифференциального уравнения находится в виде суммы частного решения неоднородного дифференциального уравнения и общего решения однородного дифференциального уравнения:

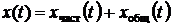. (4.3)

Частное решение полностью определяется видом правой части f(t) дифференциального уравнения. В электротехнических задачах правая часть зависит от воздействующих источников электрической энергии, поэтому вид 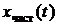обуславливается (принуждается) источниками электрической энергии и называется принужденной составляющей .

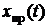Общее решение 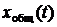однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части. В прикладных задачах электротехники 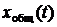не зависит (свободно) от воздействующих источников и по этой причине называется свободной составляющей 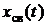и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.

Таким образом, любая искомая величина в переходном режиме

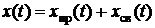. (4.3)

Свободную составляющую 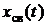переходного процесса ищут в виде

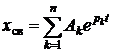, (4.4)

где n – порядок цепи, совпадающий с порядком дифференциального уравнения;

p_k – корни характеристического уравнения (собственные числа цепи);

A_k – постоянные интегрирования.

Собственные числа линейных цепей либо действительные отрицательные, либо комплексные с отрицательными вещественными частями (т.е. находятся в левой полуплоскости комплексных чисел). Поэтому 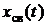носит преходящий (асимптотически затухающий до нуля) характер.

В искомом решении 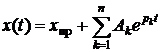надо уметь определять величины 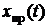, n, p_k, A_k.