Законы распределения функций случайных величин. Функция одного и двух случайных аргументов.

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = F_x (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

Функция распределения любой случайной величины обладает следующими свойствами:

• F(x)определена на всей числовой прямой R;
• F(x)не убывает, т.е. если x₁ 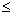x₂, то F(x₁) 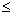F(x₂);
• F(- 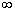)=0, F(+ 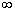)=1,т.е. 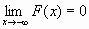и ;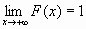
• F(x) непрерывна справа, т.е.

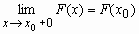
функция двух случайных аргументов:Если каждой паре возможных значений случайных величин и соответствует одно возможное значение случайной величины , то называют функцией двух случайных аргументов и и пишут:

Если и - дискретные независимые случайные величины, то для того, чтобы найти распределение функции , надо найти все возможные значения , для чего достаточно сложить каждое возможное значение со всеми возможными значениями ; вероятности же найденных значений равны произведениям вероятностей складываемых из значений и .

19. Закон больших чисел.теоремы закона больших чисел устанавливают зависимость между случайностью и необходимостью.

Закон больших чисел- это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.

Неравенство Чебышева.

Лемма: Если случайная величина Х имеет конечные математическое ожидание М(Х) и дисперсию Д(Х), то для любого положительного eсправедливо неравенство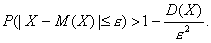

Теорема Чебышева: При достаточно большом числе независимых случайных величин Х₁, Х₂, Х₃, ..., Х_n, дисперсия каждой из которых не превышает одного и того же постоянного числа В, для произвольного сколько угодно малого числа e справедливо неравенство

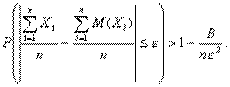
Из теоремы следует, что среднее арифметичес­кое случайных величин при возрастании их числа проявляет свойство устойчивости, т. е. стремится по вероятности к неслучайной величине, которой является среднее арифметическое математических ожиданий этих величин, т.е. вероятность отклонения по абсолютной величине среднего арифметического случайных величин от среднего арифметического их математических ожиданий меньше чем на e при неограниченном возрастании n стремится к 1, т.е. становится практически достоверным событием.

частный случай теоремы Чебышева:Пусть при n испытаниях наблюдаются n значений случайной величины X, имеющей математическое ожидание M(X) и дисперсию D(X). Полученные значения можно рассматривать как случайные величины Х₁, Х₂, Х₃, ..., Х_n,. Это следует понимать так. Серия из п испытаний проводится неоднократно. Поэтому в результате i-го испытания, i=l, 2, 3, ..., п, в каждой серии испытаний появится то или иное значение случайной величины X, не известное заранее. Следовательно, i-e значение x_i случайной величины, полученное в i-м испытании, изменяется случайным образом, если переходить от одной серии испытаний к другой. Таким образом, каждое значение x_iможно считать случайной величиной X_i .

Теорема Бернулли. Теорема Бернулли: Если вероятность события А в каждом из п независимых испытаний постоянна и равна р, то при достаточно большом п для произвольного e >0 справедливо неравенство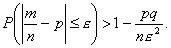

Переходя к пределу, имеем 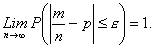Теорема Бернулли устанавливает связь между вероятностью появления события и его относительной частотой появления и позволяет при этом предсказать, какой примерно будет эта частота в п испытаниях. Из теоремы видно, что отношение т/п обладает свойством устойчивости при неограниченном росте числа испытаний.

Иногда (при решении практических задач) требуется оценить вероятность того, что отклонение числа т появления события в п испытаниях от ожидаемого результата пр не превысит определенного числа e. Для данной оценки неравенство переписывают в виде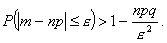

20.Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.