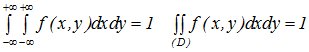Системы случайных величин. Функция распределения. Совместная плотность распределения.
Системоойслучайнвх величин (случайным вектором, многомерной случайной величиной)называется любая упорядоченная совокупность случайных величин Х ={X1, …, Xn}.
Случайные величины{X1, …, Xn}, входящие в систему могут быть как непрерывными, так и дискретными. Для наглядности рассмотрения пользуются геометрической интерпретацией; так систему двух случайных величин {X,Y} можно представить случайной точкой на плоскости с координатами X и Y, или случайным вектором, направленным из начала координат в точку (X,Y).
Свойства случайных величин не исчерпываются свойствами отдельных величин, входящих в систему и необходимы средства для описания характеристик систем случайных величин.
Функцией распределения (или совместной функцией распределения) системы случайных величин называется вероятность совместного выполнения неравенств X1<x1, …, Xn<xn:
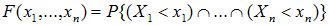 . (10.1)
. (10.1)
Для случая двумерной случайной величины:
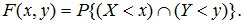 (10.2)
(10.2)
Геометрически функция распределения F(x,y) это вероятность попадания случайной точки (Х,У) в бесконечный квадрант с вершиной в точке (х,у), лежащей левее и ниже ее (рис. 10.1).
Свойства функции распределения.
1. Значения функции распределения удовлетворяют двойному неравенству:
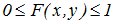 .
.
Доказательство этого свойства вытекает из определения функции распределения как вероятности: вероятность есть неотрицательное число, не превышающее 1.
2. Функция распределения F(x,y) есть неубывающая функция по каждому из аргументов т.е
х1 <х2 = > F(х1,у) £ F(х2, у)
у1< у2 = > F (х, у1) £ F (х,у2)
Доказательство этого свойства вытекает из того, что при увеличении какого-нибудь из аргументов (x,y) квадрант, заштрихованный на рис. 10.1, увеличивается; следовательно, вероятность попадания в него случайной точки (X,Y) уменьшаться не может.
3. Если хотя бы один из аргументов функции распределения обращается в -∞, то функция распределения равна 0:
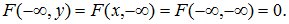 (10.3)
(10.3)
Доказательство. По определению
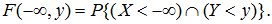
Событие 
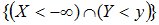 невозможное событие, т.к. невозможным является событие
невозможное событие, т.к. невозможным является событие 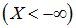 событие; тогда
событие; тогда
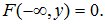
4. Если оба аргумента функции распределения F(x,y) равны +¥, то функция распределения равны 1.
Доказательство следует из определения функции распределения системы случайных величин:
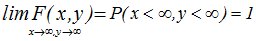 . (10.4)
. (10.4)
5.Если один из аргументов обращается в +∞, то функция распределения F(x,y) становится равной функции распределения случайной величины, соответствующей другому аргументу:
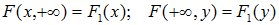 . (10.5)
. (10.5)
Доказательство. По определению функции распределения:
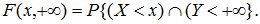
Событие (Y<+∞) является достоверным событием. Тогда
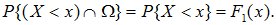
Точно так же доказывается, что
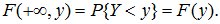
6. Вероятность попадания в прямоугольную область
P(a£X£b;d£U£g)=F(b,g)-F(b,d)-F(a,g)+F(a,d). (10.6)
Совместной плотностью вероятности или плотностью совместного распределения называется функция
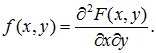 (10.11)
(10.11)
Плотность f(x,y) обладает следующими свойствами:
1. f(x,y)≥0;
2. 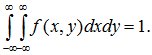
Геометрически совместная плотность f(x,y) системы двух случайных величин представляет собой некоторую поверхность распределения.
Аналогично вводится понятие элемента вероятности: 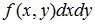 .
.
Элемент вероятности 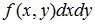 с точностью до бесконечно малых величин равен вероятности попадания случайной точки (X,Y) в элементарный прямоугольник ΔRxy, примыкающий к точке (x,y), с размерами Δx, Δy.
с точностью до бесконечно малых величин равен вероятности попадания случайной точки (X,Y) в элементарный прямоугольник ΔRxy, примыкающий к точке (x,y), с размерами Δx, Δy.
Аналогично тому, как было рассмотрено в случае одномерной случайной величины, определим вероятность попадания случайной точки (X,Y) в область D:
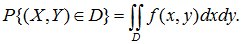 (10.12)
(10.12)
Функция распределения системы (X,Y) через совместную плотность определяется так:
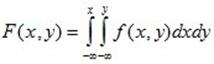 . (10.13)
. (10.13)
Совместная плотность распределения системы случайных величин (X,Y) позволяет вычислить одномерные законы распределения случайных величин X и Y :
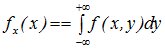 ;
; 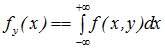 . (10.14)
. (10.14)
Одномерные плотности распределения составляющих системы случайных величин называют маргинальными плотностями распределения.
Условные плотностидля непрерывных составляющих X и Y определяются так
f(x/y) = f(x, y)/fу(y), fу (y)¹ 0; f(y/x) = f(x, y)/fх(x), fх (x)¹ 0. (10.17)
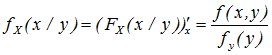 ;
;
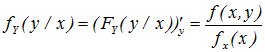 .
.
Условные плотности обладают всеми свойствами обычных плотностей:
1. Двумерная плотность вероятности неотрицательна 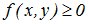
2. Условие нормировки